Păcatul judecății este considerat pe drept unul dintre cele mai distructive și...


Prelegerea nr. 60
6.21. Seria Fourier pentru funcții pare și impare.
Teorema: Pentru orice funcție pară, seria sa Fourier constă numai din cosinus.
Pentru orice funcție ciudată:  .
.
Dovada: Din definiția funcțiilor pare și impare rezultă că dacă ψ(x) este o funcție pară, atunci
 .
.
într-adevăr,

întrucât prin definiţia unei funcţii pare ψ(- x) = ψ(x).
În mod similar, putem demonstra că dacă ψ(x) este o funcție impară, atunci
Dacă o funcție impară ƒ(x) este extinsă într-o serie Fourier, atunci produsul ƒ(x) ·coskx este de asemenea o funcție impară, iar ƒ(x) ·sinkx este o funcție pară; prin urmare,
 (21)
(21)
adică seria Fourier a unei funcții impare conține „doar sinusuri”.
Dacă o funcție pară este extinsă într-o serie Fourier, atunci produsul ƒ(x)·sinkx este o funcție impară, iar ƒ(x)·coskx este o funcție pară, atunci:
 (22)
(22)
adică seria Fourier a unei funcții pare conține „doar cosinusuri”.
Formulele rezultate fac posibilă simplificarea calculelor la găsirea coeficienților Fourier în cazurile în care o funcție dată este pară sau impară și, de asemenea, obținerea Expansiunea seriei Fourier a unei funcții definite pe o parte a intervalului .
În multe sarcini funcția  este specificat în interval
este specificat în interval  . Este necesar să se reprezinte această funcție ca o sumă infinită de sinusuri și cosinusuri ale unghiurilor care sunt multipli ai numerelor naturale, de exemplu. este necesar să se extindă funcția într-o serie Fourier. De obicei, în astfel de cazuri se procedează după cum urmează.
. Este necesar să se reprezinte această funcție ca o sumă infinită de sinusuri și cosinusuri ale unghiurilor care sunt multipli ai numerelor naturale, de exemplu. este necesar să se extindă funcția într-o serie Fourier. De obicei, în astfel de cazuri se procedează după cum urmează.
Pentru a extinde o funcție dată în cosinus, funcția  determinat suplimentar în interval
determinat suplimentar în interval  într-un mod uniform, adică astfel încât în interval
într-un mod uniform, adică astfel încât în interval 
 . Atunci pentru funcția „extinsă” par sunt valabile toate argumentele din paragraful anterior și, în consecință, coeficienții Seria Fourier determinate prin formule
. Atunci pentru funcția „extinsă” par sunt valabile toate argumentele din paragraful anterior și, în consecință, coeficienții Seria Fourier determinate prin formule
 ,
,
Aceste formule, după cum vedem, includ valorile funcției  , specificat doar în interval
, specificat doar în interval  . Pentru a extinde o funcție
. Pentru a extinde o funcție  , specificat în interval
, specificat în interval  , prin sinusuri, este necesar să se definească în continuare această funcție în interval
, prin sinusuri, este necesar să se definească în continuare această funcție în interval  într-un mod ciudat, adică astfel încât în interval
într-un mod ciudat, adică astfel încât în interval 
 .
.
Apoi, calculul coeficienților seriei Fourier trebuie efectuat folosind formulele
 .
.
Teorema 1. O funcție dată pe un interval poate fi extinsă într-un număr infinit de moduri în serie trigonometrică Fourier, în special în cos sau sin.
Comentariu. Funcţie  , specificat în interval
, specificat în interval  poate fi definit în continuare în interval
poate fi definit în continuare în interval  în orice fel, și nu așa cum s-a făcut mai sus. Dar cu o redefinire arbitrară a funcției, expansiunea într-o serie Fourier va fi mai complexă decât cea obținută la extinderea în sinusuri sau cosinus.
în orice fel, și nu așa cum s-a făcut mai sus. Dar cu o redefinire arbitrară a funcției, expansiunea într-o serie Fourier va fi mai complexă decât cea obținută la extinderea în sinusuri sau cosinus.
Exemplu. Extindeți funcția într-o serie Fourier în cosinus  , specificat în interval
, specificat în interval  (Fig. 2a).
(Fig. 2a).
Soluţie. Să definim funcția  în interval
în interval  par (graficul este simetric în raport cu axa
par (graficul este simetric în raport cu axa  )
)

 ,
,

Deoarece  , Asta
, Asta
la 
 ,
,
la 


6.22. Serii Fourier pentru o funcție specificată pe un interval arbitrar
Până acum am luat în considerare o funcție definită în interval  , considerându-l periodic în afara acestui interval, cu punct
, considerându-l periodic în afara acestui interval, cu punct  .
.
Să luăm acum în considerare funcția  , a cărui perioadă este 2 l, adică
, a cărui perioadă este 2 l, adică  pe interval
pe interval  , și arătați că în acest caz funcția
, și arătați că în acest caz funcția  poate fi extins într-o serie Fourier.
poate fi extins într-o serie Fourier.
Să punem  , sau
, sau  . Apoi la schimbare
. Apoi la schimbare  de la – l la l variabilă nouă
de la – l la l variabilă nouă  variază de la
variază de la  la
la  şi deci funcţia
şi deci funcţia  poate fi considerată ca o funcţie specificată în intervalul de la
poate fi considerată ca o funcţie specificată în intervalul de la  la
la  și periodic în afara acestui interval, cu punct
și periodic în afara acestui interval, cu punct  .
.
Aşa,  .
.
Răspândindu-se  în seria Fourier, obținem
în seria Fourier, obținem
 ,
,

 .
.
Trecând la vechile variabile, de ex. crezând 
 , primim
, primim  ,
, Şi
Şi  .
.
Adică seria Fourier pentru funcție  , specificat în interval
, specificat în interval  , va arăta astfel:
, va arăta astfel:
 ,
,
 ,
,

 .
.
Dacă funcţia  este par, atunci formulele de determinare a coeficienților seriei Fourier sunt simplificate:
este par, atunci formulele de determinare a coeficienților seriei Fourier sunt simplificate:
 ,
,
 ,
,

 .
.
În cazul în care funcția  ciudat:
ciudat:
 ,
,
 ,
,

 .
.
Dacă funcţia  specificate în interval
specificate în interval  , apoi se poate continua în interval
, apoi se poate continua în interval  fie par, fie impar. În cazul continuării egale a funcției în interval
fie par, fie impar. În cazul continuării egale a funcției în interval 
 ,
,

 .
.
În cazul unei extensii impare a funcției în interval  coeficienții seriei Fourier se găsesc prin formule
coeficienții seriei Fourier se găsesc prin formule
 ,
,

 .
.
Exemplu. Extindeți funcția într-o serie Fourier

de-a lungul sinusurilor arcurilor multiple.
Soluţie. Graficul funcției date este prezentat în Fig. 3. Să continuăm funcția într-un mod ciudat (Fig. 4), adică. Vom realiza expansiunea din punct de vedere al sinusurilor.


Toate șansele 
 ,
,

Să introducem înlocuitorul  . Apoi la
. Apoi la  primim
primim  , la
, la  avem
avem  .
.
Astfel
 .
.
6.23. .Conceptul de extindere a seriei Fourier a funcțiilor neperiodice
Funcția definită în regiunea principală (-ℓ, ℓ) poate fi extinsă periodic dincolo de regiunea principală folosind relația funcțională ƒ(x+2 ℓ) = ƒ(x).
Pentru o funcție neperiodică ƒ(x) (-∞ φ(x)= Formula (2.18) va fi adevărată pe toată axa -∞< x< ∞ . Можно написать подобное разложение
для функции ƒ(x)= Formula (2.19) va fi adevărată numai pe un interval finit (-ℓ, ℓ), deoarece pe acest interval ƒ(x) și φ(x) coincid. Astfel, o funcție neperiodică poate fi extinsă într-o serie Fourier pe un interval finit. Multe procese care apar în natură și tehnologie tind să se repete la anumite intervale. Astfel de procese sunt numite periodice și sunt descrise matematic prin funcții periodice. Astfel de funcții includ păcat(x)
,
cos(x)
,
păcat(wx),
cos(wx)
. Suma a două funcții periodice, de exemplu, o funcție de forma ,
în general, nu mai este periodică. Dar se poate dovedi că dacă relația w 1
/
w 2
este un număr rațional, atunci această sumă este o funcție periodică. Cele mai simple procese periodice - oscilațiile armonice - sunt descrise prin funcții periodice păcat(wx)
Şi cos(wx).
Procesele periodice mai complexe sunt descrise de funcții compuse fie dintr-un număr finit, fie dintr-un număr infinit de termeni ai formei păcat(wx)
Şi cos(wx).
Să considerăm o serie funcțională de forma: Această serie se numește trigonometric; numere O 0
,
b 0
,
o 1
,
b 1
,O 2
,
b 2
…,
o n ,
b n ,…
sunt numite coeficienți serie trigonometrică. Seria (1) este adesea scrisă după cum urmează: Întrucât membrii seriei trigonometrice (2) au o perioadă comună Să presupunem că funcția f(x)
este suma acestei serii: În acest caz ei spun că funcția f(x)
este extins într-o serie trigonometrică. Presupunând că această serie converge uniform pe interval Se numesc coeficienții seriei determinate de aceste formule Coeficienții Fourier. Se numesc seriile trigonometrice (2), ai căror coeficienți sunt determinați folosind formulele Fourier (4). lângă Fourier, corespunzător funcției f(x).
Astfel, dacă o funcție periodică f(x)
este suma unei serii trigonometrice convergente, atunci această serie este seria sa Fourier. Formulele (4) arată că coeficienții Fourier pot fi calculați pentru orice integrabil pe interval Amintiți-vă că funcția f(x),
definite pe segment [
o;
b]
, se numește netedă pe bucăți dacă ea și derivata sa nu au mai mult de un număr finit de puncte de discontinuitate de primul fel. Următoarea teoremă oferă condiții suficiente pentru descompunerea unei funcții dintr-o serie Fourier. teorema lui Dirichlet.
Lasă Exemplul 1. Extindeți funcția într-o serie Fourier f(x)=
x, specificat pe interval Soluţie. Această funcție satisface condițiile Dirichlet și, prin urmare, poate fi extinsă într-o serie Fourier. Folosind formulele (4) și metoda de integrare pe părți Astfel, seria Fourier pentru funcția f(x)
are o privire. Extinderea seriei Fourier a funcțiilor pare și impare extinderea unei funcții dată pe un interval într-o serie în sinusuri sau cosinus Seria Fourier pentru o funcție cu o perioadă arbitrară Reprezentare complexă a seriei Fourier Seria Fourier în sistemele generale ortogonale de funcții Seria Fourier într-o sistem ortogonal Proprietate minimă a coeficienților Fourier Inegalitatea lui Bessel Egalitate Parseval Sisteme închise Completitudinea și caracterul închiderii sistemelor Expansiunea seriei Fourier a funcțiilor pare și impare O funcție f(x), definită pe intervalul \-1, unde I > 0, se numește chiar dacă graficul funcției pare este simetric față de axa ordonatelor. O funcție f(x), definită pe segmentul J), unde I > 0, se numește impară dacă graficul funcției impare este simetric față de origine. Exemplu. a) Funcția este pară pe intervalul |-jt, jt), deoarece pentru toate x e b) Funcția este impară, deoarece extinderea în serie Fourier a funcțiilor pare și impare este extinderea unei funcții dată pe un interval într-o serie în sinusuri sau Cosinusuri pentru o funcție cu o perioadă arbitrară Reprezentare complexă a seriei Fourier Serii Fourier pentru sistemele ortogonale generale de funcții Seria Fourier pentru un sistem ortogonal Proprietatea minimă a coeficienților Fourier Inegalitatea lui Bessel Egalitatea lui Parseval Sisteme închise Completitudinea și închiderea sistemelor c) Funcția. f(x)=x2-x, unde nu aparține nici funcțiilor pare, nici impare, întrucât Fie funcția f(x), care îndeplinește condițiile teoremei 1, să fie pară pe intervalul x|. Atunci pentru toată lumea adică. /(x) cos nx este o funcție pară, iar f(x) sinnx este una impară. Prin urmare, coeficienții Fourier ai unei funcții pare /(x) vor fi egali. Prin urmare, seria Fourier a unei funcții pare are forma f(x) sin х - o funcție pară. Prin urmare, vom avea Astfel, seria Fourier a unei funcții impare are forma Exemplul 1. Extindeți funcția 4 într-o serie Fourier pe intervalul -x ^ x ^ n Deoarece această funcție este pară și îndeplinește condițiile teoremei 1, atunci seria lui Fourier are forma Găsiți coeficienții Fourier. Avem Aplicând integrarea prin părți de două ori, obținem că Deci, seria Fourier a acestei funcții arată astfel: sau, în formă extinsă, Această egalitate este valabilă pentru orice x €, deoarece în punctele x = ±ir suma seria coincide cu valorile funcției f(x) = x2, deoarece graficele funcției f(x) = x și suma seriei rezultate sunt date în Fig. Comentariu. Această serie Fourier ne permite să găsim suma uneia dintre seriile numerice convergente, și anume, pentru x = 0 obținem acel Exemplu 2. Expandăm funcția /(x) = x într-o serie Fourier pe interval. 6. § 6. Expansiunea unei funcţii dată pe un interval într-o serie în sinusuri sau cosinusuri Fie dată pe interval o funcţie monotonă pe bucăţi mărginită /. Valorile acestei funcții pe intervalul 0| poate fi definit în continuare în diferite moduri. De exemplu, puteți defini o funcție / pe segmentul tc] astfel încât /. În acest caz ei spun că) „se extinde la segmentul 0] într-o manieră uniformă”; seria lui Fourier va conține numai cosinus. Dacă funcția /(x) este definită pe segmentul [-l-, mc] astfel încât /(, atunci obținem o funcție impară, și atunci se spune că / este „extins la segmentul [-*, 0] în un mod ciudat” în acest caz, seria Fourier va conține numai sinusuri. Astfel, fiecare funcție monotonă pe bucăți /(x) definită pe interval poate fi extinsă într-o serie Fourier atât în sinusuri, cât și în cosinus. Funcția poate fi extinsă într-o serie Fourier: a) prin cosinus; b) prin sinusuri. Aceasta dă și prin urmare, Geometric, această proprietate înseamnă că în cazul zonei umbrite în Fig. 10 zone sunt egale între ele. În special, pentru o funcție f(x) cu perioadă obținem la Expansiunea într-o serie Fourier de funcții pare și impare, extinderea unei funcții dată pe un interval într-o serie în sinusuri sau cosinusuri serie Fourier pentru o funcție cu o funcție arbitrară. perioada Notarea complexă a seriei Fourier Seria Fourier în funcții generale ale sistemelor ortogonale Seria Fourier într-un sistem ortogonal Proprietatea minimă a coeficienților Fourier Inegalitatea lui Bessel Egalitatea lui Parseval Sisteme închise Completitudinea și închiderea sistemelor Exemplul 2. Funcția x este periodică cu perioadă Datorită ciudățenie a acestei funcții, fără a calcula integrale, putem afirma că pentru orice Proprietatea dovedită, în special, arată că coeficienții Fourier ai unei funcții periodice f(x) cu o perioadă de 21 pot fi calculați folosind formulele în care a este un număr real arbitrar (de observat că funcțiile cos - și sin au perioada de 2/). Exemplul 3. Extindeți într-o serie Fourier o funcție dată pe un interval cu o perioadă de 2x (Fig. 11). 4 Să găsim coeficienții Fourier ai acestei funcții. Introducând formulele constatăm că pentru Prin urmare, seria Fourier va arăta astfel: În punctul x = jt (punct de discontinuitate de primul fel) avem §8. Înregistrarea complexă a seriei Fourier Această secțiune utilizează unele elemente de analiză complexă (vezi Capitolul XXX, unde toate acțiunile efectuate aici cu expresii complexe sunt strict justificate). Fie funcția f(x) să satisfacă condiții suficiente pentru extinderea într-o serie Fourier. Apoi pe segmentul x] poate fi reprezentat printr-o serie de forma Folosind formulele lui Euler Înlocuind aceste expresii în seria (1) în loc de cos πx și sin φx vom avea Să introducem următoarea notație Atunci seria (2) va lua forma Astfel, seria Fourier (1) este reprezentată în formă complexă (3). Să găsim expresii pentru coeficienți prin integrale. Avem În mod similar, găsim Formulele finale pentru с„, с_п și с pot fi scrise astfel: . . Coeficienții с„ se numesc coeficienți Fourier complecși ai funcției Pentru o funcție periodică cu o perioadă), forma complexă a seriei Fourier va lua forma în care coeficienții Cn sunt calculați folosind formulele de convergență a seriei (3 ) și (4) se înțelege astfel: seriile (3) și (4) se numesc convergente pentru valoare dată g, dacă există limite Exemplu. Extindeți funcția de perioadă într-o serie Fourier complexă Această funcție satisface condiții suficiente pentru extinderea într-o serie Fourier. Să găsim coeficienții Fourier complecși ai acestei funcții. Avem ca impar pentru n par sau, pe scurt. Înlocuind valorile), obținem în final. Notă că această serie poate fi scrisă și astfel: Serii Fourier pentru sistemele ortogonale generale de funcții 9.1. Sisteme ortogonale de funcții Să notăm prin mulțimea tuturor funcțiilor (reale) definite și integrabile pe intervalul [a, 6] cu un pătrat, adică acelea pentru care există o integrală, în special, toate funcțiile f(x) continue pe intervalul [a , 6], aparțin lui 6], iar valorile integralelor lor Lebesgue coincid cu valorile integralelor Riemann. Definiţie. Un sistem de funcții, unde, se numește ortogonal pe intervalul [a, b\, dacă Condiția (1) presupune, în special, că niciuna dintre funcții nu este identic zero. Integrala este înțeleasă în sensul Lebesgue. Seria Fourier într-un sistem ortogonal Să existe un sistem ortogonal de funcții în intervalul (a, 6) și să convergă seria (cj = const) pe acest interval către funcția f(x): Înmulțirea ambelor părți ale ultimei egalități prin - fix) și integrând peste x de la a la 6, datorită ortogonalității sistemului, obținem că această operație are, în general, un caracter pur formal. Totuși, în unele cazuri, de exemplu, când seria (4) converge uniform, toate funcțiile sunt continue și intervalul (a, 6) este finit, această operație este legală. Dar pentru noi acum este importantă interpretarea formală. Deci, să fie dată o funcție. Să formăm numerele c* folosind formula (5) și să scriem seria din partea dreaptă se numește seria Fourier a funcției f(x) în raport cu sistemul (^n(i)). numiți coeficienții Fourier ai funcției f(x) în raport cu acest sistem. Semnul ~ din formula (6) înseamnă doar că numerele Cn sunt legate de funcția f(x) prin formula (5) (nu se presupune că seria din dreapta converge deloc, cu atât mai puțin converge către funcția f (x)). Prin urmare, se pune firesc întrebarea: care sunt proprietățile acestei serii? În ce sens „reprezintă” funcția f(x)? 9.3. Convergenţă în medie Definiţie. O secvență converge către elementul ] în medie dacă norma este în spațiul Teorema 6. Dacă o secvență ) converge uniform, atunci converge în medie. Prin urmare, integrala (*) ia o valoare minimă la ak = sk Integrala se numește aproximarea pătratică medie a funcției /(x) printr-o combinație liniară a lui Tn(x). Astfel, aproximarea medie pătratică a funcției /\ ia o valoare minimă când. când Tn(x) este a 71-a sumă parțială a seriei Fourier a funcției /(x) asupra sistemului (. Fixând ak = sk, din (7) obținem Egalitatea (9) se numește identitatea Bessel. Deoarece stânga sa latura este nenegativă, atunci din aceasta rezultă inegalitatea lui Bessel Deoarece sunt aici în mod arbitrar, inegalitatea lui Bessel poate fi reprezentată într-o formă întărită, adică pentru orice funcție / seria de coeficienți Fourier pătrați ai acestei funcții într-un sistem ortonormal ) converge. . Deoarece sistemul este ortonormal pe intervalul [-x, m], atunci inegalitatea (10) tradusă în notația uzuală a seriei Fourier trigonometrice dă relația do care este valabilă pentru orice funcție /(x) cu un pătrat integrabil. Dacă f2(x) este integrabil, atunci, datorită condiției necesare pentru convergența seriei din partea stângă a inegalității (11), obținem că. Egalitatea lui Parseval Pentru unele sisteme (^„(x)), semnul inegalității din formula (10) poate fi înlocuit (pentru toate funcțiile f(x) 6 ×) cu un semn egal. Egalitatea rezultată se numește egalitatea Parseval-Steklov (condiția de completitudine). Identitatea lui Bessel (9) ne permite să scriem condiția (12) într-o formă echivalentă. Astfel, îndeplinirea condiției de completitudine înseamnă că sumele parțiale Sn(x) ale seriei Fourier ale funcției /(x) converg către funcția. /(x) în medie, adică conform normei de spațiu 6]. Definiţie. Un sistem ortonormal ( se numește complet în b2[ау b] dacă fiecare funcție poate fi aproximată în medie cu orice precizie printr-o combinație liniară a formei c suficient un număr mare termeni, adică dacă pentru orice funcție /(x) € b2[a, b\ și pentru orice e > 0 există un număr natural nq și numere a\, a2y..., astfel încât Nu Din raționamentul de mai sus rezultă teorema 7. Dacă prin ortonormalizare sistemul ) este complet în spațiu, seria Fourier a oricărei funcții / pentru acest sistem converge la f(x) în medie, adică conform normei Se poate demonstra că sistemul trigonometric este complet în spaţiu. Aceasta implică afirmaţia. Teorema 8. Dacă o funcție /o seria sa trigonometrică Fourier converge către ea în medie. 9.5. Sisteme închise. Completitudinea si inchiderea sistemelor Definitie. Un sistem ortonormal de funcții \ se numește închis dacă în spațiul Li\a, b) nu există o funcție diferită de zero ortogonală la toate funcțiile În spațiul L2\a, b\, conceptele de completitudine și închidere ale sistemelor ortonormale coincide. Exerciții 1. Extindeți funcția într-o serie Fourier în intervalul (-i-, x) 2. Extindeți funcția 3 într-o serie Fourier în intervalul (-tr, tr) 3. Extindeți funcția 4 într-o serie Fourier în intervalul (-tr, tr) într-o serie Fourier în intervalul (-jt, tr) funcția 5. Extindeți funcția f(x) = x + x într-o serie Fourier în intervalul (-jt, tr). 6. Extindeți funcția n într-o serie Fourier în intervalul (-jt, tr) 7. Extindeți funcția f(x) = sin2 x într-o serie Fourier în intervalul (-tr, x). 8. Extindeți funcția f(x) = y într-o serie Fourier în intervalul (-tr, jt) 9. Extindeți funcția f(x) = | sin x|. 10. Extindeți funcția f(x) = § într-o serie Fourier în intervalul (-π-, π). 11. Extindeți funcția f(x) = sin § într-o serie Fourier în intervalul (-tr, tr). 12. Extindeți funcția f(x) = n -2x, dată în intervalul (0, x), într-o serie Fourier, extinzând-o în intervalul (-x, 0): a) într-o manieră uniformă; b) într-un mod ciudat. 13. Extindeți funcția /(x) = x2, dată în intervalul (0, x), într-o serie Fourier în sinusuri. 14. Extindeți funcția /(x) = 3, dată în intervalul (-2,2), într-o serie Fourier. 15. Extindeți într-o serie Fourier funcția f(x) = |x|, dată în intervalul (-1,1). 16. Extindeți funcția f(x) = 2x, specificată în intervalul (0,1), într-o serie Fourier în sinusuri. Serii Fourier de funcții periodice cu perioada 2π.
Seria Fourier ne permite să studiem funcțiile periodice prin descompunerea lor în componente. Curenții și tensiunile alternative, deplasările, viteza și accelerația mecanismelor de manivelă și undele acustice sunt exemple practice tipice de utilizare a funcțiilor periodice în calculele inginerești. Expansiunea seriei Fourier se bazează pe presupunerea că toate având semnificație practică funcțiile din intervalul -π ≤x≤ π pot fi exprimate sub forma unor serii trigonometrice convergente (o serie este considerată convergentă dacă șirul sumelor parțiale compuse din termenii săi converge): Notație standard (=obișnuită) prin suma lui sinx și cosx f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+..., unde a o, a 1,a 2,...,b 1,b 2,.. sunt constante reale, i.e. Unde, pentru intervalul de la -π la π, coeficienții seriei Fourier sunt calculați folosind formulele: Se numesc coeficienții a o , a n și b n Coeficienții Fourier, iar dacă pot fi găsite, atunci se numește seria (1). lângă Fourier, corespunzător funcţiei f(x). Pentru seria (1), termenul (a 1 cosx+b 1 sinx) se numește primul sau armonică fundamentală, O altă modalitate de a scrie o serie este să folosiți relația acosx+bsinx=csin(x+α) f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n) Unde a o este o constantă, cu 1 =(a 1 2 +b 1 2) 1/2, cu n =(a n 2 +b n 2) 1/2 - amplitudinile diferitelor componente și este egal cu a n =arctg a n /b n. Pentru seria (1), termenul (a 1 cosx+b 1 sinx) sau c 1 sin(x+α 1) se numește primul sau armonică fundamentală,(a 2 cos2x+b 2 sin2x) sau c 2 sin(2x+α 2) se numește a doua armonicăși așa mai departe. Pentru a reprezenta cu acuratețe un semnal complex necesită de obicei un număr infinit de termeni. Cu toate acestea, în multe probleme practice este suficient să luăm în considerare doar primii termeni. Serii Fourier de funcții neperiodice cu perioada 2π.
Extinderea funcțiilor neperiodice. Dacă funcția f(x) este neperiodică, înseamnă că nu poate fi extinsă într-o serie Fourier pentru toate valorile lui x. Cu toate acestea, este posibil să se definească o serie Fourier reprezentând o funcție pe orice interval de lățime 2π. Având în vedere o funcție neperiodică, o nouă funcție poate fi construită prin selectarea valorilor lui f(x) într-un anumit interval și repetându-le în afara intervalului respectiv la intervale de 2π. Din moment ce caracteristică nouă este periodic cu o perioadă de 2π, poate fi extins într-o serie Fourier pentru toate valorile lui x. De exemplu, funcția f(x)=x nu este periodică. Cu toate acestea, dacă este necesar să o extindem într-o serie Fourier în intervalul de la o la 2π, atunci în afara acestui interval se construiește o funcție periodică cu o perioadă de 2π (după cum se arată în figura de mai jos). Pentru funcțiile neperiodice, cum ar fi f(x)=x, suma seriei Fourier este egală cu valoarea lui f(x) în toate punctele dintr-un interval dat, dar nu este egală cu f(x) pentru puncte în afara intervalului. Pentru a găsi seria Fourier a unei funcții neperiodice în domeniul 2π, se folosește aceeași formulă a coeficienților Fourier. Funcții pare și impare.
Ei spun că funcția y=f(x) chiar, dacă f(-x)=f(x) pentru toate valorile lui x. Graficele funcțiilor pare sunt întotdeauna simetrice față de axa y (adică sunt imagini în oglindă). Două exemple de funcții pare: y=x2 și y=cosx. Ei spun că funcția y=f(x) ciudat, dacă f(-x)=-f(x) pentru toate valorile lui x. Graficele funcțiilor impare sunt întotdeauna simetrice față de origine. Multe funcții nu sunt nici pare, nici impare. Expansiunea seriei Fourier în cosinus.
Seria Fourier a unei funcții periodice par f(x) cu perioada 2π conține numai termeni cosinus (adică nu conține termeni sinus) și poate include membru permanent. Prin urmare, unde sunt coeficienții seriei Fourier,
Seria Fourier a unei funcții periodice impare f(x) cu perioada 2π conține numai termeni cu sinusuri (adică nu conține termeni cu cosinus). Prin urmare, unde sunt coeficienții seriei Fourier, Seria Fourier la jumătate de ciclu.
Dacă o funcție este definită pentru un interval, să spunem de la 0 la π, și nu doar de la 0 la 2π, ea poate fi extinsă într-o serie numai în sinusuri sau numai în cosinus. Seria Fourier rezultată se numește lângă Fourier la jumătate de ciclu. Dacă vrei să obții descompunerea Fourier cu semiciclu prin cosinus funcțiile f(x) în intervalul de la 0 la π, atunci este necesar să se construiască o funcție periodică pară. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția pare este simetrică față de axa f(x), desenăm linia AB, așa cum se arată în Fig. de mai jos. Dacă presupunem că în afara intervalului considerat forma triunghiulară rezultată este periodică cu o perioadă de 2π, atunci graficul final arată astfel: în fig. de mai jos. Deoarece trebuie să obținem expansiunea Fourier în cosinus, ca și mai înainte, calculăm coeficienții Fourier a o și a n Dacă trebuie să obțineți Expansiune sinusală în semiciclu Fourier funcțiile f(x) în intervalul de la 0 la π, atunci este necesar să se construiască o funcție periodică impară. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția impară este simetrică față de origine, construim linia CD, așa cum se arată în Fig. Dacă presupunem că în afara intervalului considerat semnalul din dinte de ferăstrău rezultat este periodic cu o perioadă de 2π, atunci graficul final are forma prezentată în Fig. Deoarece trebuie să obținem expansiunea Fourier a semiciclului în termeni de sinusuri, ca și mai înainte, calculăm coeficientul Fourier. b Serii Fourier pentru un interval arbitrar.
Expansiunea unei funcții periodice cu perioada L. Funcția periodică f(x) se repetă pe măsură ce x crește cu L, adică. f(x+L)=f(x). Trecerea de la funcțiile considerate anterior cu o perioadă de 2π la funcțiile cu o perioadă de L este destul de simplă, deoarece se poate face folosind o schimbare de variabilă. Pentru a găsi seria Fourier a funcției f(x) în intervalul -L/2≤x≤L/2, introducem o nouă variabilă u astfel încât funcția f(x) să aibă o perioadă de 2π în raport cu u. Dacă u=2πx/L, atunci x=-L/2 pentru u=-π și x=L/2 pentru u=π. De asemenea, fie f(x)=f(Lu/2π)=F(u). Seria Fourier F(u) are forma (Limitele de integrare pot fi înlocuite cu orice interval de lungime L, de exemplu, de la 0 la L) Serii Fourier pe un semiciclu pentru funcțiile specificate în intervalul L≠2π.
Pentru substituția u=πх/L, intervalul de la x=0 la x=L corespunde intervalului de la u=0 la u=π. În consecință, funcția poate fi extinsă într-o serie numai în cosinus sau numai în sinusuri, i.e. V Seria Fourier la jumătate de ciclu. Expansiunea cosinusului în intervalul de la 0 la L are forma Seriile Fourier sunt o reprezentare a unei funcții arbitrare cu o anumită perioadă sub forma unei serii. ÎN vedere generală această decizie se numește descompunerea unui element pe bază ortogonală. Extinderea funcțiilor în seria Fourier este un instrument destul de puternic pentru rezolvarea diferitelor probleme datorită proprietăților acestei transformări în timpul integrării, diferențierii, precum și prin schimbarea expresiilor prin argument și convoluție. O persoană necunoscută matematica superioara, precum și cu lucrările omului de știință francez Fourier, cel mai probabil nu vor înțelege ce sunt aceste „serii” și pentru ce sunt necesare. Între timp, această transformare a devenit destul de integrată în viața noastră. Este folosit nu numai de matematicieni, ci și de fizicieni, chimiști, medici, astronomi, seismologi, oceanografi și mulți alții. De asemenea, să aruncăm o privire mai atentă asupra lucrărilor marelui om de știință francez care a făcut o descoperire care a fost înaintea timpului său. Serii Fourier sunt una dintre metode (împreună cu analize și altele). Acest proces are loc de fiecare dată când o persoană aude un sunet. Urechea noastră transformă automat particulele elementare într-un mediu elastic în rânduri (de-a lungul spectrului) de niveluri de volum succesive pentru tonuri de diferite înălțimi. Apoi, creierul transformă aceste date în sunete care ne sunt familiare. Toate acestea se întâmplă în afara dorinței sau conștiinței noastre, de la sine, dar pentru a înțelege aceste procese, va fi nevoie de câțiva ani pentru a studia matematica superioară. Transformarea Fourier poate fi efectuată folosind metode analitice, numerice și alte metode. Serii Fourier se referă la metoda numerică de descompunere a oricăror procese oscilatorii - de la maree oceanice și unde luminoase la cicluri de activitate solară (și alte obiecte astronomice). Folosind aceste tehnici matematice, puteți analiza funcții, reprezentând orice procese oscilatorii ca o serie de componente sinusoidale care se deplasează de la minim la maxim și înapoi. Transformata Fourier este o funcție care descrie faza și amplitudinea sinusoidelor corespunzătoare unei anumite frecvențe. Acest proces poate fi folosit pentru a rezolva ecuații foarte complexe care descriu procese dinamice, apărute sub influența energiei termice, luminoase sau electrice. De asemenea, seriile Fourier fac posibilă izolarea componentelor constante în semnale oscilatorii complexe, făcând posibilă interpretarea corectă a observațiilor experimentale obținute în medicină, chimie și astronomie. Părintele fondator al acestei teorii este matematicianul francez Jean Baptiste Joseph Fourier. Această transformare a fost ulterior numită după el. Inițial, omul de știință și-a folosit metoda pentru a studia și explica mecanismele conductivității termice - răspândirea căldurii în solide. Fourier a sugerat că distribuția neregulată inițială poate fi descompusă în sinusoide simple, fiecare dintre acestea având propria temperatură minimă și maximă, precum și propria sa fază. În acest caz, fiecare astfel de componentă va fi măsurată de la minim la maxim și înapoi. Funcția matematică care descrie vârfurile superioare și inferioare ale curbei, precum și faza fiecăreia dintre armonici, se numește transformată Fourier a expresiei distribuției temperaturii. Autorul teoriei a reunit functia generala distribuție, care este greu de descris matematic, la o serie foarte convenabilă de cosinus și sinus, care împreună dau distribuția originală. Contemporanii omului de știință – matematicieni de seamă de la începutul secolului al XIX-lea – nu au acceptat această teorie. Principala obiecție a fost afirmația lui Fourier că o funcție discontinuă, care descrie o linie dreaptă sau o curbă discontinuă, poate fi reprezentată ca o sumă de expresii sinusoidale care sunt continue. Ca exemplu, luați în considerare pasul Heaviside: valoarea sa este zero la stânga discontinuității și unu la dreapta. Această funcție descrie dependența curentului electric de o variabilă temporară atunci când circuitul este închis. Contemporanii teoriei de la acea vreme nu au întâlnit niciodată o situație similară în care o expresie discontinuă să fie descrisă printr-o combinație de funcții continue, obișnuite, cum ar fi exponențial, sinus, liniar sau pătratic. La urma urmei, dacă matematicianul a avut dreptate în afirmațiile sale, atunci prin însumarea seriei infinite trigonometrice Fourier, se poate obține o reprezentare precisă a expresiei pasului, chiar dacă are mulți pași similari. La începutul secolului al XIX-lea, o astfel de afirmație părea absurdă. Dar, în ciuda tuturor îndoielilor, mulți matematicieni și-au extins sfera studiului lor asupra acestui fenomen, ducându-l dincolo de studiul conductivității termice. Cu toate acestea, majoritatea oamenilor de știință au continuat să fie chinuiți de întrebarea: „Poate suma unei serii sinusoidale să convergă către valoarea exactă a funcției discontinue?” Problema convergenței se pune ori de câte ori este necesar să se însumeze serii infinite de numere. Pentru a înțelege acest fenomen, luați în considerare un exemplu clasic. Vei putea vreodată să ajungi la perete dacă fiecare pas următor este jumătate din dimensiunea celui precedent? Să presupunem că ești la doi metri de țintă, primul pas te duce până la jumătatea drumului, următorul te duce până la marcajul de trei sferturi, iar după al cincilea vei fi parcurs aproape 97 la sută din drum. Cu toate acestea, indiferent de câți pași ai face, nu îți vei atinge scopul propus într-un sens strict matematic. Folosind calcule numerice, se poate dovedi că în cele din urmă este posibil să se apropie cât mai mult de o anumită distanță. Această dovadă este echivalentă cu demonstrarea că suma unei jumătăți, a unui sfert etc. va tinde spre unitate. Această problemă a fost ridicată din nou la sfârșitul secolului al XIX-lea, când au încercat să folosească seria Fourier pentru a prezice intensitatea mareelor. În acest moment, Lordul Kelvin a inventat un instrument, care era un dispozitiv de calcul analogic care permitea marinarilor militari și marini comerciali să urmărească acest lucru. fenomen natural. Acest mecanism a determinat seturi de faze și amplitudini dintr-un tabel de înălțimi ale mareelor și puncte de timp corespunzătoare, măsurate cu atenție într-un anumit port pe tot parcursul anului. Fiecare parametru a fost o componentă sinusoidală a expresiei înălțimii mareei și a fost una dintre componentele regulate. Măsurătorile au fost introduse în instrumentul de calcul al lui Lord Kelvin, care a sintetizat o curbă care a prezis înălțimea apei în funcție de timp pentru anul următor. Foarte curând au fost trasate curbe similare pentru toate porturile lumii. La acea vreme, părea evident că un predictor de undă mare cu un număr mare de elemente de numărare ar putea calcula un număr mare de faze și amplitudini și astfel să ofere predicții mai precise. Cu toate acestea, s-a dovedit că acest model nu este observat în cazurile în care expresia mareelor care ar trebui sintetizată conținea un salt ascuțit, adică era discontinuu. Dacă datele dintr-un tabel de momente de timp sunt introduse în dispozitiv, acesta calculează mai mulți coeficienți Fourier. Funcția inițială este restabilită datorită componentelor sinusoidale (în conformitate cu coeficienții aflați). Discrepanța dintre expresia originală și cea reconstruită poate fi măsurată în orice punct. Când se efectuează calcule și comparații repetate, este clar că valoarea celei mai mari erori nu scade. Cu toate acestea, ele sunt localizate în regiunea corespunzătoare punctului de discontinuitate, iar în orice alt punct tind spre zero. În 1899, acest rezultat a fost confirmat teoretic de Joshua Willard Gibbs de la Universitatea Yale. Analiza Fourier nu este aplicabilă expresiilor care conțin un număr infinit de vârfuri într-un anumit interval. În general, seria Fourier, dacă funcția inițială este reprezentată de rezultatul realului dimensiunea fizică, converg mereu. Întrebările despre convergența acestui proces pentru clase specifice de funcții au condus la apariția de noi ramuri în matematică, de exemplu, teoria funcțiilor generalizate. Ea este asociată cu nume precum L. Schwartz, J. Mikusinski și J. Temple. În cadrul acestei teorii, a fost creată o bază teoretică clară și precisă pentru expresii precum funcția deltei Dirac (descrie o regiune dintr-o singură zonă concentrată într-o vecinătate infinitezimală a unui punct) și „pasul” Heaviside. Datorită acestei lucrări, seria Fourier a devenit aplicabilă pentru rezolvarea ecuațiilor și a problemelor care implică concepte intuitive: sarcină punctiformă, masă punctuală, dipoli magnetici și sarcină concentrată pe un fascicul. Seria Fourier, în conformitate cu principiile interferenței, încep cu descompunerea formelor complexe în altele mai simple. De exemplu, o modificare a fluxului de căldură se explică prin trecerea sa prin diferite obstacole din material termoizolant de formă neregulată sau o modificare a suprafeței pământului - un cutremur, o schimbare a orbitei corp ceresc- influența planetelor. De regulă, astfel de ecuații care descriu sisteme clasice simple pot fi rezolvate cu ușurință pentru fiecare val individual. Fourier a arătat că soluțiile simple pot fi, de asemenea, însumate pentru a produce soluții la probleme mai complexe. În termeni matematici, seriile Fourier sunt o tehnică de reprezentare a unei expresii ca o sumă de armonici - cosinus și sinus. Prin urmare, această analiză este cunoscută și sub denumirea de „analiza armonică”. Înainte de crearea tehnologiei informatice, tehnica Fourier a fost cea mai bună armăîn arsenalul oamenilor de știință atunci când lucrează cu natura ondulatorie a lumii noastre. Seria Fourier în formă complexă face posibilă rezolvarea nu numai a problemelor simple care sunt susceptibile de aplicarea directă a legilor mecanicii lui Newton, ci și ecuații fundamentale. Majoritatea descoperirilor științei newtoniene din secolul al XIX-lea au fost posibile numai prin tehnica lui Fourier. Odată cu dezvoltarea computerelor, transformatele Fourier s-au ridicat la un nivel calitativ nou nivel. Această tehnică este ferm stabilită în aproape toate domeniile științei și tehnologiei. Un exemplu este audio și video digital. Implementarea sa a devenit posibilă doar datorită unei teorii dezvoltate de un matematician francez la începutul secolului al XIX-lea. Astfel, seria Fourier în formă complexă a făcut posibilă realizarea unei descoperiri în studiu spațiul cosmic. În plus, a influențat studiul fizicii materialelor semiconductoare și a plasmei, acustica microundelor, oceanografie, radar și seismologie. În matematică, o serie Fourier este o modalitate de a reprezenta funcții complexe arbitrare ca o sumă a celor mai simple. În cazuri generale, numărul de astfel de expresii poate fi infinit. Mai mult, cu cât numărul lor este luat în considerare în calcul, cu atât rezultatul final este mai precis. Cel mai adesea folosit ca protozoare funcții trigonometrice cosinus sau sinus. În acest caz, seriile Fourier se numesc trigonometrice, iar soluția unor astfel de expresii se numește expansiune armonică. Această metodă joacă un rol important în matematică. În primul rând, seria trigonometrică oferă un mijloc de înfățișare și, de asemenea, studierea funcțiilor este principalul aparat al teoriei. În plus, vă permite să rezolvați o serie de probleme din fizica matematică. În cele din urmă, această teorie a contribuit la dezvoltarea și a adus la viață o serie de ramuri foarte importante ale științei matematice (teoria integralelor, teoria funcțiilor periodice). În plus, a servit drept punct de plecare pentru dezvoltarea următoarelor funcții ale unei variabile reale și, de asemenea, a pus bazele analizei armonice. (2.18)
(2.18) (2.19)
(2.19)3.2. Seria trigonometrică. Coeficienții Fourier
 .
(2)
.
(2) , atunci suma seriei, dacă converge, este și o funcție periodică cu perioadă
, atunci suma seriei, dacă converge, este și o funcție periodică cu perioadă  .
. .
(3)
.
(3) , puteți determina coeficienții săi folosind formulele:
, puteți determina coeficienții săi folosind formulele: ,
,  ,
, .
(4)
.
(4)3.3. Convergența seriei Fourier

 -functie periodica, i.e. Pentru o astfel de funcție se poate construi întotdeauna o serie Fourier. Dar această serie va converge către funcție f(x)
si in ce conditii?
-functie periodica, i.e. Pentru o astfel de funcție se poate construi întotdeauna o serie Fourier. Dar această serie va converge către funcție f(x)
si in ce conditii? -functie periodica f(x)
este netedă pe bucăți
-functie periodica f(x)
este netedă pe bucăți  . Apoi seria lui Fourier converge către f(x)
în fiecare dintre punctele sale de continuitate şi la valoare 0,5(f(x+0)+
f(x-0))
la punctul de rupere.
. Apoi seria lui Fourier converge către f(x)
în fiecare dintre punctele sale de continuitate şi la valoare 0,5(f(x+0)+
f(x-0))
la punctul de rupere. .
. , găsim coeficienții Fourier:
, găsim coeficienții Fourier:



























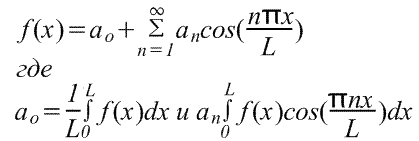
Omul și transformarea Fourier

Mai multe despre transformata Fourier

Context istoric
Principiul transformării și punctele de vedere ale contemporanilor

Ce i-a derutat pe matematicienii francezi cu privire la teoria lui Fourier?
Convergența seriei Fourier: un exemplu

Problema convergenței: a doua venire sau instrumentul lordului Kelvin
Ce se întâmplă dacă procesul este perturbat de o funcție discontinuă?

Convergența seriilor Fourier și dezvoltarea matematicii în general
Metoda Fourier
Seria Fourier - o tehnică ideală înainte de „era computerului”

Seria Fourier azi
Seria Fourier trigonometrică