Soluție seria Fourier. Seria Fourier în exemple și probleme

Serii Fourier de funcții periodice cu perioada 2π.

Seria Fourier ne permite să studiem funcțiile periodice prin descompunerea lor în componente. Curenții și tensiunile alternative, deplasările, viteza și accelerația mecanismelor de manivelă și undele acustice sunt exemple practice tipice de utilizare a funcțiilor periodice în calculele inginerești.

Expansiunea seriei Fourier se bazează pe presupunerea că toate având semnificație practică funcțiile din intervalul -π ≤x≤ π pot fi exprimate sub forma unor serii trigonometrice convergente (o serie este considerată convergentă dacă șirul sumelor parțiale compuse din termenii săi converge):

Notație standard (=obișnuită) prin suma lui sinx și cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

unde a o, a 1,a 2,...,b 1,b 2,.. sunt constante reale, i.e.

Unde, pentru intervalul de la -π la π, coeficienții seriei Fourier sunt calculați folosind formulele:

Coeficienții a o , a n și b n se numesc coeficienți Fourier, iar dacă pot fi găsiți, atunci seria (1) se numește lângă Fourier, corespunzătoare funcției f(x). Pentru seria (1), termenul (a 1 cosx+b 1 sinx) se numește prima armonică sau armonică fundamentală,

O altă modalitate de a scrie o serie este să folosiți relația acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Unde a o este o constantă, cu 1 =(a 1 2 +b 1 2) 1/2, cu n =(a n 2 +b n 2) 1/2 - amplitudinile diferitelor componente și este egal cu a n =arctg a n /b n.

Pentru seria (1), termenul (a 1 cosx+b 1 sinx) sau c 1 sin(x+α 1) se numește prima armonică sau armonică fundamentală, (a 2 cos2x+b 2 sin2x) sau c 2 sin(2x). +α 2) numită a doua armonică și așa mai departe.

Pentru a reprezenta cu acuratețe un semnal complex necesită de obicei un număr infinit de termeni. Cu toate acestea, în multe probleme practice este suficient să luăm în considerare doar primii termeni.

Serii Fourier de funcții neperiodice cu perioada 2π.

Extinderea funcțiilor neperiodice.

Dacă funcția f(x) este neperiodică, înseamnă că nu poate fi extinsă într-o serie Fourier pentru toate valorile lui x. Cu toate acestea, este posibil să se definească o serie Fourier reprezentând o funcție pe orice interval de lățime 2π.

Având în vedere o funcție neperiodică, o nouă funcție poate fi construită prin selectarea valorilor lui f(x) într-un anumit interval și repetându-le în afara intervalului respectiv la intervale de 2π. Din moment ce caracteristică nouă este periodic cu o perioadă de 2π, poate fi extins într-o serie Fourier pentru toate valorile lui x. De exemplu, funcția f(x)=x nu este periodică. Cu toate acestea, dacă este necesar să o extindem într-o serie Fourier în intervalul de la o la 2π, atunci în afara acestui interval se construiește o funcție periodică cu o perioadă de 2π (după cum se arată în figura de mai jos).

Pentru funcțiile neperiodice, cum ar fi f(x)=x, suma seriei Fourier este egală cu valoarea lui f(x) în toate punctele dintr-un interval dat, dar nu este egală cu f(x) pentru puncte în afara intervalului. Pentru a găsi seria Fourier a unei funcții neperiodice în domeniul 2π, se folosește aceeași formulă a coeficienților Fourier.

Funcții pare și impare.

Se spune că o funcție y=f(x) este chiar dacă f(-x)=f(x) pentru toate valorile lui x. Graficele funcțiilor pare sunt întotdeauna simetrice față de axa y (adică sunt imagini în oglindă). Două exemple de funcții pare: y=x2 și y=cosx.

Se spune că o funcție y=f(x) este impară dacă f(-x)=-f(x) pentru toate valorile lui x. Graficele funcțiilor impare sunt întotdeauna simetrice față de origine.

Multe funcții nu sunt nici pare, nici impare.

Expansiunea seriei Fourier în cosinus.

Seria Fourier a unei funcții periodice par f(x) cu perioada 2π conține numai termeni cosinus (adică nu conține termeni sinus) și poate include membru permanent. Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier a unei funcții periodice impare f(x) cu perioada 2π conține numai termeni cu sinusuri (adică nu conține termeni cu cosinus).

Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier la jumătate de ciclu.

Dacă o funcție este definită pentru un interval, să spunem de la 0 la π, și nu doar de la 0 la 2π, ea poate fi extinsă într-o serie numai în sinusuri sau numai în cosinus. Seria Fourier rezultată se numește seria Fourier cu semiciclu.

Dacă doriți să obțineți o expansiune Fourier pe jumătate de ciclu în termeni de cosinus ale funcției f(x) în intervalul de la 0 la π, atunci trebuie să construiți un par functie periodica. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția pare este simetrică față de axa f(x), desenăm linia AB, așa cum se arată în Fig. de mai jos. Dacă presupunem că în afara intervalului considerat forma triunghiulară rezultată este periodică cu o perioadă de 2π, atunci graficul final arată astfel: în fig. de mai jos. Deoarece trebuie să obținem expansiunea Fourier în cosinus, ca și mai înainte, calculăm coeficienții Fourier a o și a n

Dacă doriți să obțineți o expansiune Fourier pe jumătate de ciclu în termeni de sinus ale funcției f(x) în intervalul de la 0 la π, atunci trebuie să construiți o funcție periodică impară. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția impară este simetrică față de origine, construim linia CD, așa cum se arată în Fig. Dacă presupunem că în afara intervalului considerat semnalul din dinte de ferăstrău rezultat este periodic cu o perioadă de 2π, atunci graficul final are forma prezentată în Fig. Deoarece trebuie să obținem expansiunea Fourier a semiciclului în termeni de sinusuri, ca și mai înainte, calculăm coeficientul Fourier. b

Serii Fourier pentru un interval arbitrar.

Expansiunea unei funcții periodice cu perioada L.

Funcția periodică f(x) se repetă pe măsură ce x crește cu L, adică. f(x+L)=f(x). Trecerea de la funcțiile considerate anterior cu o perioadă de 2π la funcțiile cu o perioadă de L este destul de simplă, deoarece se poate face folosind o schimbare de variabilă.

Pentru a găsi seria Fourier a funcției f(x) în intervalul -L/2≤x≤L/2, introducem o nouă variabilă u astfel încât funcția f(x) să aibă o perioadă de 2π în raport cu u. Dacă u=2πx/L, atunci x=-L/2 pentru u=-π și x=L/2 pentru u=π. De asemenea, fie f(x)=f(Lu/2π)=F(u). Seria Fourier F(u) are forma

(Limitele de integrare pot fi înlocuite cu orice interval de lungime L, de exemplu, de la 0 la L)

Serii Fourier pe un semiciclu pentru funcțiile specificate în intervalul L≠2π.

Pentru substituția u=πх/L, intervalul de la x=0 la x=L corespunde intervalului de la u=0 la u=π. În consecință, funcția poate fi extinsă într-o serie numai în cosinus sau numai în sinusuri, i.e. într-o serie Fourier la jumătate de ciclu.

Expansiunea cosinusului în intervalul de la 0 la L are forma

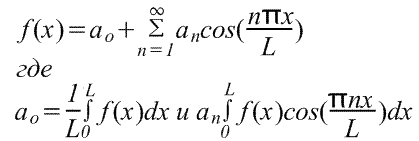
Seria Fourier a unei funcții periodice par f(x) cu perioada 2p conține numai termeni cu cosinus (adică nu conține termeni cu sinusuri) și poate include un termen constant. Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier a unei funcții periodice impare f (x) cu perioada 2p conține numai termeni cu sinusuri (adică nu conține termeni cu cosinus).

Prin urmare,

unde sunt coeficienții seriei Fourier,

Dacă o funcție este definită pentru un interval, să spunem de la 0 la p, și nu doar de la 0 la 2p, ea poate fi extinsă într-o serie numai în sinusuri sau numai în cosinus. Seria Fourier rezultată se numește seria Fourier cu semiciclu.

Dacă doriți să obțineți o expansiune Fourier în jumătate de ciclu a cosinusurilor funcției f (x) în intervalul de la 0 la p, atunci trebuie să construiți o funcție periodică pară. În fig. Mai jos este funcția f (x) = x, construită pe intervalul de la x = 0 la x = p. Deoarece funcția pare este simetrică față de axa f (x), desenăm linia AB, așa cum se arată în Fig. de mai jos. Dacă presupunem că în afara intervalului considerat forma triunghiulară rezultată este periodică cu o perioadă de 2p, atunci graficul final arată astfel: în fig. de mai jos. Deoarece trebuie să obținem expansiunea Fourier în cosinus, ca și mai înainte, calculăm coeficienții Fourier a o și a n

Dacă doriți să obțineți expansiunea Fourier pe o jumătate de ciclu în termenii sinusurilor funcției f (x) în intervalul de la 0 la p, atunci trebuie să construiți o funcție periodică impară. În fig. Mai jos este funcția f (x) =x, construită pe intervalul de la x=0 la x=p. Deoarece funcția impară este simetrică față de origine, construim linia CD, așa cum se arată în Fig.

Dacă presupunem că în afara intervalului considerat semnalul din dinte de ferăstrău rezultat este periodic cu o perioadă de 2p, atunci graficul final are forma prezentată în Fig. Deoarece trebuie să obținem expansiunea Fourier a semiciclului în termeni de sinusuri, ca și mai înainte, calculăm coeficientul Fourier. b

Cum se inserează formule matematice pe un site web?

Dacă vreodată trebuie să adăugați una sau două formule matematice pe o pagină web, atunci cel mai simplu mod de a face acest lucru este descris în articol: formulele matematice sunt ușor de inserat pe site sub formă de imagini care sunt generate automat de Wolfram Alpha . Pe lângă simplitate, asta metoda universala va ajuta la îmbunătățirea vizibilității site-ului web în motoarele de căutare. Funcționează de mult timp (și cred că va funcționa pentru totdeauna), dar este deja depășit din punct de vedere moral.

Dacă utilizați în mod constant formule matematice pe site-ul dvs., atunci vă recomand să utilizați MathJax - o bibliotecă JavaScript specială care afișează notatie matematicaîn browserele web care utilizează markup MathML, LaTeX sau ASCIIMathML.

Există două moduri de a începe să utilizați MathJax: (1) folosind un cod simplu, puteți conecta rapid un script MathJax la site-ul dvs., care va fi încărcat automat de pe un server la distanță la momentul potrivit (lista de servere); (2) descărcați scriptul MathJax de pe un server la distanță pe serverul dvs. și conectați-l la toate paginile site-ului dvs. A doua metodă - mai complexă și consumatoare de timp - va grăbi încărcarea paginilor site-ului dvs., iar dacă serverul MathJax părinte devine temporar indisponibil dintr-un motiv oarecare, acest lucru nu vă va afecta în niciun fel propriul site. În ciuda acestor avantaje, am ales prima metodă deoarece este mai simplă, mai rapidă și nu necesită abilități tehnice. Urmează-mi exemplul și în doar 5 minute vei putea folosi toate funcțiile MathJax de pe site-ul tău.

Puteți conecta scriptul de bibliotecă MathJax de la un server la distanță folosind două opțiuni de cod preluate de pe site-ul principal MathJax sau de pe pagina de documentație:

Una dintre aceste opțiuni de cod trebuie să fie copiată și lipită în codul paginii dvs. web, de preferință între etichete și/sau imediat după etichetă. Conform primei opțiuni, MathJax se încarcă mai repede și încetinește pagina mai puțin. Dar a doua opțiune monitorizează și încarcă automat cele mai recente versiuni de MathJax. Dacă introduceți primul cod, acesta va trebui actualizat periodic. Dacă introduceți al doilea cod, paginile se vor încărca mai lent, dar nu va trebui să monitorizați în mod constant actualizările MathJax.

Cel mai simplu mod de a conecta MathJax este în Blogger sau WordPress: în panoul de control al site-ului, adăugați un widget conceput pentru a insera cod JavaScript terță parte, copiați prima sau a doua versiune a codului de descărcare prezentat mai sus în el și plasați widgetul mai aproape la începutul șablonului (apropo, acest lucru nu este deloc necesar, deoarece scriptul MathJax este încărcat asincron). Asta e tot. Acum aflați sintaxa de marcare a MathML, LaTeX și ASCIIMathML și sunteți gata să inserați formule matematice în paginile web ale site-ului dvs.

Orice fractal este construit după o anumită regulă, care este aplicată în mod constant de un număr nelimitat de ori. Fiecare astfel de timp se numește iterație.

Algoritmul iterativ pentru construirea unui burete Menger este destul de simplu: cubul original cu latura 1 este împărțit de planuri paralele cu fețele sale în 27 de cuburi egale. Un cub central și 6 cuburi adiacente acestuia de-a lungul fețelor sunt îndepărtate din el. Rezultatul este un set format din restul de 20 de cuburi mai mici. Făcând același lucru cu fiecare dintre aceste cuburi, obținem un set format din 400 de cuburi mai mici. Continuând acest proces la nesfârșit, obținem un burete Menger.

1 MINISTERUL EDUCAȚIEI ȘI ȘTIINȚEI AL UNIVERSITĂȚII DE STAT RF NOVOSIBIRSK FACULTATEA DE FIZICĂ R. K. Belkheeva SERIA FOURIER ÎN EXEMPLE ȘI PROBLEME Manual Novosibirsk 211

2 UDC BBK V161 B44 B44 Belkheeva R.K Seria Fourier în exemple și probleme: Manual / Novosibirsk. stat univ. Novosibirsk, s. ISBN B manual sunt prezentate informații de bază despre seria Fourier, sunt date exemple pentru fiecare subiect studiat. Este analizat în detaliu un exemplu de aplicare a metodei Fourier pentru rezolvarea problemei vibrațiilor transversale ale unei coarde. Este furnizat material ilustrativ. Există sarcini pentru soluții independente. Destinat studenților și profesorilor Facultății de Fizică din NSU. Publicat prin hotărâre a comisiei metodologice a Facultății de Fizică a UNS. Revizor: Dr. Phys.-Math. Sci. V. A. Aleksandrov Manualul a fost pregătit ca parte a implementării Programului de dezvoltare NRU-NSU pe ani. ISBN din Novosibirsk universitate de stat, 211 c Belkheeva R.K., 211

3 1. Extinderea unei funcții 2π-periodice într-o serie Fourier Definiție. Seria Fourier a funcției f(x) este seria funcțională a 2 + (a n cosnx + b n sin nx), (1) unde coeficienții a n, b n sunt calculați folosind formulele: a n = 1 π b n = 1 π f (x) cosnxdx, n = , 1,..., (2) f(x) sin nxdx, n = 1, 2,.... (3) Formulele (2) (3) se numesc formule Euler Fourier. Faptul că funcția f(x) corespunde seriei Fourier (1) se scrie ca formula f(x) a 2 + (a n cosnx + b n sin nx) (4) și spunem că partea dreaptă a formulei ( 4) este o serie formală funcție Fourier f(x). Cu alte cuvinte, formula (4) înseamnă doar că coeficienții a n, b n au fost găsiți folosind formulele (2), (3). 3

4 Definiție. O funcție 2π-periodică f(x) se numește netedă pe bucăți dacă există un număr finit de puncte = x în intervalul [, π]< x 1 . Рассмотрим два условия: а) f(l x) = f(x); б) f(l + x) = f(x), x [, l/2]. С геометрической точки зрения условие (а) означает, что график функции f(x) симметричен относительно вертикальной прямой x = l/2, а условие (б) что график f(x) центрально симметричен относительно точки (l/2;) на оси абсцисс. Тогда справедливы следующие утверждения: 1) если функция f(x) четная и выполнено условие (а), то b 1 = b 2 = b 3 =... =, a 1 = a 3 = a 5 =... = ; 2) если функция f(x) четная и выполнено условие (б), то b 1 = b 2 = b 3 =... =, a = a 2 = a 4 =... = ; 3) если функция f(x) нечетная и выполнено условие (а), то a = a 1 = a 2 =... =, b 2 = b 4 = b 6 =... = ; 4) если функция f(x) нечетная и выполнено условие (б), то a = a 1 = a 2 =... =, b 1 = b 3 = b 5 =... =. ЗАДАЧИ В задачах 1 7 нарисуйте графики и найдите ряды Фурье для функций, { предполагая, что они имеют период 2π:, если < x a cosx + a2 В задачах найдите ряды Фурье в комплексной форме для функций. 26. f(x) = sgn x, π < x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Teorema egalității lui Lyapunov (egalitatea lui Lyapunov). Fie funcția f: [, π] R astfel încât f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n = 2 π f(x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. Prin urmare, egalitatea Lyapunov pentru funcția f(x) ia forma: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. Din ultima egalitate pentru a π găsim sin 2 na n 2 = a(π a) 2 Punând a = π 2, obținem sin2 na = 1 pentru n = 2k 1 și sin 2 na = pentru n = 2k. Prin urmare, k=1 1 (2k 1) 2 = = π2 8. EXEMPLU 14. Să scriem egalitatea lui Lyapunov pentru funcția f(x) = x cosx, x [, π] și să o folosim pentru a găsi suma numărului serie (4n 2 + 1) 2 (4n 2 1) 4. 1 π Soluție. Calculele directe dau = π π f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π 1 4π cos 2xdx =

49 Deoarece f(x) este o funcție pară, atunci pentru tot n avem b n =, a n = 2 π = 1 π 1 = π(n + 1) = f(x) cosnxdx = 2 π 1 cos(n + 1 )x π (n + 1) 2 x cosxcosnxdx = x (cos(n + 1)x + cos(n 1)x) dx = 1 π sin(n + 1)xdx sin(n 1)xdx = π(n 1) π π 1 + cos(n 1)x = π(n 1) 2 1 (= (1) (n+1) 1) 1 (+ (1) (n+1) 1) = π(n + 1) 2 π(n 1) 2 () = (1)(n+1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1)(n+1) 1 n k π (n 2 1) = π (4k 2 1) 2 dacă n = 2k, 2 dacă n = 2k + 1. Coeficientul a 1 trebuie calculat separat, deoarece în formula generală pentru n = 1 numitorul fracției merge la zero. = 1 π a 1 = 2 π f(x) cosxdx = 2 π x(1 + cos 2x)dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.

50 Astfel, egalitatea lui Lyapunov pentru funcția f(x) are forma: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π, de unde găsim suma seriei numerice (4n 2). + 1) 2 (4n 2 1) = π π PROBLEME 32. Scrieți egalitatea lui Lyapunov pentru funcția ( x f(x) = 2 πx, dacă x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) = π sin 2απ 2απ = 2sin2 απ α 2 π 2 Răspunsuri + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f(x)g(x) dx= c n d n, unde c n este coeficientul Fourier 2π al funcției f(x), iar d n este funcțiile coeficientului Fourier g(x). 6. Diferențierea seriei Fourier Fie f: R R o funcție 2π-periodică continuu derivabilă. Seria lui Fourier are forma: f(x) = a 2 + (a n cos nx + b n sin nx). Derivata f (x) a acestei functii va fi o functie continua si 2π-periodica, pentru care putem scrie o serie formala Fourier: f (x) a 2 + (a n cos nx + b n sin nx), unde a, a n , b n, n = 1 , 2,... Coeficienții Fourier ai funcției f (x). 51

52 Teoremă (cu privire la diferențierea termen cu termen a seriei Fourier). Conform ipotezelor de mai sus, egalitățile a =, a n = nb n, b n = na n, n 1 sunt valabile. Să demonstrăm că dacă condiția f(x)dx = este îndeplinită, inegalitatea 2 dx 2 dx, numită inegalitatea lui Steklov, este valabilă și ne vom asigura că egalitatea în ea este valabilă numai pentru funcțiile de forma f(x) = Un cosx. Cu alte cuvinte, inegalitatea lui Steklov oferă condiții în care micimea derivatei (în pătratul mediu) implică micimea funcției (în pătratul mediu). Soluţie. Să extindem funcția f(x) la intervalul [, ] într-o manieră uniformă. Să notăm funcția extinsă cu același simbol f(x). Apoi funcția extinsă va fi continuă și netedă pe bucăți pe intervalul [, π]. Deoarece funcția f(x) este continuă, atunci f 2 (x) este continuă pe interval și 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Deoarece funcția continuă este pară, atunci b n =, a = prin condiție. În consecință, egalitatea lui Lyapunov ia forma 1 π 2 dx = a 2 π n. (17) Să ne asigurăm că pentru f (x) este îndeplinită concluzia teoremei privind diferențierea termen cu termen a seriei Fourier, adică a =, a n = nb n, b n = na n, n 1. Fie derivata f (x) să sufere îndoituri în punctele x 1, x 2,..., x N în intervalul [, π]. Să notăm x =, x N+1 = π. Să împărțim intervalul de integrare [, π] în N +1 intervale (x, x 1),..., (x N, x N+1), pe fiecare dintre care f(x) este diferențiabil continuu. Apoi, folosind proprietatea de aditivitate a integralei, și apoi integrând pe părți, obținem: b n = 1 π = 1 π = 1 π f (x) sin nxdx = 1 π N f(x) sin nx j= N f (x) sin nx j= x j+1 x j x j+1 x j n n π N j= x j+1 x j x j+1 x j f (x) sin nxdx = f(x) cosnxdx = f(x) cosnxdx = = 1 π [(f(x 1) sin nx 1 f(x) sin nx) + + (f(x 2) sinnx 2 f(x 1) sin nx 1)

54 + (f(x N+1) sin nx N+1 f(x N) sin nx N)] na n = = 1 π na n = = 1 π na n = na n. x j+1 a = 1 f (x)dx = 1 N f (x)dx = π π j= x j = 1 N x j+1 f(x) π = 1 (f(π) f()) = . x j π j= Ultima egalitate apare datorită faptului că funcția f(x) a fost continuată în mod uniform, ceea ce înseamnă f(π) = f(). În mod similar, obținem a n = nb n. Am arătat că teorema privind diferențierea termen cu termen a seriei Fourier pentru o funcție continuă 2π-periodă netedă pe bucăți a cărei derivată în intervalul [, π] suferă discontinuități de primul fel este corectă. Aceasta înseamnă f (x) a 2 + (a n cosnx + b n sin nx) = (na n)sin nx, deoarece a =, a n = nb n =, b n = na n, n = 1, 2,.... Din 2 dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Deoarece fiecare termen din seria din (18) este mai mare sau egal cu termenul corespunzător din seria din (17), atunci 2 dx 2 dx. Reamintind că f(x) este o continuare uniformă a funcției originale, avem 2 dx 2 dx. Ceea ce demonstrează egalitatea lui Steklov. Acum examinăm pentru ce funcții este valabilă egalitatea în inegalitatea lui Steklov. Dacă pentru cel puțin un n 2, coeficientul a n este diferit de zero, atunci a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 PROBLEME 37. Fie funcția netedă pe bucăți f(x) să fie continuă în intervalul [, π]. Demonstrați că atunci când condiția f() = f(π) = este îndeplinită, inegalitatea 2 dx 2 dx, numită și inegalitatea Steklov, este valabilă și asigurați-vă că egalitatea din ea este valabilă numai pentru funcțiile de forma f(x) = B sin x. 38. Fie funcția f continuă în intervalul [, π] și să aibă în ea (cu excepția poate un număr finit de puncte) o derivată f (x) care este pătrat integrabilă. Demonstrați că dacă condițiile f() = f(π) și f(x) dx = sunt îndeplinite, atunci inegalitatea 2 dx 2 dx, numită inegalitatea Wirtinger, este valabilă, iar egalitatea în ea este valabilă numai pentru funcțiile de forma f (x ) = A cosx + B sin x. 56

57 7. Aplicarea seriilor Fourier pentru rezolvarea ecuațiilor cu diferențe parțiale La studierea unui obiect real (fenomen natural, proces de producție, sistem de control etc.), doi factori sunt semnificativi: nivelul cunoștințelor acumulate despre obiectul studiat și gradul de dezvoltarea aparatului matematic. Pe scena modernă cercetarea stiintifica S-a dezvoltat următorul lanț: fenomen model fizic model matematic. Formularea fizică (modelul) problemei este următoarea: se identifică condiţiile de desfăşurare a procesului şi principalii factori care îl influenţează. Formularea (modelul) matematică constă în descrierea factorilor și condițiilor selectate în formularea fizică sub forma unui sistem de ecuații (algebric, diferențial, integral etc.). O problemă se numește bine pusă dacă într-un anumit spațiu funcțional există o soluție a problemei, depinde în mod unic și continuu de condițiile inițiale și la limită. Un model matematic nu este identic cu obiectul luat în considerare, dar este o descriere aproximativă a acestuia. Lăsați capetele șirului să fie fixate și sfoara în sine întinsă. Dacă mutați o sfoară din poziția sa de echilibru (de exemplu, trăgând-o sau lovindu-l), șirul va începe 57

58 ezită. Vom presupune că toate punctele corzii se mișcă perpendicular pe poziția sa de echilibru (vibrații transversale), iar în fiecare moment de timp coarda se află în același plan. Să luăm în acest plan sistemul coordonate dreptunghiulare xou. Atunci, dacă în momentul inițial de timp t = sfoara era situată de-a lungul axei Ox, atunci u va însemna abaterea șirului de la poziția de echilibru, adică poziția punctului șirului cu abscisa x la unui moment arbitrar de timp t corespunde valorii funcției u(x, t). Pentru fiecare valoare fixă ​​a lui t, graficul funcției u(x, t) reprezintă forma corzii care vibrează la momentul t (Fig. 32). La o valoare constantă a lui x, funcția u(x, t) dă legea mișcării unui punct cu abscisă x de-a lungul unei drepte paralele cu axa Ou, derivata u t este viteza acestei mișcări, iar derivata a doua este 2 u t 2 accelerație. Orez. 32. Forțe aplicate unei secțiuni infinitezimale a unui șir Să creăm o ecuație pe care trebuie să o îndeplinească funcția u(x, t). Pentru a face acest lucru, vom face câteva ipoteze mai simplificatoare. Vom considera șirul ca fiind absolut flexibil - 58

59 koy, adică vom presupune că sfoara nu rezistă la îndoire; aceasta înseamnă că tensiunile care apar în șir sunt întotdeauna direcționate tangențial la profilul său instantaneu. Se presupune că sfoara este elastică și supusă legii lui Hooke; aceasta înseamnă că modificarea mărimii forței de tensiune este proporțională cu modificarea lungimii coardei. Să presupunem că șirul este omogen; asta înseamnă că ea densitate liniarăρ este constantă. Neglijăm forțele externe. Aceasta înseamnă că luăm în considerare vibrațiile libere. Vom studia doar mici vibrații ale coardei. Dacă notăm cu ϕ(x, t) unghiul dintre axa absciselor și tangenta la șir în punctul cu abscisa x la momentul t, atunci condiția pentru oscilații mici este ca valoarea ϕ 2 (x, t) poate fi neglijat în comparație cu ϕ (x, t), adică ϕ 2. Deoarece unghiul ϕ este mic, atunci cosϕ 1, ϕ sin ϕ tan ϕ u, prin urmare, valoarea (u x x,) 2 poate fi de asemenea neglijată. Urmează imediat că în timpul procesului de vibrație putem neglija modificarea lungimii oricărei secțiuni a coardei. Într-adevăr, lungimea unei bucăți de sfoară M 1 M 2, proiectată în intervalul axei absciselor, unde x 2 = x 1 + x, este egală cu l = x 2 x () 2 u dx x. x Să arătăm că, în ipotezele noastre, mărimea forței de tensiune T va fi constantă de-a lungul întregului șir. Pentru a face acest lucru, să luăm orice secțiune a șirului M 1 M 2 (Fig. 32) la momentul t și să înlocuim acțiunea secțiunilor aruncate - 59

60 de forțele de întindere T 1 și T 2. Deoarece, conform condiției, toate punctele corzii se deplasează paralel cu axa Ou și nu există forțe exterioare, suma proiecțiilor forțelor de tensiune pe axa Ox trebuie să fi egal cu zero: T 1 cosϕ(x 1, t) + T 2 cosϕ(x 2, t) =. Prin urmare, datorită micii unghiurilor ϕ 1 = ϕ(x 1, t) și ϕ 2 = ϕ(x 2, t), concluzionăm că T 1 = T 2. Să notăm valoarea totală a lui T 1 = T 2 prin T. Acum calculăm suma proiecțiilor F u ale acelorași forțe pe axa Ou: F u = T sin ϕ(x 2, t) T sin ϕ(x 1, t). (2) Deoarece pentru unghiuri mici sin ϕ(x, t) tan ϕ(x, t) și tan ϕ(x, t) u(x, t)/ x, atunci ecuația (2) poate fi rescrisă ca F u T (tg ϕ(x 2, t) tan ϕ(x 1, t)) (u T x (x 2, t) u) x (x 1, t) x x T 2 u x 2(x 1, t) x . Deoarece punctul x 1 este ales arbitrar, atunci F u T 2 u x2(x, t) x. După ce au fost găsite toate forțele care acționează asupra secțiunii M 1 M 2, îi aplicăm a doua lege a lui Newton, conform căreia produsul dintre masă și accelerație este egal cu suma tuturor forțelor care acționează. Masa unei bucăți de sfoară M 1 M 2 este egală cu m = ρ l ρ x, iar accelerația este egală cu 2 u(x, t). Ecuația t 2 a lui Newton ia forma: 2 u t (x, t) x = u 2 α2 2 x2(x, t) x, unde α 2 = T ρ este un număr pozitiv constant. 6

61 Reducând cu x, obținem 2 u t (x, t) = u 2 α2 2 x2(x, t). (21) Ca rezultat, am obținut o ecuație diferențială parțială liniară omogenă de ordinul doi cu coeficienți constanți. Se numește ecuația de vibrație a corzilor sau ecuația de undă unidimensională. Ecuația (21) este în esență o reformulare a legii lui Newton și descrie mișcarea șirului. Dar în formularea fizică a problemei au existat cerințe ca capetele șirului să fie fixe și poziția șirului la un moment dat să fie cunoscută. Vom scrie aceste condiții sub formă de ecuații după cum urmează: a) vom presupune că capetele șirului sunt fixate în punctele x = și x = l, adică vom presupune că pentru tot t relațiile u(, t) =, u (l, t ) =; (22) b) vom presupune că la momentul t = poziția șirului coincide cu graficul funcției f(x), adică vom presupune că pentru tot x [, l] egalitatea u(x,) = f(x); (23) c) vom presupune că în momentul t = punctul șirului cu abscisa x are viteza g(x), adică vom presupune că u (x,) = g(x). (24) t Relațiile (22) se numesc condiții la limită, iar relațiile (23) și (24) se numesc condiții inițiale. Modelul matematic al transversalelor mici libere 61

62 de oscilații ale șirului este că este necesar să se rezolve ecuația (21) cu condițiile la limită (22) și condițiile inițiale (23) și (24) Rezolvarea ecuației micilor oscilații transversale libere ale șirului prin metoda Fourier Soluția de ecuația (21) în regiunea x l,< t . Подставляя (25) в (21), получим: X T = α 2 X T, (26) или T (t) α 2 T(t) = X (x) X(x). (27) Говорят, что произошло разделение переменных. Так как x и t не зависят друг от друга, то левая часть в (27) не зависит от x, а правая от t и общая величина этих отношений 62

63 trebuie să fie o constantă, pe care o notăm cu λ: T (t) α 2 T(t) = X (x) X(x) = λ. De aici obținem două ecuații diferențiale obișnuite: X (x) λx(x) =, (28) T (t) α 2 λt(t) =. (29) În acest caz, condițiile la limită (22) vor lua forma X()T(t) = și X(l)T(t) =. Deoarece ele trebuie să fie satisfăcute pentru tot t, t >, atunci X() = X(l) =. (3) Să găsim soluții pentru ecuația (28) care îndeplinesc condițiile la limită (3). Să luăm în considerare trei cazuri. Cazul 1: λ >. Să notăm λ = β 2. Ecuația (28) ia forma X (x) β 2 X(x) =. Ecuația sa caracteristică k 2 β 2 = are rădăcini k = ±β. Prin urmare, solutie generala ecuația (28) are forma X(x) = C e βx + De βx. Trebuie să selectăm constantele C și D astfel încât să fie îndeplinite condițiile la limită (3), adică X() = C + D =, X(l) = C e βl + De βl =. Deoarece β, acest sistem de ecuații are o soluție unică C = D =. Prin urmare, X(x) și 63

64 u(x, t). Astfel, în cazul 1 am obținut o soluție banală, pe care nu o vom lua în considerare în continuare. Cazul 2: λ =. Atunci ecuația (28) ia forma X (x) = și soluția ei este dată în mod evident de formula: X(x) = C x+d. Substituind această soluție în condițiile la limită (3), obținem X() = D = și X(l) = Cl =, ceea ce înseamnă C = D =. Prin urmare, X(x) și u(x, t) și avem din nou o soluție trivială. Cazul 3: λ