裁きの罪は、当然ながら最も魂を破壊する罪の一つと考えられています...


講義番号60
6.21。 偶数関数と奇数関数のフーリエ級数。
定理:偶数関数の場合、そのフーリエ級数はコサインのみで構成されます。
奇数関数の場合:  .
.
証拠: 偶数関数と奇数関数の定義から、ψ(x) が偶数関数の場合、
 .
.
本当に、

偶数関数の定義により ψ(- x) = ψ(x) であるためです。
同様に、ψ(x) が奇関数である場合、次のように証明できます。
奇数関数 ƒ(x) がフーリエ級数に展開される場合、積 ƒ(x) ·coskx も奇数関数であり、f(x) ·sinkx は偶数関数になります。 したがって、
 (21)
(21)
つまり、奇関数のフーリエ級数には「正弦のみ」が含まれます。
偶数関数がフーリエ級数に展開されると、積 ƒ(x)・sinkx は奇数関数となり、f(x)・coskx は偶数関数となります。
 (22)
(22)
つまり、偶関数のフーリエ級数には「コサインのみ」が含まれます。
結果として得られる公式により、特定の関数が偶数または奇数の場合のフーリエ係数を求める際の計算を簡略化することができ、また次の結果を得ることができます。 区間の一部で定義された関数のフーリエ級数展開 .
多くのタスクでは、関数  間隔で指定されます
間隔で指定されます  。 この関数は、自然数の倍数である角度のサインとコサインの無限和として表す必要があります。 この関数をフーリエ級数に拡張する必要があります。 通常、このような場合、次のように処理が進みます。
。 この関数は、自然数の倍数である角度のサインとコサインの無限和として表す必要があります。 この関数をフーリエ級数に拡張する必要があります。 通常、このような場合、次のように処理が進みます。
与えられた関数をコサインで展開するには、関数  間隔でさらに決定される
間隔でさらに決定される  均等な方法で、つまり だからその合間に
均等な方法で、つまり だからその合間に 
 。 次に、「拡張された」偶数関数の場合、前の段落のすべての引数が有効になり、その結果、係数は次のようになります。 フーリエ級数式によって決定される
。 次に、「拡張された」偶数関数の場合、前の段落のすべての引数が有効になり、その結果、係数は次のようになります。 フーリエ級数式によって決定される
 ,
,
ご覧のとおり、これらの式には関数の値が含まれています。  、間隔でのみ指定されます
、間隔でのみ指定されます  。 機能を拡張するには
。 機能を拡張するには  、間隔で指定
、間隔で指定  、正弦により、この関数を区間内でさらに定義する必要があります。
、正弦により、この関数を区間内でさらに定義する必要があります。  奇妙な方法で、つまり だからその合間に
奇妙な方法で、つまり だからその合間に 
 .
.
次に、フーリエ級数の係数の計算は、次の式を使用して実行する必要があります。
 .
.
定理1.区間で与えられた関数は、無限の方法で次のように拡張できます。 三角級数フーリエ、特に cos または sin において。
コメント。関数  、間隔で指定
、間隔で指定  間隔でさらに定義できます
間隔でさらに定義できます  上記のように行うだけでなく、何らかの方法で。 しかし、関数を任意に再定義すると、フーリエ級数での展開はサインまたはコサインで展開する場合よりも複雑になります。
上記のように行うだけでなく、何らかの方法で。 しかし、関数を任意に再定義すると、フーリエ級数での展開はサインまたはコサインで展開する場合よりも複雑になります。
例。コサインにおけるフーリエ級数の関数を展開する  、間隔で指定
、間隔で指定  (図2a)。
(図2a)。
解決。関数を定義しましょう  合間に
合間に  偶数 (グラフは軸に対して対称です)
偶数 (グラフは軸に対して対称です)  )
)

 ,
,

なぜなら  、 それ
、 それ
で 
 ,
,
で 


6.22 任意の区間で指定された関数のフーリエ級数
これまで、区間で定義された関数を検討してきました。  、この間隔の外側で周期的であるとみなして、ピリオドを付けます。
、この間隔の外側で周期的であるとみなして、ピリオドを付けます。  .
.
では関数を考えてみましょう  、周期は 2 私、つまり
、周期は 2 私、つまり  間隔で
間隔で  , そして、この場合、関数が
, そして、この場合、関数が  フーリエ級数に拡張できます。
フーリエ級数に拡張できます。
入れましょう  、 または
、 または  。 それから着替えるときは
。 それから着替えるときは  から - 私に 私新しい変数
から - 私に 私新しい変数  から異なります
から異なります  に
に  したがって、関数
したがって、関数  からの間隔で指定された関数と考えることができます。
からの間隔で指定された関数と考えることができます。  に
に  この間隔の外側では、ピリオドを使用して定期的に実行されます。
この間隔の外側では、ピリオドを使用して定期的に実行されます。  .
.
それで、  .
.
広がってから  フーリエ級数では、次のようになります。
フーリエ級数では、次のようになります。
 ,
,

 .
.
古い変数に移ります。 信じている 
 、私たちは得ます
、私たちは得ます  ,
, そして
そして  .
.
つまり、関数のフーリエ級数  、間隔で指定
、間隔で指定  、次のようになります:
、次のようになります:
 ,
,
 ,
,

 .
.
関数の場合  が偶数の場合、フーリエ級数の係数を決定する式は簡略化されます。
が偶数の場合、フーリエ級数の係数を決定する式は簡略化されます。
 ,
,
 ,
,

 .
.
機能の場合  奇数:
奇数:
 ,
,
 ,
,

 .
.
関数の場合  間隔で指定
間隔で指定  、その後、インターバル内で継続できます
、その後、インターバル内で継続できます  偶数か奇数かのどちらかです。 区間内で関数が偶数継続の場合
偶数か奇数かのどちらかです。 区間内で関数が偶数継続の場合 
 ,
,

 .
.
区間内の関数の奇数拡張の場合  フーリエ級数の係数は次の式で求められます。
フーリエ級数の係数は次の式で求められます。
 ,
,

 .
.
例。 関数をフーリエ級数に拡張する

複数の円弧の正弦に沿って。
解決。 与えられた関数のグラフを図 3 に示します。 この関数を奇妙な方法で続けてみましょう (図 4)。 正弦波の観点から拡張を実行します。


すべてのオッズ 
 ,
,

代替品を紹介しましょう  。 その後、
。 その後、  私たちは得ます
私たちは得ます  、 で
、 で  我々は持っています
我々は持っています  .
.
したがって
 .
.
6.23. .非周期関数のフーリエ級数展開の概念
メイン領域 (-ℓ, ℓ) で定義された関数は、関数関係 ƒ(x+2 ℓ) = ƒ(x) を使用して、メイン領域を超えて周期的に拡張できます。
非周期関数 ƒ(x) (-∞) の場合 φ(x)= 式 (2.18) は -∞ 軸全体で真になります。< x< ∞ . Можно написать подобное разложение
для функции ƒ(x)= 式 (2.19) は有限区間 (-ℓ, ℓ) でのみ成立します。これは、この区間では ƒ(x) と φ(x) が一致するためです。 したがって、非周期関数は有限区間上のフーリエ級数に拡張できます。 自然界やテクノロジーで発生する多くのプロセスは、一定の間隔で繰り返される傾向があります。 このようなプロセスは周期的と呼ばれ、周期関数によって数学的に記述されます。 このような機能としては、 罪(×)
,
コス(×)
,
罪(wx),
コス(wx)
。 2 つの周期関数の合計 (たとえば、次の形式の関数) ,
一般的に言えば、もはや周期的ではありません。 しかし、次の関係がある場合は証明できます。 w 1
/
w 2
が有理数の場合、この和は周期関数になります。 最も単純な周期プロセスである調和振動は、周期関数によって記述されます。 罪(wx)
そして コス(wx).
より複雑な周期プロセスは、次の形式の有限数または無限数の項で構成される関数によって記述されます。 罪(wx)
そして コス(wx).
次の形式の関数シリーズを考えてみましょう。 このシリーズはと呼ばれます 三角関数; 数字 あ 0
,
b 0
,
ある 1
,
b 1
、A 2
,
b 2
…,
ある n ,
b n ,…
呼ばれます 係数三角関数シリーズ。 シリーズ (1) は、次のように書かれることがよくあります。 三角級数 (2) のメンバーは共通の周期を持っているため、 関数があると仮定しましょう f(×)
はこのシリーズの合計です: この場合、関数は次のように言われます。 f(×)
を三角級数に展開します。 この級数が区間上で一様に収束すると仮定すると、 これらの式によって決定される級数の係数は次のように呼ばれます。 フーリエ係数。 三角級数 (2) は、その係数がフーリエ公式 (4) によって決定されます。 フーリエ付近、機能に対応 f(×).
したがって、周期関数の場合、 f(×)
が収束する三角級数の合計である場合、この級数はそのフーリエ級数になります。 式 (4) は、フーリエ係数が区間上の積分可能なものに対して計算できることを示しています。 関数を思い出してください f(×),
セグメント上で定義される [
ある;
b]
、およびその導関数が有限数の第 1 種の不連続点しか持たない場合、区分的に滑らかであると呼ばれます。 次の定理は、フーリエ級数の関数が分解可能であるための十分な条件を与えます。 ディリクレの定理。
させて 例1. 関数をフーリエ級数に拡張する f(×)=
×、間隔で指定 解決。この関数はディリクレ条件を満たしているため、フーリエ級数で展開できます。 式(4)の利用と部分積分の方法 したがって、関数のフーリエ級数は、 f(×)
見た目がある。 偶数関数と奇数関数のフーリエ級数展開 区間で与えられた関数のサインまたはコサインの級数への展開 任意の周期を持つ関数のフーリエ級数 フーリエ級数の複素表現 一般的な直交関数系におけるフーリエ級数直交系 フーリエ係数の最小特性 ベッセルの不等式 等価性 パーセヴァル 閉じた系 システムの完全性と閉じた状態 偶数関数と奇数関数のフーリエ級数展開 区間 \-1 (I > 0) で定義された関数 f(x) は、偶数関数のグラフが縦軸に関して対称であっても呼び出されます。 線分 J) 上で定義される関数 f(x) (I > 0) は、奇数関数のグラフが原点に対して対称である場合、奇数と呼ばれます。 例。 a) すべての x e について、関数は区間 |-jt, jt) で偶数です。 b) 偶数関数と奇数関数のフーリエ級数展開は、区間で与えられた関数を正弦または正弦の級数に展開するため、関数は奇数です。コサイン 任意の周期を持つ関数のフーリエ級数 フーリエ級数の複素表現 一般直交関数系のフーリエ級数 直交系のフーリエ級数 フーリエ係数の最小性質 ベッセルの不等式 パーセヴァルの等式 閉じた系 システムの完全性と閉じ性 c) 関数 f (x)=x2-x、ただし、定理 1 の条件を満たす関数 f(x) が区間 x| 上で偶数であると仮定するため、 は偶数関数にも奇数関数にも属しません。 それから全員にとって、つまり /(x) cos nx は偶数関数、f(x) sinnx は奇数関数です。 したがって、偶関数 f(x) のフーリエ係数は等しくなります。したがって、偶関数のフーリエ級数は、偶関数 f(x) sin х の形式になります。 したがって、奇関数のフーリエ級数は例 1 の形式になります。関数 4 を区間 -x ^ x ^ n のフーリエ級数に展開します。この関数は偶数であり、定理 1 の条件を満たすため、次のようになります。この場合、そのフーリエ級数は、フーリエ係数を求めるという形式になります。 部分による積分を 2 回適用すると、この関数のフーリエ級数は次のようになります。 または、拡張形式では、この等式は任意の x € に対して有効です。点 x = ±ir では、関数 f(x) = x のグラフと結果の系列の合計が図に示されているため、系列は関数 f(x) = x2 の値と一致します。 コメント。 このフーリエ級数を使用すると、収束する数値級数の 1 つの合計を求めることができます。つまり、x = 0 の場合、例 2 が得られます。関数 /(x) = x を区間上のフーリエ級数に展開します。 6. § 6. 区間上で与えられた関数のサインまたはコサインの系列への拡張 区間上で有界区分的単調関数 / が与えられるとします。 間隔 0| におけるこの関数の値 さまざまな方法でさらに定義できます。 たとえば、セグメント tc] に関数 / を定義すると、/ になります。 この場合、彼らは)「均等な方法でセグメント 0] に拡張される」と言います。 そのフーリエ級数にはコサインのみが含まれます。 関数 /(x) が区間 [-l-, mc] で /( になるように定義されている場合、結果は奇数関数となり、/ は「区間 [-*, 0] まで拡張される」と言います。この場合、フーリエ級数にはサインのみが含まれます。したがって、区間上で定義された各有界単調関数 /(x) は、サインとコサインの両方でフーリエ級数に拡張できます。この関数はフーリエ級数に拡張できます。 a) コサインによって。 b) サインによる。 これにより、幾何学的に、この特性は、図の影付きの領域の場合、次のことを意味します。 10 個の面積は互いに等しい。 特に、周期を持つ関数 f(x) については、偶数関数と奇数関数のフーリエ級数への展開、区間で与えられた関数のサインまたはコサインの級数への展開、任意の関数のフーリエ級数の場合、周期 フーリエ級数の複雑な表記 直交系関数一般のフーリエ級数 直交系のフーリエ級数 フーリエ係数の最小性質 ベッセルの不等式 パーセヴァルの等式 閉じた系 システムの完全性と閉じた系 例 2. 関数 x は周期を持ちます。この関数の奇妙さは、積分を計算しなくても、任意の関数について次のように言えます。証明された特性は、特に、周期 21 の周期関数 f(x) のフーリエ係数が次の式を使用して計算できることを示しています。任意の実数 (関数 cos - と sin の周期は 2/ であることに注意してください)。 例 3. 周期 2 倍の区間で与えられた関数をフーリエ級数に展開します (図 11)。 4 この関数のフーリエ係数を求めてみましょう。 式を入力すると、次のことがわかります。 したがって、フーリエ級数は次のようになります。 点 x = jt (第 1 種不連続点) では、§8 が得られます。 フーリエ級数の複雑な記録 このセクションでは、複雑な解析のいくつかの要素を使用します (複雑な式を使用してここで実行されるすべてのアクションが厳密に正当化されている第 XXX 章を参照してください)。 関数 f(x) がフーリエ級数に展開するための十分な条件を満たすものとします。 次に、線分 x] 上で、次の形式で表すことができます。 オイラーの公式を使用します。 これらの式を cos πx と sin φx の代わりに系列 (1) に置き換えると、次の表記が得られます。 次に、系列 (2) は次のようになります。したがって、フーリエ級数 (1) は複素数形式 (3) で表されます。 積分を通して係数の式を求めてみましょう。 同様に、 с 、 с_п 、 с の最終的な式は次のように書けることがわかります。 。 係数 は関数の複素フーリエ係数と呼ばれます。周期を持つ周期関数の場合、フーリエ級数の複素形式は次の式を使用して計算されます。級数の収束。 ) と (4) は次のように理解されます: 級数 (3) と (4) は収束と呼ばれます。 与えられた値 g、制限がある場合 例。 周期関数を複素フーリエ級数に展開する この関数は、フーリエ級数に展開するための十分な条件を満たします。 この関数の複素フーリエ係数を求めてみましょう。 偶数 n に対して奇数、つまり、要するに。 値を代入して)、最終的にこの級数は次のように書くこともできることに注意してください: 一般直交関数系のフーリエ級数 9.1. 直交関数系 区間 [a, 6] で定義され積分可能なすべての (実) 関数の集合を平方で表します。つまり、積分が存在するすべての関数 f(x) が連続です。区間 [a , 6] では 6] に属し、そのルベーグ積分の値はリーマン積分の値と一致します。 意味。 関数系は、特に条件 (1) がまったく同じゼロではないことを仮定している場合、区間 [a, b\ 上で直交] と呼ばれます。 積分はルベーグの意味で理解されます。 直交系のフーリエ級数 区間 (a, 6) に関数の直交系があり、級数 (cj = const) がこの区間で関数 f(x) に収束するとします。最後の等式の両辺を乗算します。 by -fixed) と a から 6 までの x を積分すると、システムの直交性により、この演算は一般的に純粋に形式的な性質を持つことがわかります。 ただし、場合によっては、たとえば、級数 (4) が一様に収束し、すべての関数が連続で、区間 (a, 6) が有限である場合、この操作は正当です。 しかし、今の私たちにとって重要なのは、正式な解釈です。 そこで、関数を与えてみましょう。 式 (5) を使って数値 c* を作成して書きます。この系 (^n(i)) に対する関数 f(x) の級数を、数値 Cn と呼びます。は、このシステムに関する関数 f(x) のフーリエ係数と呼ばれます。 式 (6) の ~ 記号は、数値 Cn が式 (5) によって関数 f(x) に関連付けられることを意味するだけです (右辺の級数がまったく収束することは想定されておらず、ましてや関数 f に収束することも想定されていません) (x))。 したがって、このシリーズの特性は何でしょうか?という疑問が当然生じます。 それはどのような意味で関数 f(x) を「表す」のでしょうか? 9.3. 平均収束の定義。 ノルムが定理 6 の空間内にある場合、数列は平均して要素 ] に収束します。数列 ) が一様に収束する場合、平均して収束します。 したがって、積分 (*) は ak = sk で最小値をとります。この積分は、関数 /(x) を Tn(x) の線形結合によって二乗平均近似したものと呼ばれます。 したがって、関数 /\ の二乗平均平方根近似は、次の場合に最小値を取ります。 Tn(x) が関数 /(x) のシステム (.ak = sk と設定すると、(7) から式 (9) のフーリエ級数の 71 番目の部分和であるとき、式 (9) はベッセル恒等式と呼ばれます。辺が負でない場合、そこからベッセルの不等式が続きます。私はここで任意に説明しているので、ベッセルの不等式は強化された形式で表すことができます。つまり、任意の関数について、正規直交系におけるこの関数の一連の二乗フーリエ係数が収束します。 。 この系は区間 [-x, m] で正規直交であるため、不等式 (10) を三角フーリエ級数の通常の表記に変換すると、可積分平方を持つ任意の関数 /(x) に対して有効な関係 do が得られます。 f2(x) が可積分であれば、不等式 (11) の左側の級数が収束するための必要条件により、それが得られます。 Parseval の等式 一部のシステム (^ (x)) では、式 (10) の不等号を (すべての関数 f(x) 6 × に対して) 等号に置き換えることができます。 結果として得られる等式は、パーセヴァル・ステクロフ等式 (完全性条件) と呼ばれます。 ベッセルの恒等式 (9) により、条件 (12) を等価な形式で書くことができます。したがって、完全性条件が満たされるということは、関数 /(x) のフーリエ級数の部分和 Sn(x) が関数に収束することを意味します。 /(x) 平均、つまり 空間のノルムに従って 6]。 意味。 正規直交系 (すべての関数が c の形式の線形結合によって任意の精度で平均して十分に近似できる場合、b2[ау b] で完全であると呼ばれます) 多数のつまり、任意の関数 /(x) € b2[a, b\ および任意の e > 0 に対して、自然数 nq と数値 a\, a2y... が存在する場合、No 上記の推論から、定理に従います。 7. 直交正規化によってシステム ) が空間内で完全である場合、このシステムの任意の関数 / のフーリエ級数は平均で、つまりノルムに従って f(x) に収束します。三角関数システムは で完全であることがわかります。スペース。これはステートメントを意味します。 定理 8. 関数が /o の場合、その三角関数フーリエ級数は平均してそれに収束します。 9.5。 閉鎖系。 システムの完全性と閉鎖性 定義。 正規直交系の関数 \ は、空間 Li\a, b) にすべての関数に直交する非ゼロ関数が存在しない場合、正規直交系の完全性と閉鎖性の概念が一致します。 演習 1. 関数 2 を区間 (-i-, x) のフーリエ級数に展開します。 2. 関数を区間 (-tr, tr) のフーリエ級数に展開します。 3. 関数 4 を区間 (-tr, tr) のフーリエ級数に展開します。区間 (-tr, tr) を区間 (-jt, tr) 関数のフーリエ級数に展開します。 5. 関数 f(x) = x + x を区間 (-jt, tr) のフーリエ級数に展開します。 6. 関数 n を区間 (-jt, tr) のフーリエ級数に展開します。 7. 関数 /(x) = sin2 x を区間 (-tr, x) のフーリエ級数に展開します。 8. 関数 f(x) = y を区間 (-tr, jt) のフーリエ級数に展開します。 9. 関数 f(x) = | を展開します。 罪x|。 10. 関数 f(x) = § を区間 (-π-, π) のフーリエ級数に展開します。 11. 関数 f(x) = sin § を区間 (-tr, tr) のフーリエ級数に展開します。 12. 区間 (0, x) で与えられる関数 f(x) = n -2x をフーリエ級数に拡張し、区間 (-x, 0) に拡張します。 a) 均等な方法で。 b) 奇妙な方法で。 13. 区間 (0, x) で指定された関数 /(x) = x2 を正弦のフーリエ級数に展開します。 14. 区間 (-2,2) で与えられた関数 /(x) = 3 をフーリエ級数に展開します。 15. 区間 (-1,1) で与えられた関数 f(x) = |x| をフーリエ級数に展開します。 16. 区間 (0,1) で指定された関数 f(x) = 2x を正弦のフーリエ級数に展開します。 周期 2π の周期関数のフーリエ級数。
フーリエ級数を使用すると、周期関数を成分に分解して調べることができます。 交流電流と電圧、クランク機構の変位、速度と加速度、音波は、工学計算における周期関数の使用の典型的な実際的な例です。 フーリエ級数展開は、すべてが 実用的な重要性区間 -π ≤x≤ π の関数は、収束三角級数の形式で表すことができます (級数は、その項で構成される部分和のシーケンスが収束する場合に収束していると見なされます)。 sinx と cosx の合計による標準 (= 通常の) 表記法 f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...、 ここで、a 0、a 1、a 2、...、b 1、b 2、... は実定数です。 ここで、-π から π までの範囲について、フーリエ級数係数は次の式を使用して計算されます。 係数 a o 、 a n 、 b n は次のように呼ばれます。 フーリエ係数、それらが見つかると、シリーズ (1) が呼び出されます。 フーリエの隣には、関数 f(x) に対応します。 級数 (1) の場合、項 (a 1 cosx+b 1 sinx) は最初のまたはと呼ばれます。 基本高調波、 シリーズを記述するもう 1 つの方法は、関係 acosx+bsinx=csin(x+α) を使用することです。 f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n) ここで、a o は定数であり、1 =(a 1 2 +b 1 2) 1/2、n =(a n 2 +b n 2) 1/2 - さまざまな成分の振幅であり、a n =arctg と等しくなります。 a n /b n。 級数 (1) の場合、項 (a 1 cosx+b 1 sinx) または c 1 sin(x+α 1) は最初のまたはと呼ばれます。 基本高調波、(a 2 cos2x+b 2 sin2x) または c 2 sin(2x+α 2) と呼ばれます 第二高調波等々。 複素信号を正確に表現するには、通常、無限の数の項が必要です。 ただし、多くの実際的な問題では、最初の数項だけを考慮するだけで十分です。 周期 2π の非周期関数のフーリエ級数。
非周期関数の拡張。 関数 f(x) が非周期的である場合、それは x のすべての値についてフーリエ級数に展開できないことを意味します。 ただし、幅 2π の任意の範囲にわたる関数を表すフーリエ級数を定義することは可能です。 非周期関数が与えられた場合、特定の範囲内で f(x) の値を選択し、その範囲外で 2π 間隔でそれらを繰り返すことによって、新しい関数を構築できます。 なぜなら 新機能は 2π の周期で周期的であるため、x のすべての値についてフーリエ級数に展開できます。 たとえば、関数 f(x)=x は周期的ではありません。 ただし、0 から 2π までの区間でフーリエ級数に展開する必要がある場合は、この区間の外側で周期 2π の周期関数が構築されます (下図を参照)。 f(x)=x などの非周期関数の場合、フーリエ級数の合計は、指定された範囲内のすべての点で f(x) の値と等しくなりますが、点については f(x) と等しくありません。範囲外です。 2π 範囲の非周期関数のフーリエ級数を求めるには、同じフーリエ係数の式が使用されます。 偶数関数と奇数関数。
彼らは関数 y=f(x) と言います。 平、x のすべての値に対して f(-x)=f(x) の場合。 偶数関数のグラフは常に y 軸に関して対称です (つまり、鏡像です)。 偶数関数の 2 つの例: y=x2 と y=cosx。 彼らは関数 y=f(x) と言います。 奇数、 x のすべての値に対して f(-x)=-f(x) の場合。 奇数関数のグラフは常に原点に対して対称です。 多くの関数は偶数でも奇数でもありません。 コサインでのフーリエ級数展開。
周期 2π の偶数周期関数 f(x) のフーリエ級数にはコサイン項のみが含まれ (つまり、サイン項は含まれません)、次のものが含まれる場合があります。 永久会員。 したがって、 ここで、フーリエ級数の係数は次のとおりです。
周期 2π の奇数周期関数 f(x) のフーリエ級数には、サインを含む項のみが含まれます (つまり、コサインを含む項は含まれません)。 したがって、 ここで、フーリエ級数の係数は次のとおりです。 半周期のフーリエ級数。
関数が 0 から 2π だけでなく、0 から π までの範囲に対して定義されている場合、その関数はサインのみまたはコサインのみで系列に展開できます。 結果として得られるフーリエ級数は次のように呼ばれます。 半周期でフーリエに近くなります。 分解を取得したい場合 コサインによる半周期フーリエ 0 から π までの範囲の関数 f(x) を作成するには、偶数周期関数を構築する必要があります。 図では、 以下は、x=0 から x=π までの区間に基づいて構築された関数 f(x)=x です。 偶数関数は f(x) 軸に対して対称なので、図に示すように線 AB を引きます。 下に。 考慮した間隔の外側で、結果として得られる三角形の形状が 2π の周期で周期的であると仮定すると、最終的なグラフは次のようになります。 図の 下に。 前と同様にコサインでフーリエ展開を取得する必要があるため、フーリエ係数 a o と a n を計算します。 入手する必要がある場合は、 フーリエ半周期正弦展開 0 から π までの範囲の関数 f(x) を作成するには、奇数の周期関数を作成する必要があります。 図では、 以下は、x=0 から x=π までの区間に基づいて構築された関数 f(x)=x です。 奇数関数は原点に対して対称であるため、図に示すように直線 CD を作成します。 考慮した間隔の外側で、結果の鋸歯状信号が 2π の周期で周期的であると仮定すると、最終的なグラフは図に示す形式になります。 前と同様に、正弦に関して半サイクルのフーリエ展開を取得する必要があるため、フーリエ係数を計算します。 b 任意の区間のフーリエ級数。
周期 L による周期関数の展開。 周期関数 f(x) は、x が L ずつ増加するにつれて繰り返されます。 f(x+L)=f(x)。 以前に検討した周期 2π の関数から周期 L の関数への遷移は、変数の変更を使用して実行できるため、非常に簡単です。 -L/2≤x≤L/2 の範囲で関数 f(x) のフーリエ級数を求めるには、関数 f(x) が u に対して 2π の周期を持つように新しい変数 u を導入します。 u=2πx/L の場合、u=-π の場合は x=-L/2、u=π の場合は x=L/2 となります。 また、f(x)=f(Lu/2π)=F(u) とします。 フーリエ級数 F(u) の形式は次のとおりです。 (積分の極限は、長さ L の任意の区間 (たとえば、0 から L まで) に置き換えることができます。 区間 L≠2π で指定された関数の半サイクルのフーリエ級数。
代入 u=πх/L の場合、x=0 から x=L までの区間は u=0 から u=π までの区間に対応します。 したがって、関数はコサインのみまたはサインのみの級数に展開できます。 V 半周期のフーリエ級数. 0 から L までの範囲のコサイン展開は次の形式になります。 フーリエ級数は、特定の周期を持つ任意の関数を級数の形式で表現したものです。 で 全体像 この決断は直交基底での要素の分解と呼ばれます。 関数のフーリエ級数への拡張は、積分、微分、および引数と畳み込みによる式のシフト中のこの変換の特性により、さまざまな問題を解決するための非常に強力なツールです。 馴染みのない人 高等数学、フランスの科学者フーリエの作品と同様に、これらの「シリーズ」が何であるか、そしてそれらが何に必要であるかを理解できない可能性がほとんどです。 一方、この変化は私たちの生活に完全に組み込まれています。 数学者だけでなく、物理学者、化学者、医師、天文学者、地震学者、海洋学者など多くの人によって使用されています。 時代を先取りした発見をした偉大なフランスの科学者の業績も詳しく見てみましょう。 フーリエ級数は (分析などと同様に) 手法の 1 つであり、人が音を聞くたびにこのプロセスが発生します。 私たちの耳は、弾性媒体内の素粒子を、異なる高さのトーンの連続する音量レベルの列 (スペクトルに沿った) に自動的に変換します。 次に、脳はこのデータを私たちに馴染みのある音に変換します。 これらすべては私たちの欲望や意識の外で自然に起こりますが、これらのプロセスを理解するには、高等数学を学ぶには数年かかります。 フーリエ変換は、解析的、数値的、その他の方法を使用して実行できます。 フーリエ級数とは、海の潮汐や光波から太陽 (およびその他の天体) の活動のサイクルに至るまで、あらゆる振動プロセスを分解する数値的手法を指します。 これらの数学的手法を使用すると、関数を分析して、最小値から最大値へ、そしてその逆に移動する一連の正弦波成分として振動プロセスを表すことができます。 フーリエ変換は、特定の周波数に対応する正弦波の位相と振幅を記述する関数です。 このプロセスは、次のような非常に複雑な方程式を解くために使用できます。 動的プロセス、熱、光、または電気エネルギーの影響下で発生します。 また、フーリエ級数を使用すると、複雑な振動信号の定数成分を分離できるため、医学、化学、天文学で得られる実験観測を正確に解釈できるようになります。 この理論の創始者はフランスの数学者ジャン・バティスト・ジョセフ・フーリエです。 この変化は後に彼の名前にちなんで名付けられました。 当初、科学者は彼の方法を使用して、熱伝導率のメカニズム、つまり体内での熱の広がりを研究し、説明しました。 固体。 フーリエは、初期の不規則分布を単純な正弦波に分解でき、それぞれが独自の温度の最小値と最大値、および位相を持つことを示唆しました。 この場合、そのような各コンポーネントは最小値から最大値まで測定され、その逆も測定されます。 曲線の上部と下部のピーク、および各高調波の位相を記述する数学関数は、温度分布式のフーリエ変換と呼ばれます。 理論の著者がまとめた 一般的な機能数学的に説明するのは難しい分布を、非常に便利な一連のコサインとサインに変換し、これらを合わせると元の分布が得られます。 科学者の同時代人、つまり 19 世紀初頭の主要な数学者たちは、この理論を受け入れませんでした。 主な反対意見は、直線または不連続曲線を記述する不連続関数は連続的な正弦波式の合計として表現できるというフーリエの主張でした。 例として、ヘヴィサイド ステップを考えてみましょう。その値は、不連続部の左側では 0、右側では 1 です。 この関数は、回路が閉じているときの一時変数に対する電流の依存性を記述します。 当時の理論の同時代人は、不連続な式が指数関数、正弦関数、線形関数、二次関数などの連続した通常の関数の組み合わせによって記述される同様の状況に遭遇したことがありませんでした。 結局のところ、数学者の発言が正しければ、無限の三角関数フーリエ級数を合計することによって、類似したステップが多数ある場合でも、ステップ式の正確な表現を得ることができます。 19 世紀初頭、そのような発言はばかげているように思えました。 しかし、あらゆる疑問にもかかわらず、多くの数学者はこの現象の研究範囲を拡大し、熱伝導率の研究を超えました。 しかし、ほとんどの科学者は「正弦波系列の合計は不連続関数の正確な値に収束することができるのか?」という疑問に悩まされ続けました。 収束の問題は、無限の数列を合計する必要がある場合に必ず発生します。 この現象を理解するために、古典的な例を考えてみましょう。 後続の各ステップが前のステップの半分の大きさであれば、壁に到達できるでしょうか? ターゲットまで 2 メートルの地点にいて、最初の一歩で中間点まで進み、次の一歩で 4 分の 3 マークまで進み、5 歩目でほぼ 97 パーセントをカバーしたことになるとします。 ただし、どれだけ多くのステップを踏んでも、厳密な数学的な意味で意図した目標を達成することはできません。 数値計算を使用すると、最終的には指定された距離まで近づけることが可能であることが証明できます。 この証明は、2 分の 1、4 分の 1 などの合計が 1 になる傾向があることを証明するのと同じです。 この問題は 19 世紀末、潮の強さを予測するためにフーリエ級数を使用しようとしたときに再び提起されました。 このとき、ケルビン卿は、軍や商船の船員がこれを追跡できるアナログ コンピューティング デバイスである機器を発明しました。 自然現象。 このメカニズムは、年間を通して特定の港で注意深く測定された潮の高さと対応する時点の表から位相と振幅のセットを決定しました。 各パラメータは潮位高さ表現の正弦波成分であり、正規成分の 1 つでした。 測定値はケルビン卿の計算装置に入力され、翌年の水位の高さを時間の関数として予測する曲線が合成されました。 すぐに、世界中のすべての港に対して同様の曲線が作成されました。 当時は、多数の計数要素を備えた津波予測器が多数の位相と振幅を計算できるため、より正確な予測を提供できることは明らかであると思われました。 しかし、合成すべき潮汐表現に急激なジャンプが含まれる場合、つまり不連続な場合には、このパターンは観察されないことが判明した。 時刻表のデータがデバイスに入力されると、いくつかのフーリエ係数が計算されます。 正弦波成分のおかげで、元の関数が復元されます (見つかった係数に従って)。 元の式と再構築された式の間の相違は、任意の時点で測定できます。 計算と比較を繰り返し実行しても、最大誤差の値が減少しないことは明らかです。 ただし、それらは不連続点に対応する領域に局在しており、他の点ではゼロになる傾向があります。 1899 年に、この結果はエール大学のジョシュア ウィラード ギブスによって理論的に確認されました。 フーリエ解析は、特定の間隔にわたる無限数のスパイクを含む式には適用できません。 一般に、フーリエ級数は、元の関数が実数の結果で表される場合、 物理的次元、常に収束します。 関数の特定のクラスに対するこのプロセスの収束に関する疑問は、数学における新しい分野、たとえば一般化された関数の理論の出現につながりました。 彼女には、L. シュワルツ、J. ミクシンスキー、J. テンプルなどの名前が関連付けられています。 この理論の枠組みの中で、ディラック デルタ関数 (点の微小な近傍に集中する単一領域の領域を表す) やヘビサイドの「ステップ」などの式に対する明確で正確な理論的基礎が作成されました。 この研究のおかげで、フーリエ級数は、点電荷、点質量、磁気双極子、ビームへの集中荷重などの直観的な概念を含む方程式や問題の解決に適用できるようになりました。 フーリエ級数は、干渉の原理に従って、複雑な形式をより単純なものに分解することから始まります。 たとえば、熱流の変化は、不規則な形の断熱材でできたさまざまな障害物を通過することや、地震や軌道の変化といった地表の変化によって説明されます。 天体- 惑星の影響。 原則として、単純な古典系を記述するこのような方程式は、個々の波ごとに簡単に解くことができます。 フーリエは、単純な解を合計して、より複雑な問題の解を生み出すこともできることを示しました。 数学用語では、フーリエ級数は式を高調波 (コサインとサイン) の和として表す手法です。 したがって、この分析は「調和分析」とも呼ばれます。 コンピューター技術が誕生する前、フーリエ技術は 最高の武器私たちの世界の波の性質を扱う科学者の武器庫にあります。 複雑な形式のフーリエ級数を使用すると、ニュートン力学の法則を直接適用できる単純な問題だけでなく、 基本方程式。 19 世紀におけるニュートン科学の発見のほとんどは、フーリエの技術によってのみ可能になりました。 コンピュータの発展により、フーリエ変換は定性的なレベルにまで上昇しました 新しいレベル。 この手法は、科学技術のほぼすべての分野でしっかりと確立されています。 例としては、デジタル オーディオとビデオがあります。 その実装は、19 世紀初頭にフランスの数学者によって開発された理論のおかげでのみ可能になりました。 したがって、複素形式のフーリエ級数により、研究に画期的な進歩をもたらすことができました。 宇宙空間。 さらに、半導体材料とプラズマの物理学、マイクロ波音響学、海洋学、レーダー、地震学の研究にも影響を与えました。 数学では、フーリエ級数は、任意の複雑な関数をより単純な関数の合計として表す方法です。 一般に、そのような式の数は無限になる可能性があります。 さらに、計算でそれらの数がより多く考慮されるほど、最終結果はより正確になります。 原生動物として最もよく使用される 三角関数コサインまたはサイン。 この場合のフーリエ級数を三角関数といい、その式の解を調和展開といいます。 この方法は数学において重要な役割を果たします。 まず第一に、三角関数は関数を描写し、研究するための手段を提供します。これは理論の主要な装置です。 さらに、数理物理学の多くの問題を解決することもできます。 最後に、この理論は、数学科学の多くの非常に重要な分野 (積分理論、周期関数理論) の発展に貢献しました。 さらに、これは以下の実変数関数の開発の出発点となり、調和解析の基礎も築きました。 (2.18)
(2.18) (2.19)
(2.19)3.2. 三角関数シリーズ。 フーリエ係数
 .
(2)
.
(2) 、級数の合計が収束すると、周期を持つ周期関数でもあります。
、級数の合計が収束すると、周期を持つ周期関数でもあります。  .
. .
(3)
.
(3) 、次の式を使用して係数を決定できます。
、次の式を使用して係数を決定できます。 ,
,  ,
, .
(4)
.
(4)3.3. フーリエ級数の収束

 -周期関数、つまり このような関数では、いつでもフーリエ級数を構築できます。 しかし、この級数は次の関数に収束するでしょうか? f(×)
そしてどのような条件下で?
-周期関数、つまり このような関数では、いつでもフーリエ級数を構築できます。 しかし、この級数は次の関数に収束するでしょうか? f(×)
そしてどのような条件下で? -周期関数 f(×)
区分的に滑らかです
-周期関数 f(×)
区分的に滑らかです  。 次に、そのフーリエ級数は次のように収束します。 f(×)
連続性の各点と値に応じて 0,5(f(×+0)+
f(×-0))
限界点で。
。 次に、そのフーリエ級数は次のように収束します。 f(×)
連続性の各点と値に応じて 0,5(f(×+0)+
f(×-0))
限界点で。 .
. 、フーリエ係数を求めます。
、フーリエ係数を求めます。



























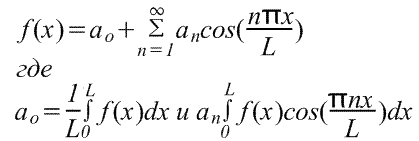
人間とフーリエ変換

フーリエ変換についてさらに詳しく

歴史的背景
変革の原理と同時代人の視点

フーリエ理論についてフランスの数学者を混乱させたのは何ですか?
フーリエ級数の収束: 例

収束の問題: 再臨、またはケルビン卿の道具
不連続な機能によってプロセスが中断されたらどうなるでしょうか?

フーリエ級数の収束と数学一般の発展
フーリエ法
フーリエ級数 - 「コンピュータ時代」以前の理想的な手法

今日のフーリエ級数
三角フーリエ級数