Veliko ljudi se želi naučiti kazaškega jezika, a ne vedo, kje začeti. Stroški ...
Predavanje št. 60
6.21. Fourierjeva vrsta za sode in lihe funkcije.
Izrek: Za katero koli sodo funkcijo je njen Fourierjev niz sestavljen samo iz kosinusov.
Za katero koli čudno funkcijo: 
.
Dokaz: Iz definicije sode in lihe funkcije sledi, da če je ψ(x) soda funkcija, potem
.
res,
saj je po definiciji sode funkcije ψ(- x) = ψ(x).
Podobno lahko dokažemo, da če je ψ(x) liha funkcija, potem
Če liho funkcijo ƒ(x) razširimo v Fourierjev niz, potem je tudi produkt ƒ(x) ·coskx liha funkcija, ƒ(x) ·sinkx pa soda funkcija; torej,
(21)
tj. Fourierjeva vrsta lihe funkcije vsebuje »samo sinuse«.
Če sodo funkcijo razširimo v Fourierjev niz, potem je produkt ƒ(x)·sinkx liha funkcija in ƒ(x)·coskx soda funkcija, potem:
(22)
to pomeni, da Fourierjeva vrsta sode funkcije vsebuje »samo kosinuse«.
Dobljene formule omogočajo poenostavitev izračunov pri iskanju Fourierjevih koeficientov v primerih, ko je dana funkcija soda ali liha, in tudi pridobitev Razširitev v Fourierjev niz funkcije, definirane na delu intervala .
Pri številnih nalogah funkcija 
je določen v intervalu 
. To funkcijo je treba predstaviti kot neskončno vsoto sinusov in kosinusov kotov, ki so večkratniki naravnih števil, tj. potrebno je funkcijo razširiti v Fourierjev niz. Običajno v takih primerih potekajo na naslednji način.
Če želite razširiti dano funkcijo v kosinuse, funkcijo 
dodatno določena v intervalu 
na enakomeren način, tj. tako da v intervalu 
. Potem so za "razširjeno" sodo funkcijo veljavni vsi argumenti v prejšnjem odstavku in posledično koeficienti Fourierjeve vrste določeno s formulami
,
Te formule, kot vidimo, vključujejo vrednosti funkcije 
, določen samo v intervalu 
. Za razširitev funkcije 
, določen v intervalu 
, s sinusi, je potrebno to funkcijo dodatno definirati v intervalu 
na čuden način, tj. tako da v intervalu 
.
Nato je treba izračunati koeficiente Fourierjeve serije z uporabo formul
.
1. izrek. Funkcijo, podano na intervalu, je mogoče razširiti na neskončno veliko načinov v trigonometrično Fourierjevo vrsto, zlasti v cos ali sin.
Komentiraj. funkcija 
, določen v intervalu 
lahko dodatno opredelimo v intervalu 
na kakršen koli način in ne samo kot je bilo storjeno zgoraj. Toda s poljubno redefinicijo funkcije bo razširitev v Fourierjev niz bolj zapletena kot tista, ki jo dobimo pri razširitvi v sinuse ali kosinuse.
Primer. Razširi funkcijo v Fourierjev niz v kosinusih 
, določen v intervalu 
(slika 2a).
rešitev. Definirajmo funkcijo 
v intervalu 
sodo (graf je simetričen glede na os 
)
,
Ker 
, To
pri 
,
pri 
6.22. Fourierjeva vrsta za funkcijo, podano na poljubnem intervalu
Do sedaj smo obravnavali funkcijo, definirano v intervalu 
, pri čemer velja, da je periodično zunaj tega intervala, z obdobjem 
.
Oglejmo si zdaj funkcijo 
, katerega obdobje je 2 l, tj. 
na intervalu 
, in pokažite, da je v tem primeru funkcija 
lahko razširimo v Fourierjev niz.
Postavimo 
, oz 
. Potem pri menjavi 
od – l prej l nova spremenljivka 
razlikuje od 
prej 
in s tem funkcijo 
lahko obravnavamo kot funkcijo, določeno v intervalu od 
prej 
in periodično zunaj tega intervala, s periodo 
.
Torej, 
.
Ko se je razširil 
v Fourierjevem nizu dobimo
,
.
Če preidemo na stare spremenljivke, tj. verjeti 
, dobimo 
,
in 
.
To je Fourierjeva vrsta za funkcijo 
, določen v intervalu 
, bo videti takole:
,
,
.
Če funkcija 
je sodo, potem so formule za določanje koeficientov Fourierjevega niza poenostavljene:
,
,
.
V primeru funkcije 
Čuden:
,
,
.
Če funkcija 
določeno v intervalu 
, potem se lahko nadaljuje v intervalu 
sodo ali liho. V primeru enakomernega nadaljevanja funkcije v intervalu 
,
.
V primeru lihe razširitve funkcije v intervalu 
koeficiente Fourierove vrste najdemo s formulami
,
.
Primer. Razširite funkcijo v Fourierjev niz
vzdolž sinusov večih lokov.
rešitev. Graf dane funkcije je predstavljen na sliki 3. Nadaljujmo funkcijo na čuden način (slika 4), tj. Širitev bomo izvedli po sinusih.
Vse možnosti 
,
Predstavimo zamenjavo 
. Nato pri 
dobimo 
, pri 
imamo 
.
torej
.
6.23. .Koncept raztezanja neperiodičnih funkcij v Fourierove vrste
Funkcijo, definirano v glavnem območju (-ℓ, ℓ), je mogoče periodično razširiti izven glavnega območja z uporabo funkcionalne relacije ƒ(x+2 ℓ) = ƒ(x).
Za neperiodično funkcijo ƒ(x) (-∞ φ(x)= Formula (2.18) bo veljala na celotni -∞ osi< x< ∞ . Можно написать подобное разложение
для функции ƒ(x)= Formula (2.19) bo resnična le na končnem intervalu (-ℓ, ℓ), saj na tem intervalu ƒ(x) in φ(x) sovpadata. Tako lahko neperiodično funkcijo razširimo v Fourierjev niz na končnem intervalu. Številni procesi, ki se dogajajo v naravi in tehnologiji, se v določenih intervalih ponavljajo. Takšni procesi se imenujejo periodični in so matematično opisani s periodičnimi funkcijami. Takšne funkcije vključujejo greh(x)
,
cos(x)
,
greh(wx),
cos(wx)
. Vsota dveh periodične funkcije, na primer funkcija oblike ,
na splošno ni več periodičen. Lahko pa se dokaže, da če razmerje w 1
/
w 2
je racionalno število, potem je ta vsota periodična funkcija. Najenostavnejše periodične procese – harmonična nihanja – opisujejo periodične funkcije greh(wx)
in cos(wx).
Bolj zapletene periodične procese opisujejo funkcije, sestavljene bodisi iz končnega ali neskončnega števila členov oblike greh(wx)
in cos(wx).
Oglejmo si funkcionalno serijo oblike: Ta serija se imenuje trigonometrična; številke A 0
,
b 0
,
a 1
,
b 1
,A 2
,
b 2
…,
a n ,
b n ,…
se imenujejo koeficientov trigonometrične vrste. Serija (1) je pogosto zapisana na naslednji način: Ker imajo členi trigonometrične vrste (2) skupno periodo Predpostavimo, da funkcija f(x)
je vsota te serije: V tem primeru pravijo, da funkcija f(x)
se razširi v trigonometrično vrsto. Ob predpostavki, da ta niz enakomerno konvergira na intervalu Koeficienti nizov, določenih s temi formulami, se imenujejo Fourierjevi koeficienti. Trigonometrične vrste (2), katerih koeficienti so določeni s Fourierjevimi formulami (4), se imenujejo blizu Fourierja, ki ustreza funkciji f(x).
Torej, če je periodična funkcija f(x)
je vsota konvergentne trigonometrične vrste, potem je ta vrsta njena Fourierjeva vrsta. Formule (4) kažejo, da je mogoče Fourierjeve koeficiente izračunati za katero koli integrabilo na intervalu Spomnimo se, da funkcija f(x),
definirana na segmentu [
a;
b]
, imenujemo delno gladko, če imata in njen derivat največ končno število diskontinuitetnih točk prve vrste. Naslednji izrek daje zadostne pogoje za razgradljivost funkcije v Fourierjev niz. Dirichletov izrek.
Pustiti Primer 1. Razširite funkcijo v Fourierjev niz f(x)=
x, določeno na intervalu rešitev. Ta funkcija izpolnjuje Dirichletove pogoje in jo je zato mogoče razširiti v Fourierjev niz. Uporaba formul (4) in metode integracije po delih Torej Fourierjeva vrsta za funkcijo f(x)
ima pogled. Razširitev v Fourierjev niz sodih in lihih funkcij Razširitev funkcije, podane na intervalu, v vrsto v sinusih ali kosinusih Fourierjeva vrsta za funkcijo s poljubno periodo Kompleksna predstavitev Fourierjeve vrste Fourierjeva vrsta v splošnih ortogonalnih sistemih funkcij Fourierjeva vrsta v ortogonalni sistem Minimalna lastnost Fourierjevih koeficientov Besselova neenakost Enakost Parseval Zaprti sistemi Popolnost in zaprtost sistemov Razširitev sode in lihe funkcije v Fourierjev niz Funkcijo f(x), definirano na intervalu \-1, kjer je I > 0, kličemo sodo, če je graf sode funkcije simetričen glede na ordinatno os. Funkcija f(x), definirana na segmentu J), kjer je I > 0, se imenuje liha, če je graf lihe funkcije simetričen glede na izhodišče. Primer. a) Funkcija je soda na intervalu |-jt, jt), saj je za vse x e b) Funkcija je liha, saj je Fourierjeva razširitev sode in lihe funkcije v vrsto razteg funkcije, podane na intervalu, v vrsto po sinusih oz. kosinusov Fourierjeva vrsta za funkcijo s poljubno periodo Kompleksna predstavitev Fourierjeve vrste Fourierjeva vrsta za splošne ortogonalne sisteme funkcij Fourierjeva vrsta za ortogonalni sistem Minimalna lastnost Fourierjevih koeficientov Besselova neenakost Parsevalova enakost Zaprti sistemi Popolnost in zaprtost sistemov c) Funkcija f (x)=x2-x, kjer ne pripada niti sodim niti lihim funkcijam, saj Naj bo funkcija f(x), ki izpolnjuje pogoje iz izreka 1, soda na intervalu x|. Potem za vse, tj. /(x) cos nx je soda funkcija, f(x) sinnx pa je liha. Zato bodo Fourierjevi koeficienti sode funkcije f(x) enaki.Zato ima Fourierjeva vrsta sode funkcije obliko f(x) sin х - soda funkcija. Zato bomo imeli. Tako ima Fourierjeva vrsta lihe funkcije obliko Primer 1. Razširi funkcijo 4 v Fourierjevo vrsto na intervalu -x ^ x ^ n Ker je ta funkcija soda in izpolnjuje pogoje iz izreka 1, potem ima njegov Fourierjev niz obliko Poiščite Fourierjeve koeficiente. Če dvakrat uporabimo integracijo po delih, dobimo, da je torej Fourierjeva vrsta te funkcije videti takole: ali, v razširjeni obliki, Ta enakost velja za vsak x €, saj je v točkah x = ±ir vsota serija sovpada z vrednostmi funkcije f(x) = x2, saj sta grafa funkcije f(x) = x in vsota nastale serije podana na sl. Komentiraj. Ta Fourierjev niz nam omogoča, da poiščemo vsoto enega od konvergentnih numeričnih nizov, in sicer za x = 0 dobimo, da Primer 2. Razširimo funkcijo /(x) = x v Fourierjev niz na intervalu. Funkcija /(x) izpolnjuje pogoje iz izreka 1, zato jo lahko razširimo v Fourierjev niz, ki bo zaradi neparnosti te funkcije imel obliko Integriranje po delih najdemo Fourierjeve koeficiente. Fourierjeva serija te funkcije ima obliko. Ta enakost velja za vse x B v točkah x - ±t vsota Fourierjeve vrste ne sovpada z vrednostmi funkcije /(x) = x, saj je enaka Zunaj intervala [-*, i-] je vsota niza periodično nadaljevanje funkcije /(x) = x; njegov graf je prikazan na sl. 6. § 6. Razširitev funkcije, podane na intervalu, v vrsto po sinusih ali kosinusih Naj bo na intervalu podana omejena kosovno monotona funkcija /. Vrednosti te funkcije na intervalu 0| lahko nadalje opredelimo na različne načine. Na primer, lahko definirate funkcijo / na segmentu tc], tako da /. V tem primeru pravijo, da) "se razširi na segment 0] na enakomeren način"; njegova Fourierjeva vrsta bo vsebovala samo kosinuse. Če je funkcija /(x) definirana na intervalu [-l-, mc] tako, da je /(, potem je rezultat liha funkcija in potem pravijo, da je / »razširjen na interval [-*, 0] na nenavaden način"; v tem primeru bo Fourierjev niz vseboval samo sinuse. Tako lahko vsako omejeno kosovno monotono funkcijo /(x), definirano na intervalu, razširimo v Fourierjev niz tako v sinusih kot v kosinusih. Primer 1 Razširi funkcijo v Fourierjev niz: a) s kosinusi; b) s sinusi. M Ta funkcija s svojimi sodimi in lihimi nadaljevanji v segmentu |-x,0) bo omejena in po delih monotona. a) Razširite /(z) v odsek 0) a) Razširite j\x) v odsek (-π,0| na enakomeren način (slika 7), potem bo imela njegova Fourierjeva vrsta i obliko Π = 1 kjer sta Fourierjeva koeficienta enaka za. Zato b) Razširimo /(z) v segment [-x,0] na lih način (slika 8). Nato njegova Fourierjeva vrsta §7. Fourierjeva vrsta za funkcijo s poljubno periodo. Naj bo funkcija fix) periodična s periodo 21,1 ^ 0. Da jo razširimo v Fourierjevo vrsto na intervalu, kjer je I > 0, spremenimo spremenljivko tako, da nastavimo x = jt . Potem bo funkcija F(t) = / ^tj periodična funkcija argumenta t s periodo in jo je mogoče razširiti na segmentu v Fourierjev niz. Če se vrnemo k spremenljivki x, tj. nastavitvi, dobimo Vsi izreki veljavni za Fourierjevo vrsto periodičnih funkcij s periodo 2π , ostanejo veljavni za periodične funkcije s poljubno periodo 21. Zlasti ostaja veljaven tudi zadosten kriterij za razgradljivost funkcije v Fourierjevo vrsto. Primer 1. Razširite v Fourierjev niz periodično funkcijo s periodo 21, podano na intervalu [-/,/] s formulo (slika 9). Ker je ta funkcija enakomerna, ima njena Fourierjeva serija obliko Če najdene vrednosti Fourierjevih koeficientov zamenjamo v Fourierjevo serijo, dobimo. Omenimo eno pomembno lastnost periodičnih funkcij. Izrek 5. Če ima funkcija periodo T in je integrabilna, potem za poljubno število a velja enakost m. to pomeni, da ima integral segmenta, katerega dolžina je enaka periodi T, enako vrednost ne glede na položaj tega segmenta na številski osi. Pravzaprav naredimo spremembo spremenljivke v drugem integralu ob predpostavki. To daje in zato geometrijsko ta lastnost pomeni, da v primeru območja, zasenčenega na sl. 10 območij je med seboj enakih. Zlasti za funkcijo f(x) s periodo dobimo pri Razširitev v Fourierjevo vrsto sodih in lihih funkcij, razširitev funkcije, podane na intervalu, v vrsto v sinusnih ali kosinusnih Fourierjevih vrstah za funkcijo s poljubno perioda Kompleksni zapis Fourierjeve vrste Fourierjeva vrsta v splošnih ortogonalnih sistemskih funkcijah Fourierjeva vrsta v pravokotnem sistemu Minimalna lastnost Fourierjevih koeficientov Besselova neenakost Parsevalova enakost Zaprti sistemi Popolnost in zaprtost sistemov Primer 2. Funkcija x je periodična s periodo Zaradi nenavadnosti te funkcije, brez izračuna integralov, lahko trdimo, da je za katero koli. Dokazana lastnost zlasti kaže, da je mogoče Fourierjeve koeficiente periodične funkcije f(x) s periodo 21 izračunati z uporabo formul, kjer je a poljubno realno število (upoštevajte, da imata funkciji cos - in sin periodo 2/). Primer 3. Funkcijo, podano na intervalu s periodo 2x, razširite v Fourierjev niz (slika 11). 4 Poiščimo Fourierjeve koeficiente te funkcije. Če vstavimo formule, ugotovimo, da bo za Zato bo Fourierjeva vrsta izgledala takole: V točki x = jt (prekinitvena točka prve vrste) imamo §8. Kompleksno snemanje Fourierjevega niza V tem razdelku so uporabljeni nekateri elementi kompleksne analize (glejte poglavje XXX, kjer so vsa dejanja, izvedena tukaj s kompleksnimi izrazi, strogo utemeljena). Naj funkcija f(x) izpolnjuje zadostne pogoje za razširitev v Fourierjev niz. Nato ga lahko na odseku x] predstavimo z nizom oblike Z uporabo Eulerjevih formul Če te izraze zamenjamo v niz (1), namesto cos πx in sin φx bomo imeli. Vstavimo naslednji zapis. Potem bo niz (2) imel oblika Tako je Fourierjev niz (1) predstavljen v kompleksni obliki (3). Poiščimo izraze za koeficiente preko integralov. Imamo Podobno najdemo. Končne formule za с„, с_п in с lahko zapišemo takole: . . Koeficiente с„ imenujemo kompleksni Fourierjevi koeficienti funkcije. Za periodično funkcijo z obdobjem bo kompleksna oblika Fourierove vrste v obliki, kjer so koeficienti Cn izračunani z uporabo formul. Konvergenca nizov (3 ) in (4) razumemo takole: seriji (3) in (4) pravimo konvergentni za dano vrednost g, če obstajajo omejitve Primer. Razširite periodno funkcijo v kompleksno Fourierjevo vrsto. Ta funkcija izpolnjuje zadostne pogoje za razširitev v Fourierjevo vrsto. Poiščimo kompleksne Fourierjeve koeficiente te funkcije. Imamo za liho za sodo n ali, na kratko. Če zamenjamo vrednosti), končno dobimo Upoštevajte, da lahko to vrsto zapišemo tudi na naslednji način: Fourierjeva vrsta za splošne ortogonalne sisteme funkcij 9.1. Ortogonalni sistemi funkcij Označimo z množico vseh (realnih) funkcij, definiranih in integrabilnih na intervalu [a, 6] s kvadratom, torej tistih, za katere obstaja integral, zlasti vse zvezne funkcije f(x). na intervalu [a, 6], pripadajo 6], vrednosti njihovih Lebesguevih integralov pa sovpadajo z vrednostmi Riemannovih integralov. Opredelitev. Sistem funkcij, kjer je, se imenuje pravokoten na intervalu [a, b\, če pogoj (1) predpostavlja zlasti, da nobena od funkcij ni enaka nič. Integral razumemo v Lebesgueovem smislu. in kvantiteto imenujemo norma funkcije.Če imamo v ortogonalnem sistemu za katerikoli n, potem sistem funkcij imenujemo ortonormiran. Če je sistem (y>„(x)) pravokoten, potem sistem Primer 1. Trigonometrični sistem je pravokoten na odseku. Sistem funkcij je ortonormiran sistem funkcij na Primer 2. Kosinusni sistem in sinusni sistem sta ortonormirana. Vpišimo oznako, da so pravokotni na intervalu (0, f|, vendar ne ortonormirani (za I Ф- 2). Ker so njihove norme COS Primer 3. Polinome, določene z enakostjo, imenujemo Legendrovi polinomi (polinomi). Za n = 0 imamo Lahko se dokaže, da funkcije tvorijo ortonormiran sistem funkcij na intervalu. Pokažimo na primer ortogonalnost Legendrovih polinomov. Naj bo m > n. V tem primeru integriramo n-krat z delov, najdemo, saj za funkcijo t/m = (z2 - I)m vsi odvodi do vključno reda m - I izničijo na koncih segmenta [-1,1). Opredelitev. Sistem funkcij (pn(x)) imenujemo pravokoten na intervalu (a, b) s previsom p(x), če: 1) za vse n = 1,2,... obstajajo integrali. Tukaj je predpostavimo, da je utežna funkcija p(x) definirana in pozitivna povsod na intervalu (a, b) z možno izjemo končnega števila točk, kjer lahko p(x) izniči. Po izvedbi diferenciacije v formuli (3) ugotovimo. Lahko se pokaže, da so Chebyshev-Hermitovi polinomi pravokotni na intervalu Primer 4. Sistem Besselovih funkcij (jL(pix)^ je pravokoten na intervalnih ničlah Besselove funkcije Primer 5. Oglejmo si Chebyshev-Hermitove polinome , ki ga lahko definiramo z enakostjo. Fourierjeva vrsta v ortogonalnem sistemu. Naj obstaja pravokoten sistem funkcij v intervalu (a, 6) in naj vrsta (cj = const) konvergira na tem intervalu k funkciji f(x): Množenje obeh strani zadnje enakosti by - fixed) in integriramo po x od a do 6, zaradi ortogonalnosti sistema dobimo, da ima ta operacija na splošno čisto formalen značaj. Vendar pa je v nekaterih primerih, na primer, ko niz (4) enakomerno konvergira, so vse funkcije zvezne in je interval (a, 6) končen, ta operacija zakonita. Toda za nas je zdaj pomembna formalna razlaga. Torej, naj bo dana funkcija. Sestavimo števila c* po formuli (5) in zapišimo. Vrst na desni strani imenujemo Fourierjeva vrsta funkcije f(x) glede na sistem (^n(i)). Števili Cn imenujemo Fourierjevi koeficienti funkcije f(x) glede na ta sistem. Znak ~ v formuli (6) pomeni le, da so števila Cn povezana s funkcijo f(x) s formulo (5) (ne predpostavlja se, da vrsta na desni sploh konvergira, še manj pa konvergira k funkciji f (x)). Zato se seveda postavlja vprašanje: kakšne so lastnosti te serije? V kakšnem smislu "predstavlja" funkcijo f(x)? 9.3. Konvergenca v povprečju Definicija. Zaporedje konvergira k elementu ] v povprečju, če je norma v prostoru. Izrek 6. Če zaporedje ) konvergira enakomerno, potem konvergira v povprečju. M Naj zaporedje ()) enakomerno konvergira na intervalu [a, b] k funkciji /(x). To pomeni, da za vse, za vse dovolj velike n, velja Torej, iz česar sledi naša trditev. Obratno ne drži: zaporedje () lahko v povprečju konvergira k /(x), vendar ni enakomerno konvergentno. Primer. Razmislite o zaporedju nx. Zlahka je videti, da Toda ta konvergenca ni enakomerna: obstaja na primer e, tako da ne glede na to, kako velik je n, na intervalnih kosinusih Fourierjeva vrsta za funkcijo s poljubno periodo Kompleksna predstavitev Fourierjeve vrste Fourierjeve vrste za splošne ortogonalne sisteme funkcij Fourierjeve vrste za pravokotni sistem Minimalna lastnost Fourierjevih koeficientov Besselova neenakost Parsevalova enakost Zaprti sistemi Popolnost in zaprtost sistemov in naj S c* označimo Fourierjeve koeficiente funkcije /(x ) z ortonormiranim sistemom b Razmislite o linearni kombinaciji, kjer je n ^ 1 fiksno celo število, in poiščite vrednosti konstant, pri katerih ima integral najmanjšo vrednost. Zapišimo jo podrobneje Integrirajo člen za členom, zaradi ortonormiranosti sistema dobimo, da sta prva dva člena na desni strani enačbe (7) neodvisna, tretji člen pa je nenegativen. Zato ima integral (*) minimalno vrednost pri ak = sk Integral imenujemo povprečna kvadratna aproksimacija funkcije /(x) z linearno kombinacijo Tn(x). Tako povprečni kvadratni približek funkcije /\ zavzame najmanjšo vrednost, ko. ko je Tn(x) 71. delna vsota Fourierjeve vrste funkcije /(x) nad sistemom (. Če nastavimo ak = sk, iz (7) dobimo Enakost (9) imenujemo Besselova identiteta. Ker je njena leva stran nenegativna, potem iz nje sledi Besselova neenakost. Ker sem tukaj poljubno, lahko Besselovo neenakost predstavimo v okrepljeni obliki, tj. . Ker je sistem ortonormiran na intervalu [-x, m], potem neenakost (10), prevedena v običajni zapis trigonometričnega Fourierovega niza, daje relacijo do, ki velja za vsako funkcijo /(x) z integrabilnim kvadratom. Če je f2(x) integrabilen, potem zaradi nujnega pogoja za konvergenco vrste na levi strani neenačbe (11) dobimo to. Parsevalova enakost Za nekatere sisteme (^„(x)) lahko znak neenakosti v formuli (10) nadomestimo (za vse funkcije f(x) 6 ×) z znakom enačaja. Nastala enakost se imenuje Parseval-Steklova enakost (pogoj popolnosti). Besselova identiteta (9) nam omogoča, da pogoj (12) zapišemo v ekvivalentni obliki.Izpolnjenost pogoja popolnosti torej pomeni, da delne vsote Sn(x) Fourierjeve vrste funkcije /(x) konvergirajo k funkciji /(x) v povprečju, tj. po normi prostora 6]. Opredelitev. Ortonormiran sistem ( se imenuje popoln v b2[ау b], če je vsako funkcijo mogoče v povprečju s poljubno natančnostjo približati z linearno kombinacijo oblike c dovolj veliko številoče za katero koli funkcijo /(x) € b2[a, b\ in za kateri koli e > 0 obstajajo naravno število nq in števila a\, a2y ..., tako da Ne Iz zgornjega razmišljanja sledi izrek 7. Če je z ortonormacijo sistem ) popoln v prostoru, Fourierjeva vrsta katere koli funkcije / za ta sistem v povprečju konvergira k f(x), to je po normi. Lahko se pokaže, da je trigonometrični sistem popoln v prostor To implicira izjavo. Izrek 8. Če funkcija /o njena trigonometrična Fourierjeva vrsta konvergira k njej v povprečju. 9.5. Zaprti sistemi. Popolnost in zaprtost sistemov Definicija. Ortonormiran sistem funkcij \ imenujemo zaprt, če v prostoru Li\a, b) ni nobene neničelne funkcije, pravokotne na vse funkcije V prostoru L2\a, b\ koncepta popolnosti in zaprtosti ortonormiranih sistemov sovpadata. Vaje 1. Razširi funkcijo 2 v Fourierjev niz v intervalu (-i-, x) 2. Razširi funkcijo v Fourierjev niz v intervalu (-tr, tr) 3. Razširi funkcijo 4 v Fourierjev niz v interval (-tr, tr) v Fourierjev niz v intervalu (-jt, tr) funkcija 5. Razširi funkcijo f(x) = x + x v Fourierjev niz v intervalu (-tr, tr). 6. Razširi funkcijo n v Fourierjev niz v intervalu (-jt, tr) 7. Razširi funkcijo /(x) = sin2 x v Fourierjev niz v intervalu (-tr, x). 8. Razširi funkcijo f(x) = y v Fourierjev niz v intervalu (-tr, jt) 9. Razširi funkcijo f(x) = | greh x|. 10. Razširi funkcijo f(x) = § v Fourierjev niz v intervalu (-π-, π). 11. Funkcijo f(x) = sin § razširimo v Fourierjev niz v intervalu (-tr, tr). 12. Funkcijo f(x) = n -2x, podano v intervalu (0, x), razširimo v Fourierjev niz in jo razširimo v interval (-x, 0): a) na sodi način; b) na čuden način. 13. Funkcijo /(x) = x2, podano v intervalu (0, x), razširite v Fourierjev niz po sinusih. 14. Funkcijo /(x) = 3, podano v intervalu (-2,2), razširite v Fourierjev niz. 15. Funkcijo f(x) = |x|, podano v intervalu (-1,1), razširite v Fourierjev niz. 16. Funkcijo f(x) = 2x, podano v intervalu (0,1), razširite v Fourierjev niz po sinusih. Fourierjeva vrsta periodičnih funkcij s periodo 2π.
Fourierjeva vrsta nam omogoča preučevanje periodičnih funkcij tako, da jih razgradimo na komponente. Izmenični tokovi in napetosti, pomiki, hitrosti in pospeški ročičnih mehanizmov ter akustični valovi so tipični praktični primeri uporabe periodičnih funkcij v inženirskih izračunih. Razširitev v Fourierjev niz temelji na predpostavki, da imajo vsi praktični pomen funkcije v intervalu -π ≤x≤ π lahko izrazimo v obliki konvergentnih trigonometričnih vrst (vrsta se šteje za konvergentno, če konvergira zaporedje delnih vsot, sestavljenih iz njenih členov): Standardni (=navadni) zapis skozi vsoto sinx in cosx f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+..., kjer so a o, a 1,a 2,...,b 1,b 2,.. realne konstante, tj. Pri čemer se za območje od -π do π koeficienti Fourierjeve vrste izračunajo po formulah: Koeficienti a o , a n in b n se imenujejo Fourierjevi koeficienti, in če jih je mogoče najti, se pokliče serija (1). poleg Fourierja, ki ustreza funkciji f(x). Za niz (1) imenujemo člen (a 1 cosx+b 1 sinx) prvi oz osnovni harmonik, Drug način za pisanje serije je uporaba relacije acosx+bsinx=csin(x+α) f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n) Kjer je a o konstanta, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 so amplitude različnih komponent in je enako a n =arctg a n /b n. Za vrsto (1) se člen (a 1 cosx+b 1 sinx) ali c 1 sin(x+α 1) imenuje prvi oz. osnovni harmonik,(a 2 cos2x+b 2 sin2x) ali c 2 sin(2x+α 2) se imenuje drugi harmonik in tako naprej. Za natančno predstavitev kompleksnega signala je običajno potrebno neskončno število izrazov. Vendar je v mnogih praktičnih problemih dovolj, da upoštevamo samo prvih nekaj členov. Fourierjeva vrsta neperiodičnih funkcij s periodo 2π.
Razširitev neperiodičnih funkcij. Če je funkcija f(x) neperiodična, to pomeni, da je ni mogoče razširiti v Fourierjev niz za vse vrednosti x. Vendar pa je mogoče definirati Fourierjev niz, ki predstavlja funkcijo v poljubnem območju širine 2π. Glede na neperiodično funkcijo je mogoče konstruirati novo funkcijo tako, da izberete vrednosti f(x) znotraj določenega območja in jih ponovite zunaj tega območja v intervalih 2π. Zaradi nova funkcija je periodičen s periodo 2π, ga je mogoče razširiti v Fourierjev niz za vse vrednosti x. Na primer, funkcija f(x)=x ni periodična. Če pa jo je treba razširiti v Fourierjev niz v intervalu od o do 2π, se izven tega intervala sestavi periodična funkcija s periodo 2π (kot je prikazano na spodnji sliki). Za neperiodične funkcije, kot je f(x)=x, je vsota Fourierjevega niza enaka vrednosti f(x) v vseh točkah v danem območju, vendar ni enaka f(x) za točke izven obsega. Za iskanje Fourierjeve vrste neperiodične funkcije v območju 2π se uporablja ista formula Fourierjevih koeficientov. Sode in lihe funkcije.
Pravijo, da je funkcija y=f(x) celo, če je f(-x)=f(x) za vse vrednosti x. Grafi sodih funkcij so vedno simetrični glede na os y (to pomeni, da so zrcalne slike). Dva primera sodih funkcij: y=x2 in y=cosx. Pravijo, da je funkcija y=f(x) Čuden,če je f(-x)=-f(x) za vse vrednosti x. Grafi lihih funkcij so vedno simetrični glede na izvor. Mnoge funkcije niso niti sode niti lihe. Razširitev v Fourierjev niz v kosinuse.
Fourierjeva vrsta sode periodične funkcije f(x) s periodo 2π vsebuje samo kosinusne člene (tj. ne vsebuje sinusnih členov) in lahko vključuje stalni član. torej kje so koeficienti Fourierove vrste,
Fourierjeva vrsta lihe periodične funkcije f(x) s periodo 2π vsebuje samo člene s sinusi (to pomeni, da ne vsebuje členov s kosinusi). torej kje so koeficienti Fourierove vrste, Fourierjeva vrsta na pol cikla.
Če je funkcija definirana za obseg, recimo od 0 do π, in ne le od 0 do 2π, jo je mogoče razširiti v vrsto samo v sinusih ali samo v kosinusih. Nastala Fourierjeva vrsta se imenuje blizu Fourierja na pol cikla. Če želite dobiti razgradnjo Fourierjev polciklični kosinus funkcije f(x) v območju od 0 do π, potem je treba zgraditi sodo periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je soda funkcija simetrična glede na os f(x), narišemo premico AB, kot je prikazano na sliki. spodaj. Če predpostavimo, da je zunaj obravnavanega intervala nastala trikotna oblika periodična s periodo 2π, potem končni graf izgleda takole: na sl. spodaj. Ker moramo kot prej pridobiti Fourierjevo razširitev v kosinusih, izračunamo Fourierjeva koeficienta a o in a n Če morate dobiti Fourierjeva sinusna ekspanzija polcikla funkcije f(x) v območju od 0 do π, potem je treba zgraditi liho periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je liha funkcija simetrična glede na izvor, sestavimo premico CD, kot je prikazano na sl. Če predpostavimo, da je zunaj obravnavanega intervala nastali žagasti signal periodičen s periodo 2π, potem ima končni graf obliko, prikazano na sl. Ker moramo kot prej dobiti Fourierjevo razširitev polcikla v smislu sinusov, izračunamo Fourierjev koeficient. b Fourierjeva vrsta za poljuben interval.
Razširitev periodične funkcije s periodo L. Periodična funkcija f(x) se ponavlja, ko x narašča za L, tj. f(x+L)=f(x). Prehod s predhodno obravnavanih funkcij s periodo 2π na funkcije s periodo L je dokaj preprost, saj ga lahko izvedemo s spremembo spremenljivke. Za iskanje Fourierjeve vrste funkcije f(x) v območju -L/2≤x≤L/2 uvedemo novo spremenljivko u, tako da ima funkcija f(x) periodo 2π glede na u. Če je u=2πx/L, potem je x=-L/2 za u=-π in x=L/2 za u=π. Naj bo tudi f(x)=f(Lu/2π)=F(u). Fourierjeva vrsta F(u) ima obliko (Meje integracije lahko nadomestimo s poljubnim intervalom dolžine L, na primer od 0 do L) Fourierjeva vrsta na polciklu za funkcije, določene v intervalu L≠2π.
Za zamenjavo u=πх/L interval od x=0 do x=L ustreza intervalu od u=0 do u=π. Posledično lahko funkcijo razširimo v vrsto samo v kosinusih ali samo v sinusih, tj. V Fourierjeva vrsta na pol cikla. Kosinusna ekspanzija v območju od 0 do L ima obliko Fourierjeve vrste so predstavitev poljubne funkcije z določeno periodo v obliki vrste. IN splošni pogled ta odločitev se imenuje dekompozicija elementa v ortogonalni bazi. Razširitev funkcij v Fourierjev niz je dokaj močno orodje za reševanje različnih problemov zaradi lastnosti te transformacije med integracijo, diferenciacijo, pa tudi premikanjem izrazov z argumentom in konvolucijo. Oseba, ki ni seznanjena z višjo matematiko, pa tudi z deli francoskega znanstvenika Fourierja, najverjetneje ne bo razumela, kaj so te "serije" in za kaj so potrebne. Medtem je ta preobrazba postala precej integrirana v naša življenja. Ne uporabljajo ga le matematiki, ampak tudi fiziki, kemiki, zdravniki, astronomi, seizmologi, oceanografi in mnogi drugi. Oglejmo si pobliže tudi dela velikega francoskega znanstvenika, ki je prišel do odkritja, ki je bilo pred svojim časom. Fourierjeve vrste so ena od metod (poleg analize in drugih).Ta proces se zgodi vsakič, ko oseba sliši zvok. Naše uho samodejno transformira osnovne delce v elastičnem mediju v vrste (vzdolž spektra) zaporednih stopenj glasnosti za tone različnih višin. Nato možgani te podatke spremenijo v zvoke, ki so nam znani. Vse to se dogaja brez naše želje ali zavesti, samo od sebe, a da bi razumeli te procese, bo potrebnih nekaj let študija višje matematike. Fourierjevo transformacijo je mogoče izvesti z analitičnimi, numeričnimi in drugimi metodami. Fourierjeve vrste se nanašajo na numerično metodo razčlenitve kakršnih koli nihajnih procesov - od oceanske plime in svetlobnih valov do ciklov sončne (in drugih astronomskih objektov) aktivnosti. Z uporabo teh matematičnih tehnik lahko analizirate funkcije, ki predstavljajo vse nihajne procese kot niz sinusnih komponent, ki se premikajo od minimuma do maksimuma in nazaj. Fourierjeva transformacija je funkcija, ki opisuje fazo in amplitudo sinusoide, ki ustreza določeni frekvenci. Ta proces se lahko uporablja za reševanje zelo kompleksnih enačb, ki opisujejo dinamične procese, ki nastanejo pod vplivom toplotne, svetlobne ali električne energije. Poleg tega Fourierjeve vrste omogočajo izolacijo konstantnih komponent v kompleksnih oscilacijskih signalih, kar omogoča pravilno interpretacijo eksperimentalnih opazovanj, pridobljenih v medicini, kemiji in astronomiji. Ustanovitelj te teorije je francoski matematik Jean Baptiste Joseph Fourier. Ta preobrazba je bila pozneje poimenovana po njem. Sprva je znanstvenik s svojo metodo preučeval in razlagal mehanizme toplotne prevodnosti - širjenje toplote v trdne snovi. Fourier je predlagal, da se lahko začetna nepravilna porazdelitev razgradi na preproste sinusoide, od katerih bo imela vsaka svoj minimum in maksimum temperature ter svojo fazo. V tem primeru bo vsaka taka komponenta izmerjena od minimuma do maksimuma in nazaj. Matematična funkcija, ki opisuje zgornje in spodnje vrhove krivulje ter fazo vsakega od harmonikov, se imenuje Fourierjeva transformacija izraza porazdelitve temperature. Avtor teorije je združil splošna funkcija porazdelitev, ki jo je težko matematično opisati, v zelo priročno vrsto kosinusa in sinusa, ki skupaj dajeta prvotno porazdelitev. Znanstvenikovi sodobniki - vodilni matematiki zgodnjega devetnajstega stoletja - te teorije niso sprejeli. Glavni ugovor je bila Fourierjeva trditev, da je diskontinuirano funkcijo, ki opisuje ravno črto ali diskontinuirano krivuljo, mogoče predstaviti kot vsoto sinusnih izrazov, ki so zvezni. Kot primer upoštevajte Heavisideov korak: njegova vrednost je nič na levi strani prekinitve in ena na desni. Ta funkcija opisuje odvisnost električnega toka od začasne spremenljivke, ko je tokokrog sklenjen. Takratni sodobniki teorije še nikoli niso naleteli na podobno situacijo, kjer bi bil diskontinuiran izraz opisan s kombinacijo zveznih, običajnih funkcij, kot so eksponentna, sinusna, linearna ali kvadratna. Navsezadnje, če je imel matematik prav v svojih izjavah, potem lahko s seštevanjem neskončnega trigonometričnega Fourierovega niza dobimo natančno predstavitev stopenjskega izraza, tudi če ima veliko podobnih korakov. Na začetku devetnajstega stoletja se je takšna izjava zdela absurdna. Toda kljub vsem dvomom so številni matematiki razširili obseg proučevanja tega pojava in ga presegli študij toplotne prevodnosti. Vendar pa je večino znanstvenikov še naprej mučilo vprašanje: "Ali se lahko vsota sinusne serije konvergira k natančni vrednosti diskontinuirane funkcije?" Vprašanje konvergence se pojavi vedno, ko je treba sešteti neskončno vrsto števil. Da bi razumeli ta pojav, razmislite o klasičnem primeru. Vam bo kdaj uspelo doseči steno, če bo vsak naslednji korak za polovico manjši od prejšnjega? Recimo, da ste dva metra od cilja, prvi korak vas pripelje do polovice poti, naslednji vas pripelje do tričetrt, po petem pa boste prehodili že skoraj 97 odstotkov poti. Vendar ne glede na to, koliko korakov naredite, ne boste dosegli zastavljenega cilja v strogem matematičnem smislu. Z uporabo numeričnih izračunov je mogoče dokazati, da se je na koncu mogoče približati na dano razdaljo. Ta dokaz je enakovreden dokazovanju, da bo vsota polovice, ene četrtine itd. težila k enotnosti. To vprašanje se je znova pojavilo ob koncu devetnajstega stoletja, ko so poskušali s Fourierjevimi vrstami napovedati intenzivnost plimovanja. V tem času je lord Kelvin izumil instrument, ki je bil analogna računalniška naprava, ki je vojaškim in trgovskim mornarjem omogočala sledenje temu naravni pojav. Ta mehanizem je določil sklope faz in amplitud iz tabele višin plime in ustreznih časovnih točk, skrbno izmerjenih v danem pristanišču skozi vse leto. Vsak parameter je bil sinusna komponenta izraza višine plime in je bil ena od rednih komponent. Meritve so bile vnesene v računski instrument Lorda Kelvina, ki je sintetiziral krivuljo, ki je napovedala višino vode kot funkcijo časa za naslednje leto. Kmalu so se podobne krivulje izrisale za vsa pristanišča sveta. Takrat se je zdelo očitno, da lahko napovedovalec plimskih valov z velikim številom elementov štetja izračuna veliko število faz in amplitud ter tako zagotovi natančnejše napovedi. Vendar se je izkazalo, da tega vzorca ni opaziti v primerih, ko je izraz plimovanja, ki bi ga bilo treba sintetizirati, vseboval oster skok, to je bil diskontinuiran. Če v napravo vnesemo podatke iz tabele časovnih trenutkov, ta izračuna več Fourierjevih koeficientov. Prvotna funkcija je obnovljena zahvaljujoč sinusnim komponentam (v skladu z najdenimi koeficienti). Neskladje med izvirnim in rekonstruiranim izrazom je mogoče izmeriti na kateri koli točki. Pri ponovnih izračunih in primerjavah je jasno, da se vrednost največje napake ne zmanjša. Vendar so lokalizirani v območju, ki ustreza točki diskontinuitete, na kateri koli drugi točki pa težijo k ničli. Leta 1899 je ta rezultat teoretično potrdil Joshua Willard Gibbs z univerze Yale. Fourierjeva analiza ni uporabna za izraze, ki vsebujejo neskončno število konic v določenem intervalu. Na splošno Fourierjeva vrsta, če je prvotna funkcija predstavljena z rezultatom realne fizična razsežnost, vedno konvergirajo. Vprašanja o konvergenci tega procesa za posebne razrede funkcij so privedla do nastanka novih vej v matematiki, na primer teorije posplošenih funkcij. Povezujejo jo z imeni, kot so L. Schwartz, J. Mikusinski in J. Temple. V okviru te teorije je bila ustvarjena jasna in natančna teoretična podlaga za izraze, kot sta Diracova delta funkcija (opisuje območje enega samega območja, koncentriranega v neskončno majhni okolici točke) in Heavisideov "korak". Zahvaljujoč temu delu so Fourierjeve vrste postale uporabne za reševanje enačb in problemov, ki vključujejo intuitivne pojme: točkasti naboj, točkasta masa, magnetni dipoli in koncentrirana obremenitev na žarku. Fourierjeve vrste se v skladu z načeli interference začnejo z razgradnjo kompleksnih oblik na preprostejše. Na primer, spremembo toplotnega toka razložimo s prehodom skozi različne ovire iz toplotnoizolacijskega materiala nepravilne oblike ali spremembo površine zemlje - potres, sprememba orbite nebesno telo- vpliv planetov. Takšne enačbe, ki opisujejo preproste klasične sisteme, je praviloma enostavno rešiti za vsak posamezen val. Fourier je pokazal, da je mogoče preproste rešitve sešteti tudi za rešitve bolj zapletenih problemov. V matematičnem smislu so Fourierjevi nizi tehnika za predstavitev izraza kot vsote harmonikov - kosinusa in sinusa. Zato je ta analiza znana tudi kot "harmonična analiza". Pred nastankom računalniške tehnologije je bila Fourierjeva tehnika najboljše orožje v arzenalu znanstvenikov pri delu z valovno naravo našega sveta. Fourierjeva vrsta v kompleksni obliki omogoča reševanje ne le preprostih problemov, ki jih je mogoče neposredno uporabiti z Newtonovimi zakoni mehanike, temveč tudi temeljne enačbe. Večino odkritij Newtonove znanosti v devetnajstem stoletju je omogočila le Fourierjeva tehnika. Z razvojem računalnikov so se Fourierove transformacije dvignile na kvalitativno raven nova raven. Ta tehnika je trdno uveljavljena na skoraj vseh področjih znanosti in tehnologije. Primer sta digitalni avdio in video. Njegovo izvajanje je postalo mogoče le zahvaljujoč teoriji, ki jo je razvil francoski matematik v začetku devetnajstega stoletja. Tako je Fourierjeva serija v kompleksni obliki omogočila preboj v študiji vesolje. Poleg tega je vplival na študij fizike polprevodniških materialov in plazme, mikrovalovne akustike, oceanografije, radarja in seizmologije. V matematiki je Fourierjeva vrsta način predstavitve poljubnih kompleksnih funkcij kot vsote enostavnejših. V splošnih primerih je lahko število takih izrazov neskončno. Poleg tega, bolj kot je njihovo število upoštevano pri izračunu, bolj natančen je končni rezultat. Najpogosteje se kot najenostavnejše uporabljajo trigonometrične funkcije kosinusa ali sinusa. V tem primeru se Fourierjeve vrste imenujejo trigonometrične, rešitev takih izrazov pa harmonična ekspanzija. Ta metoda igra pomembno vlogo v matematiki. Prvič, trigonometrična vrsta zagotavlja sredstvo za prikaz in tudi preučevanje funkcij; je glavni aparat teorije. Poleg tega vam omogoča reševanje številnih problemov matematične fizike. Končno je ta teorija prispevala k razvoju številnih zelo pomembnih vej matematične znanosti (teorija integralov, teorija periodičnih funkcij). Poleg tega je služil kot izhodišče za razvoj naslednjih funkcij realne spremenljivke in postavil temelje za harmonično analizo.
(2.18)
(2.19)3.2. Trigonometrične serije. Fourierjevi koeficienti
.
(2)
, potem je tudi vsota niza, če konvergira, periodična funkcija s periodo 
.
.
(3)
, lahko njegove koeficiente določite z uporabo formul:
, 
,
.
(4)3.3. Konvergenca Fourierjevih vrst
-periodična funkcija, tj. Za takšno funkcijo lahko vedno sestavite Fourierjev niz. Toda ali bo ta serija konvergirala k funkciji f(x)
in pod kakšnimi pogoji?
-periodična funkcija f(x)
je po delih gladka 
. Potem se njegova Fourierjeva vrsta konvergira v f(x)
na vsaki njeni točki kontinuitete in na vrednost 0,5(f(x+0)+
f(x-0))
na prelomni točki.
.
, najdemo Fourierjeve koeficiente:
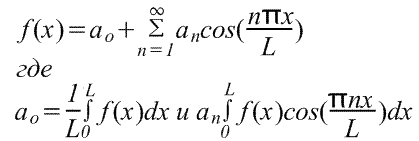
Človek in Fourierjeva transformacija
Več o Fourierjevi transformaciji
Zgodovinska referenca
Načelo preobrazbe in pogledi sodobnikov
Kaj je zmedlo francoske matematike glede Fourierjeve teorije?
Konvergenca Fourierjevih vrst: primer
Vprašanje konvergence: Drugi prihod ali Naprava Lorda Kelvina
Kaj pa, če je proces moten zaradi diskontinuirane funkcije?
Konvergenca Fourierjevih vrst in razvoj matematike nasploh
Fourierjeva metoda
Fourierjeva vrsta - idealna tehnika pred "računalniško dobo"
Fourierjeva vrsta danes
Trigonometrična Fourierjeva vrsta
