孤立特異点を見つける方法。ローラン級数孤立特異点とその分類

自動 03.10.2020

自動

2 つの自律微分方程式系によって記述されるモデル。

位相面。位相の肖像画。イソクリン法。主要な等傾斜線。静止状態の安定性。線形システム。特異点の種類: ノード、サドル、焦点、中心。例：化学反応最初の注文。

生物学的システムの特性の定性モデリングに関する最も興味深い結果は、2 つの微分方程式のモデルを使用して得られました。これにより、次の方法を使用した定性的研究が可能になります。 位相面。 2 つの自律常微分方程式からなる系を考えます。全体像

(4.1)

P(x,y)、Q(x,y)- いくつかのドメインで定義された連続関数 Gユークリッド平面 ( x、y- デカルト座標) であり、この領域に最初の次数以上の連続導関数が存在します。

地域 G無制限または制限付きのいずれかになります。変数の場合 x、y特定の生物学的意味（物質の濃度、種の数）を持っていることがほとんどです。 Gは右半平面の正の象限を表します。

0 £ ×< ¥ ,0 £ y< ¥ .

物質の濃度や種の数は、容器の体積や生息地の面積によって上から制限されることもあります。この場合、変数の範囲は次の形式になります。

0 £ ×< x 0 , 0 £ y< y 0 .

変数 x、y系の各状態が変数値のペアに対応するように、連立方程式 (4.1) に従って時間変化します ( x、y).

逆に、変数の各ペア ( x、y) はシステムの特定の状態に対応します。

変数の値がプロットされる座標軸を持つ平面を考えます。 x、y。あらゆる点 Mこの平面はシステムの特定の状態に対応します。 この平面は位相平面と呼ばれ、システムのすべての状態の全体を表します。点 M(x,y) は代表点または代表点と呼ばれます。

最初の瞬間にしましょう t=t代表点の0座標 M 0 (×(t 0)、y(t 0)). 次の瞬間にも t変数の値の変化に応じて代表点が移動します ×(t)、y(t). ポイントの貯め方 M(×(t)、y(t)) 位相平面上で、その位置は時間の経過とともに変数が変化する過程におけるシステムの状態に対応します。 x(t), y(t)式 (4.1) によれば、と呼ばれます。 位相の軌跡。

変数のさまざまな初期値に対する位相軌跡のセットにより、システムの目に見える「ポートレート」が得られます。工事 位相ポートレート変数の変化の性質について結論を引き出すことができます x、y元の方程式系の解析解の知識がなくても(4.1).

位相ポートレートを描くには、位相平面の各点でシステム軌道の方向のベクトル場を構築する必要があります。インクリメントの設定D t>0、対応する増分を取得します D ×そして D y式から:

D x=P(x,y)D t,

D y=Q(x,y)D t.

ベクトルの方向 ダイ/DX時点で（ x、y) 関数の符号に依存します P(x, y)、Q(x, y)そして、テーブルで与えることができます:

P(x,y)>0、Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

この方程式の解 y = y(x、c), または暗黙的に F(x、y)=c、どこと– 積分定数、式 (4.2) の積分曲線の族を与える – 位相軌道飛行機上のシステム (4.1) x、y.

アイソクライン法

彼らが使用する位相ポートレートを構築するために 等傾斜法 –積分曲線と特定の角度で交差する線が位相平面上に描かれます。等傾斜方程式は (4.2) から簡単に得られます。入れましょう

どこあ– ある一定の値。意味あ位相軌道に対する接線の傾斜角の接線を表し、次の値を取ることができます –¥ +に ¥ 。代わりに代用する ダイ/DX(4.2) の量あ等傾斜方程式が得られます。

.(4.3)

式 (4.3) は、平面の各点で、対応する積分曲線に対する一意の接線を定義します。ただし、次の点は除きます。 P(x,y)= 0、Q (x、y) = 0 、微分の値が不確実になるため、接線の方向が不確実になります。

この点はすべての等傾斜線の交点です - 特別な点。その中で、変数の時間導関数は同時に消滅します。 ×そして y.

したがって、特異点では、変数の変化率はゼロになります。したがって、位相軌跡の微分方程式 (4.2) の特異点は、次のようになります。 システムの定常状態(4.1)、その座標は変数の定常値です x、y。

特に興味深いのは、 主なアイソクライン:

dy/dx=0、P(x、y)=0 – 水平接線の等傾斜線と

dy/dx=¥ 、Q(x、y)=0 – 垂直接線の等傾斜線。

主要な等傾斜線を作成し、その交点を見つけることによって (x,y)、その座標は次の条件を満たします。

これにより、位相軌道の接線の方向が不確かな、位相平面のすべての等傾斜線の交点が見つかります。これ - 特異点、対応する システムの定常状態(図4.2)。

システム (4.1) には、位相平面上の主等傾斜線の交点と同じ数の定常状態があります。

各フェーズの軌跡は、同じ状態を通過する動的システムの一連の動きに対応し、時間カウントの開始点のみが互いに異なります。

コーシーの定理の条件が満たされる場合、空間内の各点を介して x、y、t積分曲線は 1 つだけです。自律性により、位相軌道にも同じことが当てはまります。単一の位相軌道が位相平面の各点を通過します。

定常状態の安定性

システムが平衡状態にあるとします。

次に、代表点はシステムの特異点の 1 つに配置されます。定義により、特異点では次のようになります。

特異点が安定しているかどうかは、代表点が静止状態からわずかにずれているかどうかで決まります。 2 つの方程式系に関連して、言語の安定性の定義e, dこのように見えます。

平衡状態からの逸脱が所定の範囲内にある場合、平衡状態は安定しています。 (e )エリアを指定できます d (e )、平衡状態を囲み、領域内で始まる軌道がないという特性を持っています。 d 、決して国境に到達することはありません e 。 (図4.4)

大規模なクラスのシステムの場合 - ラフなシステム – 方程式の形を少し変えても挙動の性質は変わらないため、定常状態付近の挙動の種類に関する情報は、元の式ではなく単純化された式を調べることで得られます。 線形化されたシステム。

線形システム。

2人体制を考えてみましょう線形方程式:

.(4.4)

ここ a、b、c、d- 定数、 x、y- 位相平面上のデカルト座標。

次の形式で一般的な解決策を探します。

.(4.5)

これらの式を (4.4) に代入し、次のように削減してみましょう。 e 私 t:

(4.6)

未知数を含む代数方程式系 (4.6) A、Bは、未知数の係数で構成される行列式が 0 に等しい場合にのみ、非ゼロの解を持ちます。

この行列式を展開すると、システムの特性方程式が得られます。

.(4.7)

この方程式を解くと指数値が得られます私 1,2 、ゼロ以外の値が可能ですあそして B方程式 (4.6) の解。これらの意味は、

.(4.8)

根号式が負の場合、私 1,2 複素共役数。方程式 (4.7) の両方の根がゼロ以外の実部を持ち、複数の根が存在しないと仮定します。この場合、システム (4.4) の一般解は、指数と指数の線形結合として表すことができます。私 1 , 私 2 :

(4.9)

位相平面上のシステムの可能な軌道の性質を分析するには、次を使用します。 線形同次座標変換、それはシステムを次のように導くでしょう 正規形:

,(4.10)

元のシステム (4.4) と比較して、位相平面上でより便利な表現が可能になります。新しいコーディネートをご紹介しましょうξ , η 式によると：

(4.1)

線形代数の過程から、ゼロへの不等式の場合、実部は私 1 , 私 2 元の系 (4.4) は、変換 (4.11) を使用して常に正準形式 (4.10) に変換でき、位相平面上のその挙動を研究できます。ξ , η 。ここで考えられるさまざまなケースを考えてみましょう。

ルーツ λ 1 , λ 2 – 有効かつ同じ符号のもの

この場合、変換係数は実数であり、実平面から移動します。x、y実平面ξ、ηに。式 (4.10) の 2 番目を最初の式で割ると、次のようになります。:

.(4.12)

この方程式を積分すると、次のようになります。:

ここで .(4.13)

λ で理解することに同意しましょう 2 大きな係数を持つ特性方程式の根。これは推論の一般性に違反しません。次に、検討中のケースでは根 λ が 1 , λ2 – 有効かつ同じ符号のもの、ある>1 、放物線型の積分曲線を扱っています。

すべての積分曲線 (軸を除く) η に対応します。 ) 軸の原点にタッチします ξ, これは式 (4.11) の積分曲線でもあります。座標の原点は特別な点です。

ここで、位相軌跡に沿った代表点の移動方向を求めてみましょう。 λの場合 1、λ2 したがって、式 (4.10) からわかるように、|ξ|、|η| は負になります。時間の経過とともに減少します。代表点は座標原点に近づきますが、座標原点には到達しません。そうしないと、これは、位相平面の各点を通過する位相軌道は 1 つだけであるというコーシーの定理と矛盾することになります。

まるで放物線の集合のように、積分曲線が通過する特別な点原点を通過し、ノードと呼ばれます（図2）。 4.5)

λにおけるノードタイプの平衡状態 1、λ2 < 0 代表点がすべての積分曲線に沿って座標の原点に向かって移動するため、リアプノフは安定です。これ 安定した結び目。 λの場合 1、λ2 > 0、それでは |ξ|、|η| 時間の経過とともに増加し、代表点は座標の原点から遠ざかります。この場合の特別なポイントは、– 不安定なノード .

位相面上で x、y 積分曲線の挙動の一般的な定性的性質は保持されますが、積分曲線の接線は座標軸と一致しません。これらの接線の傾斜角は、係数の比率によって決まります。 α , β , γ , δ 式(4.11)において。

ルーツ λ 1 , λ 2 – は有効ですが、符号が異なります。

から変換座標 x、y 座標へ ξ, η またまたリアル。正規変数の方程式は再び (4.10) の形式になりますが、今度は λ の符号が変わります。 1、λ2 は異なります。位相軌跡の方程式は次の形式になります。:

ここで、(4.14)

(4.14) を積分すると、次のようになります。

(4.15)

これこの方程式は、双曲線タイプの曲線のファミリーを定義します。ここで、両方の座標軸は– 漸近線 ( ある=1 等辺双曲線の族ができます). この場合の座標軸も積分曲線です– これらは原点を通過する唯一の積分曲線になります。それぞれそのうちの 3 つのフェーズの軌道で構成されます: 平衡状態への (または平衡状態から) および平衡状態からの 2 つの動き。他のすべての積分曲線– 原点を通らない双曲線です(図1)。 4.6) この特別なポイントは次のように呼ばれます。 "サドル ». 山の鞍部付近のレベルラインは、鞍部付近の位相軌道と同様に動作します。

平衡状態に近い位相軌道に沿った代表点の移動の性質を考えてみましょう。たとえば、次のようにしましょう。λ 1 >0 、λ 2<0 。次に、軸上に配置された代表点 ξ 、原点から遠ざかり、軸上に配置されます η – 無限に座標の原点に近づきます, 限られた時間内に到達することなく. 初期瞬間における代表点の位置 (特異点と漸近線上の点を除く) η =0), 最初は積分曲線の 1 つに沿って特異点に向かって移動したとしても、最終的には平衡から遠ざかります。.

それは明らかです サドルのような特異点は常に不安定です . 漸近線における特別に選択された初期条件下でのみη =0 システムは平衡状態に近づきます。ただし、これはシステムの不安定性に関する声明と矛盾するものではありません。数えてみたら, 位相平面上のシステムのすべての初期状態が等しい確率である場合、その方向の動きに対応するそのような初期状態の確率に特異点はゼロに等しい。したがって、実際に動くとシステムは平衡状態から外れてしまいます。座標に戻りますx、y、座標の原点の周りの軌道の動きの性質について、同じ定性的な画像が得られます。

ノードとサドルの考慮されたケース間の境界は、次のとおりです。いつ特性指標の 1 つ、たとえば λ 1 , 消滅は、システムの決定要因が消滅したときに発生します。- 表現 ad-bc=0(式 4.8 を参照) ). この場合、式 (4.4) の右辺の係数は互いに比例します。:

そしてシステムはその平衡状態として線のすべての点を持っています:

残りの積分曲線は、角度係数を持つ一連の平行直線です。、それに沿って、特性方程式 λ の第 2 根の符号に応じて、代表点が平衡状態に近づくか平衡状態から遠ざかります。 2 = a+d。(図4.7 ) この場合、平衡状態の座標は変数の初期値に依存します。

ルーツ λ 1 , λ 2 – 複雑な共役

この場合、実際には×そして y私達はします複素共役を持つ ξ , η (4.10) . ただし、別の中間変換を導入することにより、この場合、考慮対象を実際の線形同次変換に減らすことも可能です。入れましょう:

(4.16)

どこ a、b、そして う、う – 実際の値。からの変換が示されることができます。x、yに う、う 私たちの仮定の下では、は実数で、線形で、ゼロとは異なる行列式で均一です。方程式により(4.10、4.16) 次のようになります。

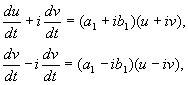
どこ

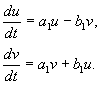(4.17)

方程式の 2 番目を最初の方程式で割ります。、次のようになります。

どちらが統合しやすいですか, 極座標系に行くと (り、 φ ) . 置換後どこから得ますか:

.(4.18)

したがって、位相平面上では、あなた、v私たちは対数螺旋の族を扱っています。それぞれの螺旋は次のようになります。原点における漸近点。特異点。スパイラルの形状を持つすべての積分曲線の漸近点です。, それぞれに入れ子になっている友達、それはそう呼ばれています集中 ( 図4.8 ) .

位相軌道に沿った代表点の移動の性質を考えてみましょう。方程式 (4.17) の最初の値に次の値を乗算します。あなた、2番目以降 vさらに追加すると、次のようになります。

どこ

させてある 1 < 0 (ある 1 = リλ ) 。そして、代表点は有限時間で座標原点に到達することなく、継続的に座標原点に近づいていく。これは、位相の軌跡がねじれた螺旋であり、減衰振動に対応していることを意味します。変数。これ - 安定した集中力 .

安定した焦点の場合、安定したノードの場合と同様に、リアプノフ条件が満たされるだけでなく、より厳しい要件も満たされます。つまり、初期の偏差については、時間の経過とともに、システムは希望どおり平衡位置に近い位置に戻ります。初期偏差が増加しないだけでなく、減衰してゼロに向かうこのような安定性を安定性と呼びます。 絶対的な安定性 .

式の場合 (4.18) ある 1 >0 、すると、代表点は原点から遠ざかり、次のようになります。 焦点が不安定 . 飛行機から移動する場合う、う位相面へ×, y螺旋も螺旋のままですが、変形します。

次に、次の場合を考えてみましょう。ある 1 =0 。平面上の位相軌跡あなた、vサークルもあるだろう飛行機の中ではどれx、y楕円に対応する:

したがって、いつ1=0 特別なポイントを通してx= 0、y= 0 積分曲線は通過しません。 このように積分曲線の近傍が閉曲線、特に楕円が埋め込まれて特異点を囲んでいる孤立した特異点を中心と呼ぶ。

したがって、特性方程式 (4.7) の根の性質に応じて、6 種類の平衡状態が可能です。平面上の位相軌跡の表示 x、yこれら 6 つのケースを図に示します。 4.9.

米。 4.9.連立一次方程式の定常状態付近の位相ポートレートの種類 (4.4)。

5 種類の平衡状態は大まかであり、方程式 (4.4) の右辺が十分に小さい変化ではその性質は変わりません。この場合、右辺の変化だけでなく、その一次導関数の変化も小さくなければなりません。バランスの 6 番目の状態である中心は、荒れていません。方程式の右側のパラメータを少し変えると、焦点が安定したり不安定になったりします。

分岐図

次の表記法を導入しましょう。

. (4.11)

この場合、特性方程式は次のように記述されます。

. (4.12)

直交するデカルト座標を持つ平面を考えます。 s , D そして、特性方程式の根の性質によって決定される、1 つまたは別のタイプの平衡状態に対応する領域をその上にマークします。

.(4.13)

平衡状態が安定する条件は、y の負の実部が存在することです。私 1と私 2 。そのための必要十分条件は、不等式が満たされることである。s > 0, D > 0 。図 (4.15) では、この条件はパラメータ平面の最初の 4 分の 1 に位置する点に対応します。特異点は次の場合に焦点になります。私 1と私 2 複雑な。この条件は、次のような平面上の点に対応します。 , それらの。放物線の 2 つの枝の間の点s 2 = 4 D。アクスルポイント s = 0, D>0、中心型の平衡状態に対応します。同じく、私 1と私 2 - は有効ですが、符号が異なります。つまり、特異点はサドルになります。 D<0, 等その結果、パラメータ平面の分割図が得られます。 s, D、さまざまなタイプの平衡状態に対応する領域に分割されます。

米。 4.10.分岐図

連立一次方程式の場合 4.4

線形システムの係数が a、b、c、d特定のパラメータに依存し、このパラメータが変更されると、値も変更されますs , D 。境界を越えると、位相ポートレートの性質は質的に変化します。したがって、このような境界は分岐境界と呼ばれます。境界の反対側では、システムにはトポロジー的に異なる 2 つの位相ポートレートがあり、それに応じて 2 つの異なるタイプの動作が示されます。

この図は、そのような変化がどのように発生するかを示しています。特殊なケース、つまり座標の原点を除外すると、縦軸を横切るときにサドルが安定または不安定なノードに変形する可能性があることが簡単にわかります。安定した結び目は、サドルに入る場合もあれば、安定した焦点に入る場合もあります。位相空間のトポロジーは変化しないため、安定ノード - 安定焦点および不安定ノード - 不安定焦点の遷移は分岐ではないことに注意してください。位相空間トポロジーと分岐遷移については、講義 6 で詳しく説明します。

分岐遷移中、特異点の安定性の性質が変化します。たとえば、中心を通る安定した焦点が不安定な焦点に変わる可能性があります。この分岐はと呼ばれます アンドロノフ・ホップ分岐それを研究した科学者の名前で。非線形システムのこの分岐中に、リミットサイクルが生まれ、システムは自己発振します (講義 8 を参照)。

例。線形化学反応システム

物質 ×外部から一定の速度で流れ込み、物質Yとなり、その濃度に比例した速度で変化する Y、反応範囲から削除されます。すべての反応は、ゼロ次の外部からの物質の流入を除いて、一次反応です。反応スキームは次のようになります。

(4.14)

そして、これは方程式系で記述されます。

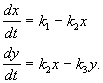(4.15)

右辺をゼロとみなすことで定常濃度を取得します。

.(4.16)

システムの位相ポートレートを考えてみましょう。システム (4.16) の 2 番目の方程式を最初の方程式で割ってみましょう。得られるものは次のとおりです。

.(4.17)

式 (4.17) は、位相平面上の変数の動作を決定します。このシステムの位相ポートレートを構築してみましょう。まず、位相平面上に主アイソクラインを描きましょう。垂直接線の等傾斜の方程式:

水平接線の等傾斜の方程式:

特異点 (定常状態) は、主等傾斜線の交点にあります。

次に、座標軸が積分曲線とどの角度で交差するかを決定しましょう。

もし x= 0、その後。

したがって、積分曲線の接線の接線は y=y(x)、縦軸と交差する x=0、上半平面では負です (変数が x、yは濃度値を持っているため、位相面の右上の象限のみに関心があります)。この場合、接線角度の正接は、原点から離れるにつれて増加します。

軸を考える y= 0. この軸が積分曲線と交差する点で、積分曲線は次の方程式で記述されます。

で横軸と交差する積分曲線の傾きの正接は正であり、増加するにつれてゼロから無限大まで増加します。 ×.

で。

その後、さらに増加すると、傾斜角の正接は絶対値で減少し、負の値のままで、次の時点で -1 になる傾向があります。 × ® ¥ 。主等傾斜面および座標軸上の積分曲線の接線の方向がわかれば、位相軌跡の全体像を構築するのが簡単になります。

Lyapunov 法を使用して、特異点の安定性の性質を確立してみましょう。システムの特性決定因子は次の形式になります。

行列式を展開すると、システムの特性方程式が得られます。、つまり特性方程式の根は両方とも負です。したがって、システムの定常状態は安定したノードです。この場合、物質の濃度は、 ×は常に単調に定常状態に向かう傾向があるため、物質 Y の濃度は最小値または最大値を通過する可能性があります。このようなシステムでは振動モードは不可能です。

意味。関数の特異点は次のように呼ばれます。 孤立した、 この点の近傍が解析関数 (つまり、リング内の解析関数) である場合。

関数の孤立した特異点の分類は、特異点の近傍におけるこの関数の動作に関連します。

意味。ポイントと呼ばれるものは、 取り外し可能な でこの関数の有限極限がある場合、関数の特異点。

例5。関数がある点に除去可能な特異点があることを示します。

解決。最初の顕著な限界を思い出して、計算します。

これは、ある時点で、指定された関数が削除可能な特異点を持つことを意味します。

タスク4。ポイントがに対して削除可能であることを示します。

意味。ポイントと呼ばれるものは、 ポール この関数がで無制限に増加する場合、つまり。

解析関数のゼロと極の概念間の関係に注目してみましょう。関数をの形式で表しましょう。

点が関数の単純なゼロである場合、その関数は単純な極を持ちます。

点が関数の次数のゼロである場合、その関数ではそれは極になります。 注文。

例6。この関数がある点に 3 次の極があることを示します。

解決。を取得すると仮定します。私たちはゼロにする傾向があるので、どの法律によってもです。そして、それに伴って関数自体も無限に増加します。したがって、、つまり特異点は極です。関数の場合、この点は明らかにトリプルゼロです。これは、この関数の点が 3 次の極であることを意味します。

タスク5。点に単純な極があることを示します。

意味。ポイントと呼ばれるものは、 かなり特別な この時点で関数の有限または無限の制限がない場合 (関数の動作が定義されていない場合)。

を関数の本質的に特異点としましょう。次に、任意の複素数に対して、に収束する一連の点があり、それに沿って値は次の傾向にあります。 ( ソホーツキーの定理）。

例7。ある点の関数に本質的な特徴があることを示します。

解決。点の近傍での指定された関数の動作を考えてみましょう。実軸の正の部分に沿っているとき (つまり)、とがあります。実軸の負の部分 (つまり) に沿っている場合、および。これは、に制限がないことを意味します。定義により、ある時点で関数には本質的な特異点があります。

ソホーツキーの定理の観点から、ゼロにおける関数の動作を考えてみましょう。ゼロと無限大以外の任意の複素数とします。

等式からを見つけます。と仮定すると、点のシーケンス、が得られます。明らかに、。この数列の各点で、関数はに等しいため、

タスク6。関数がある点に本質的な特異点があることを示します。

無限遠点は常に関数にとって特別なものとみなされます。。この関数が原点を中心とする特定の円の外側に他の特異点を持たない場合、その点は関数の孤立特異点と呼ばれます。

孤立特異点の分類はケースに拡張できます。

例8.この関数が無限遠に二重極を持つことを示します。

解決。関数を考えてみましょう。ここで、は点の近傍にある解析関数であり、およびです。これは、関数が無限遠に二重ゼロを持つことを意味しますが、その場合、関数の点は二重極になります。

例9。関数が無限遠に本質的な特異点を持つことを示します。

解決。同様の問題がプロジェクト 7 でも検討されています。無限遠点付近での関数の動作を考えてみましょう。実軸の正の部分に沿った場合と、実軸の負の部分に沿った場合。これは、ある点では関数に制限がなく、定義上、この点は本質的に特別であることを意味します。

ある点における関数の特異性の性質は、次のように判断できます。 主要部分 この付近でローラン展開。

定理1.ポイントとなるためには 取り外し可能な 関数の特異点の場合、対応するローラン展開が必要かつ十分です。 主要部分は含まれていませんでした。

タスク6。点の近傍で関数のテイラー展開を使用して、その関数がゼロに除去可能な特異点を持つことを示します。

定理2.ポイントとなるためには ポール 必要十分な機能なので、 主要部分 対応するローラン拡張 有限数のメンバーが含まれていた :

最大の負の項の数によって、極の次数が決まります。

この場合、関数は次のように表すことができます。

ここで、は点における解析関数、、は極の次数です。

例10。関数の点に単純な極があることを示します。

解決。その点を考えてみましょう。例 2 で得られた、この点の近傍でこの関数のローラン展開を使用してみましょう。

この展開の主要部分では、最大 (かつ唯一) の負の次数が 1 に等しいため、点はこの関数の単純な極になります。

この結果は別の方法で得られた可能性があります。それを次の形式で表して、と置きます。これは、との点で分析的な関数です。これは、(8) により、この時点でこの関数には単純な極があることを意味します。

別の方法: 点に単純なゼロを持つ関数を考えてみましょう。これは、この時点では単純な極があることを意味します。

同様に、関数をの形式で書くと、は点およびにおける解析関数であり、点が関数の単純な極であることがすぐにわかります。

タスク7。関数の点に 2 次の極があり、点に 4 次の極があることを示します。

定理3.ポイントとなるためには かなり特別な 機能の点では、それは必要かつ十分です 主要部分 ポイント付近でのローランの展開 無限の数のメンバーが含まれていた .

例11.関数のある点における特異点の性質を決定する

解決。よく知られているコサイン展開では、次の代わりに次のようにします。

これは、点の近傍におけるローラン展開が次の形式を持つことを意味します。

ここで正しい部分は 1 つの項です。そして、メイン部分には無限の数の用語が含まれているため、その点は本質的に特別です。

タスク8。ある点で関数が本質的な特異点を持つことを示します。

いくつかの関数を考えて、その時点でのローラン展開を書いてみましょう。

置き換えてみましょう。本題に入ります。さて、無限遠点の近くでは、次のようになります。

新しい呼称の導入はまだ残っている。得ます

ここで、は主要部分であり、は無限遠点付近の関数のローラン展開の正しい部分です。したがって、点の近傍における関数のローラン展開では、主要部分は正の累乗の系列であり、正しい部分は負の累乗の系列になります。これを考慮して交換します

ただし、特異点の性質を判断するための上記の基準は、無限遠点についても有効です。

例12。その点における関数の特異点の性質を調べます。、その場合、ポイントは孤立していないことが判明する可能性があります。

例15。無限遠点における関数には本質的な特徴があります。関数の点が孤立特異点ではないことを示します。

解決。この関数は、分母のゼロ点、つまり点、に無限の数の極を持ちます。以来、極が存在する近傍の点が極の限界となります。

テイラー級数は、円 zol で解析的な関数を研究するための効果的なツールとして機能します。環領域で解析的な関数を研究するには、次の形式の正および負の累乗 (z - zq) での展開を構築できることがわかります。これはテイラー展開を一般化します。系列 (1) は 2 つの系列の合計として理解され、ローラン系列と呼ばれます。系列 (1) の収束領域が、系列 (2) のそれぞれの収束領域の共通部分であることは明らかです。彼女を探しましょう。最初の系列の収束領域は、コーシーアダマールの公式によって半径が決定される円です。収束円の内側では、系列 (3) は解析関数に収束し、より小さい半径の円では収束します。絶対的かつ均一に。 2 番目の系列は、変数に関するべき級数です。系列 (5) は、その収束円内で複素変数 m-*oo の解析関数に収束し、より小さな半径の円内では絶対的かつ一様に収束します。系列 (4) の収束領域が円の外側であることを意味します - 系列 (3) と (4) の共通の収束領域がある場合 - 系列 (1) が含まれる円環解析関数に収束します。また、どのリングにおいても絶対的に一様に収束する。例 1. rad ローラン級数の収束領域を決定する孤立特異点とその分類 M 最初の系列の収束領域は円の外側であり、2 番目の系列の収束領域は円の内側です。したがって、次のようになります。この級数は円に収束する定理 15. 円環内で明確かつ非政治的な関数 f (z) は、この環内で収束級数の和として表すことができ、その係数 Cn は次の式に従って一意に決定され計算されます。ここで、7p は半径 m の円です。リング R 内の任意の点 z を固定します。点 r を中心とし、その半径が不等式を満たす円を構築し、乗算結合領域に対するコーシーの積分定理を使用して、和の各積分を個別に変換します (8)。円 7d* に沿ったすべての点 £ について、一様収束級数 1 1 の desum 関係が満たされます。したがって、分数 ^ は、両方の部分に連続関数 (O を乗じて実行することによって) で表すことができます。円に沿って項ごとに積分すると、円上のすべての点 £ について、わずかに異なる方法で 2 番目の積分の変換を実行することがわかります。したがって、分数 ^ を表すことができます。両方の部分に連続関数を掛けて、円 7/ に沿って項積分すると、式 (10) と (12) の被積分関数は円環内の解析関数であることに注意してください。したがって、コーシーの定理により、円 7/r と 7r/ を任意の円に置き換えても、対応する積分の値は変わりません。これにより、式 (10) と式 (12) を組み合わせることができ、式 (8) の右側の積分をそれぞれ式 (9) と式 (11) に置き換えることで、z が任意であるため、必要な展開を得ることができます。リングの点では、級数 (14) はこのリングのどこでも関数 f(z) に収束し、どのリングでも級数は絶対的かつ一様にこの関数に収束します。ここで、形式 (6) の分解が一意であることを証明しましょう。もう 1 つの展開があると仮定します。そのとき、円周上では、級数 (15) が均一に収束します。等式の両辺を掛けてみましょう (m は固定の整数で、両方の級数を項ごとに積分します。その結果、左側では St が得られ、右側では St が得られます。したがって、(4, = St. m は任意の数で、最後の等式は展開の一意性を証明します。その係数は式 (7) を使用して計算され、リング内の関数 f(z) のローラン級数と呼ばれます。非負の累乗を持つこの級数の項のセットはローラン級数の正しい部分と呼ばれ、負の累乗を持つ項のセットはローラン級数の主要部分と呼ばれます。ローラン級数の係数の式 (.7) は実際にはほとんど使用されません。通常は、可能であれば、基本関数の既製のテイラー展開が使用されます。どの正当な方法でも、ローラン級数での展開を考えてみましょう。 f(r) に 2 つの特異点があると仮定して、さまざまな領域の関数の分布を計算します。したがって、点 r = 0 を中心とする 3 つのリング領域が存在します。それぞれの領域で、関数 /(r) は解析的です。 ) 円リング円の外側 (図 27)。これらの各領域で関数 /(z) のローラン展開を見つけてみましょう。 /(z) を素分数の和で表すとします。 a) 円関係式 (16) を等比級数の項の和の公式を使って次のように変形し、式 (17) に代入します。 : この展開は関数 /(z) のテイラー級数です。 b) |z| に対する関数 j^j の系列 (19) のため、関数 -r のリングはこのリング内で収束したままになります。 > 1 は発散します。したがって、関数 /(z) を次のように変形します。式 (19) を再び適用すると、この級数が収束することがわかります。展開 (18) と (21) を関係 (20) に代入すると、c) |z| の関数 -z の円の外側が得られます。 > 2 は発散し、関数の級数 (21) - 関数 /(z) を次の形式で表しましょう。<*>式 (18) と (19) を使用すると、OR 1 が得られます。この例は、同じ関数 f(z) に対して、ローラン展開は、一般に、異なる環に対して異なる形式を持つことを示しています。例 3. 関数ローラン級数の 8 番目のローラン級数の展開を求めます。リング領域での孤立特異点とその分類 A 関数 f(z) の表現を次の形式で使用します。等比数列の項の和を求める式が得られます。見つかった式を式 (22) に代入すると、例 4 が得られます。 zq = 0 の点でローラン級数の関数を展開します。任意の複素数について、これを置きます。展開は任意の点 z Ф 0 に対して有効です。この場合環状領域は、z - 0 の 1 つの捨てられた点を持つ複素平面全体を表します。この領域は、次の関係によって定義できます。この関数は、次の領域で解析的です。ローラン級数の係数の式 (13) から、同じものを使用します。前の段落と同様に推論すると、不等式 Kouiw が得られます。関数 f(z) が円上で境界がある場合 (M は定数)、孤立特異点点 zo の環近傍がある場合、点 zo は関数 f(z) の孤立特異点と呼ばれます (このセットは、点 2o) のパンクチャド近傍と呼ばれることもあり、関数 f(z) は一意で分析的です。 zo 自体の点では、関数は未定義であるか、明確で分析的ではありません。点 zo に近づくときの関数 /(r) の動作に応じて、3 種類の特異点が区別されます。孤立特異点は次のように言われます: 1) 有限が存在する場合は除去可能 2) 有限である場合は pmusach 3) 関数 f(z) に制限がない場合は本質的に特異点孤立特異点のタイプは、の穴の開いた中心による関数のローラン展開の性質。定理 16. 関数 f(z) の孤立特異点 z0 は、点 zo の近傍における関数 f(z) のローラン展開が主部分を含まない場合に限り、除去可能な特異点です。の形は zo を取り外し可能な特異点とします。したがって、関数 f(z) は点 z のプロコロジー近傍で制限されます。コーシーの不等式によって、p は任意に小さく選択できるため、すべての係数は負のべき乗 (z - 20) はゼロに等しい: 逆に、点 zq の近傍における関数 /(r) のローラン展開には正しい部分のみが含まれているとします。つまり、それは (23) の形式を持ち、したがって次のようになります。テイラー。 z -* z0 の場合、関数 /(z) には限界値があることが簡単に分かります: 定理 17。関数 f(z) の孤立特異点 zq は、関数 J(z) が次の場合に限り除去可能です。点 zq の穴が開いた近傍で境界が定められていますが、Zgmechai は境界を定めていません。 r を関数 /(r) の除去可能な特異点とする。関数 /(r) が点 r を中心とする円内で解析的であると仮定します。これにより、ポイントの名前 (取り外し可能) が決まります。 e. は次の形式になります。 4 z0 を極とします。それ以来、関数 f(z) が解析的で非ゼロである点 z0 のパンクチャされた近傍が存在します。次に、この近傍で解析関数が定義されます。したがって、点 zq は関数の除去可能な特異点 (ゼロ)、または h(z) が解析関数 h(z0) Φ 0 です。その場合、h(zo) Φ 0 も解析的である場合、関数 φ は点 zq の近傍で解析的であるため、どこからそれを取得するか、関数 f(z) が次のパンクチャされた近傍で (24) の形式の展開を持つと仮定します。ポイントz®。これは、この近傍では関数 f(z) が関数とともに解析的であることを意味します。関数 g(z) の展開は有効であり、そこから zq が関数 g(z) の除去可能な特異点であり、存在することがわかります。その場合、0 にある関数が関数の極となる傾向があります。これも単純な事実です。点 Zq は、関数 g(z) = yj を g(z0) = 0 と設定して点 zq の近傍の解析関数に拡張できる場合に限り、関数 f(z) の極になります。関数 f(z) の極の 0 次は関数 jfa のゼロ次と呼ばれます。次のステートメントは定理 16 と 18 から導かれます。定理 19. 孤立特異点は、この点のパンクされた近傍におけるローラン展開の主部分に無限に多くの非ゼロ項が含まれる場合に限り、本質的に特異です。例 5. 関数の特異点は zo = 0 です。ローラン級数の孤立特異点とその分類があります。したがって、zo = O は除去可能な特異点です。関数 /(z) をゼロ点付近のローラン級数に展開すると、正しい部分のみが含まれます: 例 7。 /(z) = 関数 f(z) の特異点は zq = 0 です。実軸と虚軸でこの関数の動作を考えてみましょう。実軸では x 0、虚軸では次のようになります。は、z -* 0 における f(z) の有限または無限の極限ではありません。これは、点 r = 0 が関数 f(z) の本質的に特異点であることを意味します。関数 f(z) のゼロ点付近でのローラン展開を求めてみましょう。任意の複素数 C に対して Set があります。次に、ローラン展開には、z の負の累乗を持つ項が無限に含まれます。

基本的な概念と定義:

解析関数 f(z) のゼロは、f(a)=0 となる点「a」です。

関数 f(z) の次数「n」のゼロは、fn(a)¹0 であれば点「a」になります。

特異点ａの近傍にａ以外に特異点が存在しない場合、関数ｆ（ｚ）の孤立特異点と呼ばれる。

孤立特異点には 3 つのタイプがあります。

取り外し可能な特異点 1 つ;

3 つの本質的に特異点。

特異点の種類は、見つかった特異点における特定の関数の挙動に基づいて、また、見つかった特異点の近傍の関数に対して取得されたローラン級数の形式から決定できます。

特異点における関数の動作によって特異点のタイプを決定します。

1. 除去可能な特異点.

有限極限がある場合、関数 f(z) の孤立特異点 a は除去可能と呼ばれます。

2.極。

関数 f(z) の孤立特異点 a を極と呼びます。 .

3. 本質的に特異点。

関数 f(z) の孤立特異点 a は、有限も無限も存在しない場合、本質的特異点と呼ばれます。

関数の零点と極の間には次の関係が存在します。

点 a が関数 f(Z) の次数 n の極であるためには、この点が関数の次数 n の零点であることが必要かつ十分です。

n=1 の場合、その極は単純と呼ばれます。

意味：明確な性質を持つ孤立した特異点は次のように呼ばれます。

a) 分解の主要部分が欠落している場合は除去可能。

b) 主要部分に有限数の項が含まれる場合は極。

c) メイン部分に無限の数の項が含まれる場合、本質的に特異点。

a) したがって、除去可能な特異点の近傍では、展開は次の形式になります。

それは円 |z-a| のすべての点における関数を表します。

中心 z=a では等式は真ではありません。 z=a の関数には不連続性があり、右側は連続です。中央の関数の値が変更され、それが右側の値と等しくなる場合、ギャップは解消されます。したがって、名前は削除可能です。

b) m 次の極の近傍では、ローラン級数展開は次の形式になります。

c) 簡易ポールの付近

控除とその計算式。

孤立特異点 z 0 における解析関数 f(z) の剰余は、積分の値に等しい複素数です。、関数 f(z) の解析領域内 (つまりリング 0 内) にある点 z 0 を中心とする円 L に沿って正の方向に取られます。<|z-z0|

孤立特異点 z 0 における関数 f(z) の剰余は、記号 Res f(z 0) または Res (f(z); z 0) で表されます。したがって、

解像度 f(z 0)= . (22.15.1)

式 (22.15.1) に n=-1 を入れると、次のようになります。

C -1 =

または Res f(z 0)= C -1 、

それらの。特異点 z 0 に関する関数 f(z) の剰余は、ローラン級数における関数 f(z) の展開における負の指数を持つ最初の項の係数に等しい。

控除額の計算。

通常の特異点または取り外し可能な特異点。明らかに、z=z 0 が関数 f(z) の正則特異点または除去可能な特異点である場合、Res f(z 0)=0 (これらの場合のローラン展開には主要部分が欠けているため、c-1=0) になります。。

ポール。点 z 0 を関数 f(z) の単純な極とする。このとき、点 z 0 の近傍における関数 f(z) のローラン級数は次の形式になります。

ここから

したがって、この等式を z --z 0 の極限まで渡すと、次のようになります。

解像度 f(z0)=

基本的に特別なポイント。点 z 0 が関数 f(z) の本質的に特異点である場合、この点での関数の剰余を計算するには、通常、関数のローラン級数展開の係数 c-1 が直接決定されます。

イベントの分類。イベントの和、積、そのプロパティ、グラフィック表現。

イベントは次のように分類されます。

1.ランダム

2. 信頼できる

3. 不可能

信頼できるとは、与えられた条件下 (朝の後に夜) で必ず発生するイベントです。

ランダムイベントとは、起こるかもしれないし、起こらないかもしれない（試験に合格する）イベントです。

不可能な出来事とは、与えられた条件下（赤鉛筆しか入っていない箱から緑鉛筆を取り出すなど）では起こらない出来事です。

させて zq は関数 /(r) の特異点、t.s. f(z)ただし、この時点では分析的です (特に、この時点では定義されていない可能性があります)。ポイント付近にこのような穴が開いている場合 zq (つまり、集合 O z - zq f(z) はアイアライト語です。ぞ呼ばれた 孤立特異点機能 f(z)。この定義は次の場合も変わりません。 zn =おお、ポイント付近にヨウ素が刺さってしまったら zq = oo 理解集合 z>私 - 原点を中心とする円の外側。つまり特別なポイント zq は、この点の近傍に、この点以外の他の特異点が存在する場合に孤立していると言われます。 zq. 以下の説明では、一意の特性 (関数) の特異点のみを考慮します。 f(z)明確であると想定されます）。

関数の動作に応じて f(z)で z -> zq特異点には 3 種類あります。孤立特異点 zq 関数 f(z)呼ばれます:

1) 取り外し可能な特異点、有限の制限がある場合

2) ポール、制限がある場合

3) 基本的に特別なポイントですが、もし f(z) には有限制限も無限制限もありません。 z-> zq.

例26.1。 3 種類の特異点がすべて実現されることを示しましょう。考えてみましょう f(z)= ポイント zq = 0 は孤立します

この機能の特別なポイント。式 (22.12) を使用すると、次の展開が得られます。

そこから、lim が存在することがわかります。 fi(z)= 1。したがって、zq = 0 は

関数の取り外し可能な特異点です fi(z)。

関数 f‘j(z) =---点にポールがありますぞ= 1 なぜなら

2 r「×」

では関数を考えてみましょう )з(z)= e 1 ^ r そしてそれを示しますゾ＝ O は、この関数の本質的に特異点です。努力するとき z実軸に沿ってゼロに、関数 /z の左端と右端をゼロにします。 (z)違う：リムと 1 / 1 = 0、リム s 1 /* =オス。このことから、

x->0-0 x->0+O

何 f:i(z) 2 には有限または無限の制限がありません -> ああ、そうです。 zq = O は、この関数の本質的に特異点です。 (ポイントは傾向があるので注意してください) z - iy虚軸関数に沿ってゼロに

制限はまったくありません。)

もちろん、孤立していない特異点も存在します。例えば。関数には点に極があります zn = -, n= ±1、±2、...

したがって、 Zq = 0 は、この関数の孤立していない特異点です。この点の近傍には (どんなに小さくても) 他の特異点が存在します。 g p.

させてぞー関数の有限の孤立特異点 f(z)。それから f(z) 0 Zo ポイントのいくつかの穴が開いた近傍では同様ですぞこの近傍は、内半径 r = 0 のリングと考えることができます。定理 25.1 により、考慮中の近傍では次の関数が得られます。 f(z)ローラン級数 (25.2) に拡張できます。 2 での関数の動作を示します。 -> zq (つまり、特異点のタイプ) ぞ）拡張の主要部分のタイプに依存します (25.2)。この状況が「主要部分」という用語の由来を説明しています。

定理 2G.2。 関数 f(z) の孤立特異点 zo は、この点のパンクされた近傍の Lorap 展開が oid を持っている場合に限り、削除可能です。

それらの。正しい部分だけで構成されている, 主要部分のすべての係数は黒丸と等しくなります。

証拠。 1. しましょうぞ- 取り外し可能な特異点。関数のローラン展開が成り立つことを証明しましょう。 f(z)の形式は (26.1) です。スペシャルポイントなのでぞ取り外し可能である場合、制限には限界があります f(z) = A.したがって、 f(z) 0 z - zq 点のパンクされた近傍で境界が定められていますぞ、それらの。 )(z) みんなのために zこの付近から。どれでも取りましょう r. U р /?| を計算し、ローラン級数の係数には式 (25.3) を使用します。

展開主要部の係数について n =- 1、-2、... このような値の場合 n我々は持っています p〜p-e 0 で r-> 0.値なので r任意に小さい値を選択できます。 さん～」必要に応じて小さくすることができます。 |s t 以来、| ^ さん～ｐそして、c は p に依存しないため、次の時点で c `` = 0 そして= - 1、-2、...、これは証明する必要があるものです。

2. ここで、ローラン展開が (26.1) の形式を持つと仮定します。級数 (26.1) はべき級数です。したがって、穿刺された領域だけでなく、その周囲全体にも収束します。 z-zq その点も含めてぞ、その量 S(z)で分析しています z と S(z) = )(z) 0zで - ぞ R.したがって、有限の制限limがあります )(z)= Pt 5(g) = 5(th) - したがって、特異点 zq

Z->Zo Z-*Zo

取り外し可能。定理は証明されました。

コメント。定理の証明から、除去可能な特異点のパンクチャされた近傍 0 z - zo では、次の関数が得られます。 f(z)近傍全体で解析的な関数 5(r) と一致します。 z - ゾ。したがって、/(th) = と設定すると、 S(zq)、その後、関数の値を変更せずに f(z)パンクチャされた近傍の任意の点で、この関数を Go で分析的にします。その機能を「削除」しましょう。これは「取り外し可能な機能」という用語の説明です。このような点は関数の特異点ではなく規則的なものであると考えるのが自然です。 f(z)。

たとえば、次の関数を考えてみましょう。

例 26.1 では、Pm Nr) = 1 であることが示されました。特異点

zq = 0 は取り外し可能です。 /i(0) = 1 に設定すると、特異点が除去され、その点で解析的な関数が得られます。 zq = 0 (および C プレーン全体)。

ここで、ローラン展開の観点から極を特徴づけてみましょう。

定理26.3。 関数 f(z) の孤立特異点 Zo は、次の場合にのみ極になります。, Zq を中心とするローラン展開の主要部分に有限数の異なる要素しかない場合

n のゼロ係数から:

証拠。 1. しましょう zq - 極、つまりリム/( z) = ああ。

関数のローラン展開が成り立つことを証明しましょう。 f(z)形式は (2G.2) です。リム以来 f(z)= ああ。ポイントの付近に穴が開いています

キ zq. どの中で f(z)は分析的であり、ゼロはありません。それから関数 g(z) = 1 /f(z)このパンクした近傍でも分析され、リムは g(z)= 0。したがって、ゾ取り外し可能です *-? *0

関数の特異点 g(z)。定義しましょう g(z)時点でぞ、置く グ（ゾ）= 0.それでは g(z)(貫通されていない) ポイントの近傍全体が解析的になります z 0 、そして z0孤立したゼロになります。で表しましょう Nこのゼロの多重度 (次数)。 §23で示したように、点の近傍では zq関数 g(z)の形式で表すことができます ((23.2) を参照)

そして (z$) f 0と y>(z)ポイントの近傍で分析的であるぞーなぜなら ip(z)ある点で連続するぞそして g>(ゾ)Ф 0"では ip(z)この点の近傍にはゼロがありません。したがって、関数 1 /-p(z)はこの近傍でも解析的であるため、テイラー級数で展開されます。

括弧を開いて係数の指定を変更し、最後の展開を次の形式で記述します。

ここで、c_jv = 1>of 0. したがって、関数 /(r) のローラン展開の主要部分には、有限数の項のみが含まれます。望ましい等価性 (26.2) に到達しました。

2. 点の穴が開いた付近を入力します。番目関数 )(z)はローラン展開 (26.2) (より詳細な形式については (26.3) を参照) で表され、その主要部分には有限数の項のみが含まれます。と-で」 f 0. を証明する必要がある Zq - 関数極 f(z)。等式 (26.3) の乗算 (G - G o) iV 、関数を取得します

(26.4) の級数は、穿刺された点だけでなく、点の近傍全体でも解析関数に収束するべき級数です。 Zq. したがって、関数は h(z) go でさらに定義すると、この辺が分析的になります。 ひ（ぞ）= s_dg f 0.それでは

したがって、点 th は極であり、定理 26.3 が証明されます。

ゼロ関数の多重度（次数） g(z)= 1//(r) が呼び出されます 極の順序番目の関数は /(r) です。もし N- th の極の順序、その後 g(z)= (g - ゾ）ニップ（ズ）、そして（行きます） F 0、そして、定理 26.3 の証明の最初の部分に示されているように、関数 /(r) の展開は (26.3) の形式になります。ここで、c_/v f 0. 逆に、/(r) を級数 (26.3) に展開すると、 え～いF 0、それでは

t.s. N-関数 /(r) の極の次数。したがって、 zq 関数の極次数/(G) 点 zq のパンクチャされた近傍におけるローラン展開の主要部分の最大の非ゼロ係数の数に等しい(つまり、この数値と等しいん、何のs_dg f 0とスプ= 0時 n > N）。

アプリケーションに便利な次のステートメントを証明しましょう。

結果 26.4。 点 zq はフィクションの次数 N の極です/(G) そのとき、そのときだけ/(G) 形で表現できる

ここで、h(z) は点付近の解析関数です。番目 そしてh(zo)f 0.

証拠。関数 cp(z) = l/h(z)は点 h の近傍で解析的です。系 26.4 の条件は次と同等です。

それが理由です zq - 多重度ゼロ N機能 g(z)。したがって多重性の極 N関数 /(2)。

II 例 26.5。関数の孤立特異点を見つけるそしてそのタイプを判断します。

解決策: ポイントは次のとおりです。 (z 2 + 1 )(z+ Z) 2 = 0。 z 2 L- 1 = 0、その後 2 = ±gもし (z 4-3) 2 = 0 の場合 z= -3。したがって、この関数には 3 つの特異点があります。 z= g、22 = -g、 Z3 = - 3. 検討する z:

G -一次極 (系 26.4 を使用しました)。 22 = と同様の方法で証明できます。 -私一次の極でもあります。 2z の場合は次のようになります。

本質的に特異点について考えてみましょう。

定理26.6。関数 f(z) の孤立特異点 zq は、zq を中心とするローラン展開の主部分に無限に多くの異なる点がある場合に限り、本質的に特異点となります。ゼロ、p からの係数。

証拠。定理 26.6 は、定理 26.2 および 26.3 から直接続きます。確かに、その点であれば、 zq は本質的に特殊であるため、ローラン展開の主要部分が存在しなかったり、有限数の項が含まれたりすることはできません (そうでない場合は、 Zqは取り外し可能かポールになります）。したがって、主要部分の項の数は無限でなければなりません。

逆に、メイン部分に無限に多くの用語が含まれている場合、 Zq は、取り外し可能なポイントでもポールでもありません。したがって、この点は本質的に特別であるということになります。

定義によれば、本質的に特異点は、関数 /(2) が次の点に対して有限または無限の制限を持たないという事実によって特徴付けられます。 z ->zq. 本質的に特異点の近傍で関数の動作がどの程度不規則であるかについてのより完全なアイデアは、次の定理によって与えられます。

定理 26.7 (ソホーツキーの定理)。 zq が人にとって必須である場合、関数 f(z), 次に、任意の複素数に対して L、 Aを含む =おお、 z n -> zo となる一連の点 z n があり、リム f(zn) = A.

n->os

証拠。まずケースを考えてみましょう A =ああ。定理 2G.2 の証明の最初の部分で、次のことが証明されました。 f(z)点 r のパンクチャされた近傍で境界があり、すべての係数 c"、 n = -主要部分の 1,- 2,... はゼロに等しい (したがって、go の特異点は除去可能である)。条件により th は本質的な特異点であるため、点 th のパンクチャされた近傍では関数 f(r) は無制限になります。次のような強力な近傍 0 Z を考えてみましょう。 f(zi) > 1 (|/(r)| z - zo I/2 の場合、点があります z-2 、ここで |/(yy)| > 2 など: 穴が開いた付近 O 71. rn -e go および lim /(r“) = oo であることは明らかです。したがって、A = oo の場合、定理 26.7

証明された。

今すぐしましょう Afああ。まず、パンクした近傍 0 があると仮定します。

= -yy---- このパンクした近傍では分析的になるため、その結果、

/(G) - あ

したがって、 go は関数 Φ(r) の孤立特異点になります。ご紹介します。 r は Φ(r) の本質的に特異点です。これは真実ではないかもしれません。その場合、有限または無限の限界 lim Ф(r) が存在します。しばらくの間

/(r) = A + の場合、条件に矛盾する Hsh /(r) もあります。

F(g) ~ :-*z0

定理が分かりました。したがって、r0 は関数 Φ(r) の本質的に特異点です。上で証明されたことによると、r n 番目と lim Ф(r n) = oo となる一連の点 r n が存在します。ここから

/(r) という仮定の下で必要なステートメントを証明しました。 FA点 go のいくつかの穴が開いた近傍で - ここで、これが誤りであると仮定しましょう。点の任意に小さな穴が開いた近傍には、そのような点が存在します。 ぐ」、/(r") = L であること。そして、任意の場合 nパンクチャされた近傍 0 f(z u) = А では、目的のステートメントは true になります。 n-ユオ

すべての場合において定理 26.7 が証明されます。

定理 26.7 (ソホーツキー) によると、本質的に特異な点の任意の (任意に小さい) パンクチャリングされた近傍において、関数 /(r) は拡張複素平面 C から任意の数に近い値を取得します。

孤立特異点を研究するには、基本的な初等関数の既知のテイラー展開が役立つことがよくあります。

例2G.8。関数の特異点 zq = 0 のタイプを決定します。

解いて e. (22.11) に代入して、分子と分母をテイラー級数に展開します。 z r から 1 を引く代わりに、次のようになります。

(22.12) を使用して、分母の展開を取得します。

これらの展開の級数は、複素平面 € 全体に収束します。我々は持っています

および /2(2) は点の近傍でアナリティックですゾ＝ 0 (平面全体でも) および /2(20) F 0、それでは h(z)点 gF 0 の近傍でも解析的です。系 26.4 によれば、点はゾ＝ 0 は順序の極です N=4。

II 例 26.9。関数の特異点を見つける f(z)= sin j - そしてそれらのタイプを決定します。

Re in e i e 関数には単一の有限特異点があります。 zq = 1。C の他の点では、関数 w =--- 分析的。したがって関数 sin w分析的になります。

r の代わりに - を正弦 (22.12) の展開に代入すると、次のようになります。

点 2o = 1 の穴が開いた近傍における関数 sin のローラン級数への展開が得られました。結果として得られる展開には、負の累乗 (r - 1) を持つ項が無限に多く含まれるため、次のようになります。 zq = 1 は本質的に特異点です (この場合、ローラン展開は主部分のみで構成され、正規部分が欠落しています)。

この場合、級数展開に頼ることなく、定義から直接特異点の性質を確立することが可能であることに注意してください。実際、次のように収束するシーケンス (r",) と (2") があります。ぞ= 1 など f(z"n)= 1、/(2") = 0 (そのようなシーケンスは自分で指定してください)。 f(z)に制限はありません z -> 1 したがってポイント zq-1 は本質的に特別です。

点の近傍における関数のローラン展開の概念を導入しましょう Zq = 00 とし、この時点での拡張と特異点の性質との関係を考えます。孤立特異点の定義とそのタイプ (除去可能、極、または本質的に特異点) がこのケースに引き継がれることに注意してください。変更なしの zq = oc。ただし、定理 26.2。ローラン拡張の性質に関連する 26.3 と 26.6 は変更する必要があります。ポイントはメンバーです cn(z- 2o) p. n= -1,-2,..., メイン部分、終点付近の関数の「不規則性」を定義 Zq、2 は oo の傾向があるため、「正しく」動作します (0 の傾向)。逆に、正しいパートのメンバーは、 n= 1,2,... は oo になる傾向があります。それらは機能の性質を決定します Zq = ああ。したがって、oo 付近の展開の主要部分は正のべき乗をもつ項で構成されます。ぷ、そして正しいもの - 否定的なもの。

新しい変数を導入しましょう w = 1/2。関数 テレビ = 1/2、u(oo) = 0 になるように拡張され、近傍を 1 対 1 で等角にマッピングします。 z > Rポイント |w| 付近では zq = 00 wq = 0。関数の場合 f(z)パンクした地域の分析 R z Zq = oc、その後関数 G(w) = f(l/w)グレート近傍 0 wo = 0 で解析的になります。 2 -> oo では次のようになります。 w-> 0、その後

それが理由です G(w)要点にある wq = 0 は、と同じタイプの機能です。 f(z)時点で Zq = 00。関数 G(w) を、点 wo = 0 の穴が開いた近傍のローラン級数に拡張してみましょう。

(26.5) の右側の合計は、それぞれ展開の正規部分と主部分を表します。変数に移りましょう z、置き換える w = 1/z:

指定する n= -A*、6* = 6_`` = スパそしてそれに気づいて G(l/z) = f(z）、取得します

分解 (2G.G) は次のように呼ばれます。 点 zq のパンクチャされた近傍における関数 f(z) のローラン展開= ああ。 (2G.6) の最初の合計は次のように呼ばれます。 右側の部分、2番目の合計は 主要部分この分解の様子。これらの合計は展開 (26.5) の正しい主部分に対応するため、定理 26.2、26.3、および 26.6 の類似物は展開 (26.6) に有効です。したがって、次の定理は定理 26.2 に類似したものになります。

定理26.10。 孤立特異点Zq - OS (関数/(G) この点の穴が開いた近傍のローラン展開が次の形式を持つ場合に限り、削除可能です。

t.s. 正しい部分のみで構成されています。

/(oo) = と入れてみましょう 共同。近傍で収束する級数 (26.7) によって定義される関数 z > R点 2o = oc、と呼ばれます 点zでの解析的オー＝オー。 (この定義は関数の分析性と同等であることに注意してください) G(w) 時点でを = 0.)

例26.11。関数の特異点 zq = oo を調べる

限界は有限なので、ゾ＝ oo は関数 /(r) の除去可能な特異点です。 /(oo) = lim とすると J(z)= 0 の場合 f(z)分析的になるだろう

その時点でチックゾ= オス。対応する展開 (26.7) を見つける方法を示しましょう。変数に移りましょう w = 1 fz.置き換える z= 1 /?е、得られます

(最後の等式は点 w® = 0 のパンクチャされた近傍で有効ですが、(7(0) = 0) をさらに定義します。結果の関数には特異点があります。 w =±i、 w =-1/3、そしてその時点で Wq = 0 は解析的です。展開機能 G(w)徐々に w(例 25.7 で行ったように) 結果のべき級数に代入します。 w = 1/z、関数の拡張 (26.7) を得ることができます。 f(z)。

この場合の定理 26.3 ぞ= oo は以下の形に書き換えられます。

定理26.12 孤立特異点 th = os 関数 f(z) は、ローラン展開の主部分である場合にのみ極になります。 (26.6) 有限数の非ゼロ係数のみを持つと"：

ここで、級数は通常の部分であり、括弧内の多項式が展開の主要部分です。 oc の極多重度は、極多重度として定義されます。 wq = 0 関数 G(z)。極の多重度が数と一致していることが簡単にわかります。 N(26.8)で。

Qp | (i 2 + 1)(z+3) 2

タスク。関数があることを示す f(z) =-- -- が入っています

ポイントゾ＝オーダー 3 の oo ポール。

本質的に特異点に関する定理 26.6 は、次の場合に書き換えることができます。ぞ= os はほぼそのままなので、これについては詳しく説明しません。