What is a derivative?

Derivative table.

The derivative is one of the main concepts of higher mathematics. In this lesson, we will introduce this concept. Let's get acquainted, without strict mathematical formulations and proofs.

This introduction will allow you to:

Understand the essence of simple tasks with a derivative;

Successfully solve these very simple tasks;

Prepare for more serious derivative lessons.

First, a pleasant surprise.

The strict definition of the derivative is based on the theory of limits, and the thing is rather complicated. It's upsetting. But the practical application of the derivative, as a rule, does not require such extensive and deep knowledge!

To successfully complete most tasks at school and university, it is enough to know just a few terms- to understand the task, and just a few rules- to solve it. And that's it. This makes me happy.

Shall we get to know each other?)

Terms and designations.

There are many mathematical operations in elementary mathematics. Addition, subtraction, multiplication, exponentiation, logarithm, etc. If one more operation is added to these operations, elementary mathematics becomes higher. This new operation is called differentiation. The definition and meaning of this operation will be discussed in separate lessons.

Here it is important to understand that differentiation is just a mathematical operation on a function. We take any function and, according to certain rules, transform it. The result will be new feature. This new function is called: derivative.

Differentiation- action on a function.

Derivative is the result of this action.

Just like, for example, sum is the result of the addition. Or private is the result of the division.

Knowing the terms, you can at least understand the tasks.) The wording is as follows: find the derivative of a function; take the derivative; differentiate the function; calculate derivative etc. It's all same. Of course, there are more complex tasks, where finding the derivative (differentiation) will be just one of the steps in solving the task.

The derivative is denoted by a dash at the top right above the function. Like this: y" or f"(x) or S"(t) and so on.

read y stroke, ef stroke from x, es stroke from te, well you get it...)

A prime can also denote the derivative of a particular function, for example: (2x+3)", (x 3 )" , (sinx)" etc. Often the derivative is denoted using differentials, but we will not consider such a notation in this lesson.

Suppose that we have learned to understand the tasks. There is nothing left - to learn how to solve them.) Let me remind you again: finding the derivative is transformation of a function according to certain rules. These rules are surprisingly few.

To find the derivative of a function, you only need to know three things. Three pillars on which all differentiation rests. Here are the three whales:

1. Table of derivatives (differentiation formulas).

3. Derivative of a complex function.

Let's start in order. In this lesson, we will consider the table of derivatives.

Derivative table.

The world has an infinite number of functions. Among this set there are functions that are most important for practical application. These functions sit in all the laws of nature. From these functions, as from bricks, you can construct all the others. This class of functions is called elementary functions. It is these functions that are studied at school - linear, quadratic, hyperbola, etc.

Differentiation of functions "from scratch", i.e. based on the definition of the derivative and the theory of limits - a rather time-consuming thing. And mathematicians are people too, yes, yes!) So they simplified their lives (and us). They calculated derivatives of elementary functions before us. The result is a table of derivatives, where everything is ready.)

Here it is, this plate for the most popular functions. Left - elementary function, right - its derivative.

	Function y	Derivative of function y y"
1	C (constant)	C" = 0
2	x	x" = 1
3	x n (n is any number)	(x n)" = nx n-1
	x 2 (n = 2)	(x 2)" = 2x
4	sin x	(sinx)" = cosx
	cos x	(cos x)" = - sin x
	tg x
	ctg x
5	arcsin x
	arccos x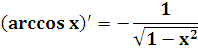
	arctg x
	arcctg x
4	a x
	e x
5	log a x
	ln x ( a = e)

I recommend paying attention to the third group of functions in this table of derivatives. The derivative of a power function is one of the most common formulas, if not the most common! Is the hint clear?) Yes, it is desirable to know the table of derivatives by heart. By the way, this is not as difficult as it might seem. Try to solve more examples, the table itself will be remembered!)

Finding the tabular value of the derivative, as you understand, is not the most difficult task. Therefore, very often in such tasks there are additional chips. Either in the formulation of the task, or in the original function, which does not seem to be in the table ...

Let's look at a few examples:

1. Find the derivative of the function y = x 3

There is no such function in the table. But there is a derivative of the power function in general view(third group). In our case, n=3. So we substitute the triple instead of n and carefully write down the result:

(x 3) " = 3 x 3-1 = 3x 2

That's all there is to it.

Answer: y" = 3x 2

2. Find the value of the derivative of the function y = sinx at the point x = 0.

This task means that you must first find the derivative of the sine, and then substitute the value x = 0 to this same derivative. It's in that order! Otherwise, it happens that they immediately substitute zero into the original function ... We are asked to find not the value of the original function, but the value its derivative. The derivative, let me remind you, is already a new function.

On the plate we find the sine and the corresponding derivative:

y" = (sinx)" = cosx

Substitute zero into the derivative:

y"(0) = cos 0 = 1

This will be the answer.

3. Differentiate the function:

What inspires?) There is not even close such a function in the table of derivatives.

Let me remind you that to differentiate a function is simply to find the derivative of this function. If you forget elementary trigonometry, finding the derivative of our function is quite troublesome. The table doesn't help...

But if we see that our function is cosine of a double angle, then everything immediately gets better!

Yes Yes! Remember that the transformation of the original function before differentiation quite acceptable! And it happens to make life a lot easier. According to the formula for the cosine of a double angle:

Those. our tricky function is nothing but y = cox. And this is a table function. We immediately get:

Answer: y" = - sin x.

Example for advanced graduates and students:

4. Find the derivative of a function:

There is no such function in the derivatives table, of course. But if you remember elementary mathematics, actions with powers... It is quite possible to simplify this function. Like this:

And x to the power of one tenth is already a tabular function! The third group, n=1/10. Directly according to the formula and write:

That's all. This will be the answer.

I hope that with the first whale of differentiation - the table of derivatives - everything is clear. It remains to deal with the two remaining whales. In the next lesson, we will learn the rules of differentiation.

In the coordinate plane hoy consider the graph of the function y=f(x). Fix a point M (x 0; f (x 0)). Let's give the abscissa x 0 increment Δх. We will get a new abscissa x 0 +Δx. This is the abscissa of the point N, and the ordinate will be f (х 0 +Δх). A change in the abscissa entailed a change in the ordinate. This change is called the increment of the function and denoted Δy.

Δy \u003d f (x 0 + Δx) - f (x 0). through dots M and N draw a secant MN, which forms an angle φ with positive axis direction Oh. Determine the tangent of the angle φ from right triangle MPN.

Let Δх tends to zero. Then the secant MN will tend to take the position of a tangent MT, and the angle φ will become a corner α . So the tangent of the angle α is the limit value of the tangent of the angle φ :

The limit of the ratio of the increment of the function to the increment of the argument, when the latter tends to zero, is called the derivative of the function at a given point:

The geometric meaning of the derivative lies in the fact that the numerical derivative of the function at a given point is equal to the tangent of the angle formed by the tangent drawn through this point to the given curve and the positive direction of the axis Oh:

Examples.

1. Find argument increment and function increment y= x2 if the initial value of the argument was 4 , and the new 4,01 .

Solution.

New argument value x \u003d x 0 + Δx. Substitute the data: 4.01=4+Δx, hence the increment of the argument Δх=4.01-4=0.01. The increment of a function, by definition, is equal to the difference between the new and previous values ​​of the function, i.e. Δy \u003d f (x 0 + Δx) - f (x 0). Since we have a function y=x2, then Δу\u003d (x 0 + Δx) 2 - (x 0) 2 \u003d (x 0) 2 + 2x 0 · Δx+(Δx) 2 - (x 0) 2 \u003d 2x 0 · ∆x+(∆x) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Answer: argument increment Δх=0.01; function increment Δу=0,0801.

It was possible to find the function increment in another way: Δy\u003d y (x 0 + Δx) -y (x 0) \u003d y (4.01) -y (4) \u003d 4.01 2 -4 2 \u003d 16.0801-16 \u003d 0.0801.

2. Find the angle of inclination of the tangent to the function graph y=f(x) at the point x 0, if f "(x 0) \u003d 1.

Solution.

The value of the derivative at the point of contact x 0 and is the value of the tangent of the slope of the tangent (the geometric meaning of the derivative). We have: f "(x 0) \u003d tgα \u003d 1 → α \u003d 45 °, because tg45°=1.

Answer: the tangent to the graph of this function forms an angle with the positive direction of the Ox axis, equal to 45°.

3. Derive the formula for the derivative of a function y=xn.

Differentiation is the act of finding the derivative of a function.

When finding derivatives, formulas are used that were derived on the basis of the definition of the derivative, in the same way as we derived the formula for the derivative degree: (x n)" = nx n-1.

Here are the formulas.

Derivative table it will be easier to memorize by pronouncing verbal formulations:

1. The derivative of a constant value is zero.

2. X stroke is equal to one.

3. The constant factor can be taken out of the sign of the derivative.

4. The derivative of a degree is equal to the product of the exponent of this degree by the degree with the same base, but the exponent is one less.

5. The derivative of the root is equal to one divided by two of the same roots.

6. The derivative of unity divided by x is minus one divided by x squared.

7. The derivative of the sine is equal to the cosine.

8. The derivative of cosine is equal to minus sine.

9. The derivative of the tangent is equal to one divided by the square of the cosine.

10. The derivative of the cotangent is minus one divided by the square of the sine.

We teach differentiation rules.

1. The derivative of the algebraic sum is equal to the algebraic sum of the derivative terms.

2. The derivative of the product is equal to the product of the derivative of the first factor by the second plus the product of the first factor by the derivative of the second.

3. The derivative of “y” divided by “ve” is equal to a fraction, in the numerator of which “y is a stroke multiplied by “ve” minus “y, multiplied by a stroke”, and in the denominator - “ve squared”.

4. A special case of the formula 3.

(\large\bf Function derivative)

Consider the function y=f(x), given on the interval (a,b). Let x- any fixed point interval (a,b), a Δx- an arbitrary number, such that the value x+Δx also belongs to the interval (a,b). This number Δx is called argument increment.

Definition. Function increment y=f(x) at the point x, corresponding to the increment of the argument Δx, let's call the number

Δy = f(x+Δx) - f(x).

We believe that Δx ≠ 0. Consider at a given fixed point x the ratio of the increment of the function at that point to the corresponding increment of the argument Δx

This relation will be called the difference relation. Since the value x we consider fixed, the difference relation is a function of the argument Δx. This function is defined for all argument values Δx, belonging to some sufficiently small neighborhood of the point ∆x=0, except for the point ∆x=0. Thus, we have the right to consider the question of the existence of a limit of the specified function for ∆x → 0.

Definition. Derivative function y=f(x) at a given fixed point x is called the limit ∆x → 0 differential relation, that is

Provided that this limit exists.

Designation. y (x) or f′(x).

The geometric meaning of the derivative: Derivative of function f(x) at this point x equal to the tangent of the angle between the axis Ox and a tangent to the graph of this function at the corresponding point:

f′(x 0) = \tgα.

The mechanical meaning of the derivative: The derivative of the path with respect to time is equal to the speed of the rectilinear movement of the point:

Line tangent equation y=f(x) at the point M0 (x0,y0) takes the form

y-y 0 = f (x 0) (x-x 0).

The normal to the curve at some point is the perpendicular to the tangent at the same point. If a f′(x 0)≠ 0, then the equation of the normal to the line y=f(x) at the point M0 (x0,y0) is written like this:

The concept of differentiability of a function

Let the function y=f(x) defined on some interval (a,b), x- some fixed value of the argument from this interval, Δx- any increment of the argument such that the value of the argument x+Δx ∈ (a, b).

Definition. Function y=f(x) is called differentiable at a given point x if increment Δy this function at the point x, corresponding to the increment of the argument Δx, can be represented as

Δy = A Δx +αΔx,

where A is some number independent of Δx, a α - argument function Δx, which is infinitely small at ∆x → 0.

Since the product of two infinitesimal functions αΔx is an infinitesimal higher order than Δx(property 3 of infinitesimal functions), we can write:

∆y = A ∆x +o(∆x).

Theorem. In order for the function y=f(x) was differentiable at a given point x, it is necessary and sufficient that it has a finite derivative at this point. Wherein A=f′(x), that is

Δy = f′(x) Δx +o(Δx).

The operation of finding the derivative is usually called differentiation.

Theorem. If the function y=f(x) x, then it is continuous at that point.

Comment. From the continuity of the function y=f(x) at this point x, generally speaking, it does not follow that the function is differentiable f(x) at this point. For example, the function y=|x|- continuous at a point x=0, but has no derivative.

The concept of a function differential

Definition. function differential y=f(x) is called the product of the derivative of this function and the increment of the independent variable x:

dy = y′ ∆x, df(x) = f′(x) ∆x.

For function y=x we get dy=dx=x'Δx = 1 Δx= Δx, that is dx=Δx- the differential of an independent variable is equal to the increment of this variable.

Thus, we can write

dy = y′dx, df(x) = f′(x)dx

Differential dy and increment Δy functions y=f(x) at this point x, both corresponding to the same increment of the argument Δx are, in general, not equal to each other.

The geometric meaning of the differential: The differential of a function is equal to the increment of the ordinate of the tangent to the graph of the given function when the argument is incremented Δx.

Differentiation rules

Theorem. If each of the functions u(x) and v(x) differentiable at a given point x, then the sum, difference, product and quotient of these functions (quotient provided that v(x)≠ 0) are also differentiable at this point, and the following formulas hold:

Consider a complex function y=f(φ(x))≡ F(x), where y=f(u), u=φ(x). In this case u called intermediate argument, x - independent variable.

Theorem. If a y=f(u) and u=φ(x) are differentiable functions of their arguments, then the derivative of the complex function y=f(φ(x)) exists and is equal to the product of this function with respect to the intermediate argument and the derivative of the intermediate argument with respect to the independent variable, i.e.

Comment. For a complex function that is a superposition of three functions y=F(f(φ(x))), the differentiation rule has the form

y′ x = y′ u u′ v v′ x,

where functions v=φ(x), u=f(v) and y=F(u) are differentiable functions of their arguments.

Theorem. Let the function y=f(x) is increasing (or decreasing) and continuous in some neighborhood of the point x0. Let, in addition, this function be differentiable at the indicated point x0 and its derivative at this point f′(x 0) ≠ 0. Then in some neighborhood of the corresponding point y0=f(x0) the inverse for y=f(x) function x=f -1 (y), and the indicated inverse function is differentiable at the corresponding point y0=f(x0) and for its derivative at this point y the formula is valid

Derivative table

Invariance of the form of the first differential

Consider the differential of a complex function. If a y=f(x), x=φ(t) are differentiable functions of their arguments, then the derivative of the function y=f(φ(t)) is expressed by the formula

y′ t = y′ x x′ t.

By definition dy=y't dt, then we get

dy = y′ t dt = y′ x x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

So, we have proven

Property of invariance of the form of the first differential of a function: as in the case when the argument x is an independent variable, and in the case when the argument x is itself a differentiable function of the new variable, the differential dy functions y=f(x) is equal to the derivative of this function, multiplied by the differential of the argument dx.

Application of the differential in approximate calculations

We have shown that the differential dy functions y=f(x), generally speaking, is not equal to the increment Δy this function. Nevertheless, up to an infinitely small function of a higher order of smallness than Δx, the approximate equality

∆y ≈ dy.

The ratio is called the relative error of the equality of this equality. Because ∆y-dy=o(∆x), then relative error of this equality becomes arbitrarily small as |Δх|.

Given that Δy=f(x+δx)-f(x), dy=f′(x)Δx, we get f(x+δx)-f(x) ≈ f′(x)Δx or

f(x+δx) ≈ f(x) + f′(x)Δx.

This approximate equality allows with an error o(Δx) replace function f(x) in a small neighborhood of a point x(i.e. for small values Δx) a linear function of the argument Δx standing on the right side.

Derivatives of higher orders

Definition. The second derivative (or second order derivative) of the function y=f(x) is called the derivative of its first derivative.

Notation for the second derivative of a function y=f(x):

Mechanical meaning of the second derivative. If the function y=f(x) describes the law of motion material point in a straight line, then the second derivative f″(x) is equal to the acceleration of the moving point at time x.

The third and fourth derivatives are defined similarly.

Definition. n-th derivative (or derivative n th order) functions y=f(x) called the derivative of it n-1-th derivative:

y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.

Designations: y″′, y IV, y V etc.

The operation of finding a derivative is called differentiation.

As a result of solving problems of finding derivatives of the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716) were the first to work in the field of finding derivatives.

Therefore, in our time, in order to find the derivative of any function, it is not necessary to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but only need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.

To find the derivative, you need an expression under the stroke sign break down simple functions and determine what actions (product, sum, quotient) these functions are related. Further, we find the derivatives of elementary functions in the table of derivatives, and the formulas for the derivatives of the product, sum and quotient - in the rules of differentiation. The table of derivatives and differentiation rules are given after the first two examples.

Example 1 Find the derivative of a function

Solution. From the rules of differentiation we find out that the derivative of the sum of functions is the sum of derivatives of functions, i.e.

From the table of derivatives, we find out that the derivative of "X" is equal to one, and the derivative of the sine is cosine. We substitute these values ​​in the sum of derivatives and find the derivative required by the condition of the problem:

Example 2 Find the derivative of a function

Solution. Differentiate as a derivative of the sum, in which the second term with a constant factor, it can be taken out of the sign of the derivative:

If there are still questions about where something comes from, they, as a rule, become clear after reading the table of derivatives and the simplest rules of differentiation. We are going to them right now.

Table of derivatives of simple functions

1. Derivative of a constant (number). Any number (1, 2, 5, 200...) that is in the function expression. Always zero. This is very important to remember, as it is required very often
2. Derivative of the independent variable. Most often "x". Always equal to one. This is also important to remember
3. Derivative of degree. When solving problems, you need to convert non-square roots to a power.
4. Derivative of a variable to the power of -1
5. Derivative square root
6. Sine derivative
7. Cosine derivative
8. Tangent derivative
9. Derivative of cotangent
10. Derivative of the arcsine
11. Derivative of arc cosine
12. Derivative of arc tangent
13. Derivative of the inverse tangent
14. Derivative of natural logarithm
15. Derivative of a logarithmic function
16. Derivative of the exponent
17. Derivative of exponential function

Differentiation rules

1. Derivative of the sum or difference
2. Derivative of a product
2a. Derivative of an expression multiplied by a constant factor
3. Derivative of the quotient
4. Derivative of a complex function

Rule 1If functions

are differentiable at some point , then at the same point the functions

and

those. the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions.

Consequence. If two differentiable functions differ by a constant, then their derivatives are, i.e.

Rule 2If functions

are differentiable at some point , then their product is also differentiable at the same point

and

those. the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other.

Consequence 1. The constant factor can be taken out of the sign of the derivative:

Consequence 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each of the factors and all the others.

For example, for three multipliers:

Rule 3If functions

differentiable at some point and , then at this point their quotient is also differentiable.u/v , and

those. the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator.

Where to look on other pages

When finding the derivative of the product and the quotient in real problems, it is always necessary to apply several differentiation rules at once, so more examples on these derivatives are in the article."The derivative of a product and a quotient".

Comment. You should not confuse a constant (that is, a number) as a term in the sum and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. it typical mistake, which occurs on initial stage learning derivatives, but as they solve several one-two-component examples, the average student no longer makes this mistake.

And if, when differentiating a product or a quotient, you have a term u"v, wherein u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (such a case is analyzed in example 10).

Another common mistake is the mechanical solution of the derivative of a complex function as the derivative of a simple function. That's why derivative of a complex function devoted to a separate article. But first we will learn to find derivatives of simple functions.

Along the way, you can not do without transformations of expressions. To do this, you may need to open in new windows manuals Actions with powers and roots and Actions with fractions .

If you are looking for solutions to derivatives with powers and roots, that is, when the function looks like , then follow the lesson " Derivative of the sum of fractions with powers and roots".

If you have a task like , then you are in the lesson "Derivatives of simple trigonometric functions".

Step by step examples - how to find the derivative

Example 3 Find the derivative of a function

Solution. We determine the parts of the function expression: the entire expression represents the product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the product differentiation rule: the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other:

Next, we apply the rule of differentiation of the sum: the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum, the second term with a minus sign. In each sum, we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, "x" turns into one, and minus 5 - into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We get the following values ​​of derivatives:

We substitute the found derivatives into the sum of products and obtain the derivative of the entire function required by the condition of the problem:

Example 4 Find the derivative of a function

Solution. We are required to find the derivative of the quotient. We apply the formula for differentiating a quotient: the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator. We get:

We have already found the derivative of the factors in the numerator in Example 2. Let's also not forget that the product, which is the second factor in the numerator in the current example, is taken with a minus sign:

If you are looking for solutions to such problems in which you need to find the derivative of a function, where there is a continuous pile of roots and degrees, such as, for example, then welcome to class "The derivative of the sum of fractions with powers and roots" .

If you need to learn more about derivatives of sines, cosines, tangents and others trigonometric functions, that is, when the function looks like , then you have a lesson "Derivatives of simple trigonometric functions" .

Example 5 Find the derivative of a function

Solution. In this function, we see a product, one of the factors of which is the square root of the independent variable, with the derivative of which we familiarized ourselves in the table of derivatives. According to the product differentiation rule and the tabular value of the derivative of the square root, we get:

Example 6 Find the derivative of a function

Solution. In this function, we see the quotient, the dividend of which is the square root of the independent variable. According to the rule of differentiation of the quotient, which we repeated and applied in example 4, and the tabular value of the derivative of the square root, we get:

To get rid of the fraction in the numerator, multiply the numerator and denominator by .

When a person has taken the first independent steps in the study of mathematical analysis and begins to ask uncomfortable questions, then it is no longer so easy to get off with the phrase that “ differential calculus found in cabbage. Therefore, it is time to be determined and solve the mystery of the birth of tables of derivatives and differentiation rules. Started in the article about the meaning of the derivative, which I highly recommend for study, because there we just considered the concept of a derivative and started clicking tasks on the topic. The same lesson has a pronounced practical orientation, moreover,

the examples considered below, in principle, can be mastered purely formally (for example, when there is no time / desire to delve into the essence of the derivative). It is also highly desirable (but again not necessary) to be able to find derivatives using the "usual" method - at least at the level of two basic classes: How to find the derivative? and Derivative of a complex function.

But without something, which is now definitely indispensable, it is without function limits. You must UNDERSTAND what a limit is and be able to solve them, at least at an intermediate level. And all because the derivative

function at a point is defined by the formula:

I remind you of the designations and terms: they call argument increment;

– function increment;

- these are SINGLE symbols (“delta” cannot be “torn off” from “X” or “Y”).

Obviously, is a "dynamic" variable, is a constant and the result of calculating the limit - number (sometimes - "plus" or "minus" infinity).

As a point, you can consider ANY value belonging to domains a function that has a derivative.

Note: the clause "in which the derivative exists" - generally significant.! So, for example, the point, although it enters the domain of the function, but the derivative

does not exist there. Therefore the formula

not applicable at the point

and a shortened wording without a reservation would be incorrect. Similar facts are also valid for other functions with "breaks" in the graph, in particular, for the arcsine and arccosine.

Thus, after replacing , we obtain the second working formula:

Pay attention to an insidious circumstance that can confuse the teapot: in this limit, "x", being itself an independent variable, plays the role of an extra, and "dynamics" is again set by the increment. The result of limit calculation

is the derivative function.

Based on the foregoing, we formulate the conditions of two typical problems:

- Find derivative at a point using the definition of a derivative.

- Find derivative function using the definition of a derivative. This version, according to my observations, occurs much more often and will be given the main attention.

The fundamental difference between the tasks is that in the first case it is required to find the number (optionally infinity), and in the second

function . In addition, the derivative may not exist at all.

How ?

Make a ratio and calculate the limit.

Where did table of derivatives and differentiation rules ? With a single limit

Seems like magic, but

reality - sleight of hand and no fraud. On the lesson What is a derivative? I started looking concrete examples, where, using the definition, I found the derivatives of the linear and quadratic function. For the purpose of cognitive warm-up, we will continue to disturb derivative table, honing the algorithm and technical solutions:

In fact, it is required to prove a special case of the derivative of a power function, which usually appears in the table: .

The solution is technically formalized in two ways. Let's start with the first, already familiar approach: the ladder starts with a plank, and the derivative function starts with a derivative at a point.

Consider some (concrete) point belonging to domains a function that has a derivative. Set the increment at this point (of course, not beyond o / o - z) and compose the corresponding increment of the function:

Let's calculate the limit:

Uncertainty 0:0 is eliminated by a standard technique considered as far back as the first century BC. multiply

numerator and denominator per adjoint expression :

The technique for solving such a limit is discussed in detail in the introductory lesson. about the limits of functions.

Since ANY point of the interval can be chosen as

Then, by substituting, we get:

Once again, let's rejoice at the logarithms:

Find the derivative of the function using the definition of the derivative

Solution: Let's consider a different approach to spinning up the same task. It is exactly the same, but more rational in terms of design. The idea is to get rid of the

subscript and use a letter instead of a letter.

Consider an arbitrary point belonging to domains function (interval), and set the increment in it. And here, by the way, as in most cases, you can do without any reservations, since the logarithmic function is differentiable at any point in the domain of definition.

Then the corresponding function increment is:

Let's find the derivative:

Simplicity of design is balanced by confusion, which can

arise in beginners (and not only). After all, we are used to the fact that the letter “X” changes in the limit! But here everything is different: - an antique statue, and - a living visitor, briskly walking along the corridor of the museum. That is, “x” is “like a constant”.

I will comment on the elimination of uncertainty step by step:

(1) Using the property of the logarithm.

(2) Divide the numerator by the denominator in parentheses.

(3) In the denominator we artificially multiply and divide by "x" so that

take advantage of the wonderful , while as infinitesimal performs.

Answer: By definition of derivative:

Or in short:

I propose to independently construct two more tabular formulas:

Find derivative by definition

AT this case it is convenient to immediately reduce the increment to a common denominator. Sample Sample completing the task at the end of the lesson (the first method).

Find derivative by definition

And here everything must be reduced to a remarkable limit. The solution is framed in the second way.

Similarly, a number of other tabular derivatives. Full list can be found in a school textbook, or, for example, the 1st volume of Fichtenholtz. I don’t see much point in rewriting from books and proofs of the rules of differentiation - they are also generated

formula .

Let's move on to real-life tasks: Example 5

Find the derivative of a function , using the definition of the derivative

Solution: use the first style. Let's consider some point that belongs to, and set the increment of the argument in it. Then the corresponding function increment is:

Perhaps some readers have not yet fully understood the principle by which an increment should be made. We take a point (number) and find the value of the function in it: , that is, into the function

instead of "x" should be substituted. Now we take

Composed Function Increment it is beneficial to immediately simplify. What for? Facilitate and shorten the solution of the further limit.

We use formulas, open brackets and reduce everything that can be reduced:

The turkey is gutted, no problem with the roast:

Eventually:

Since any real number can be chosen as the quality, we make the substitution and get .

Answer : by definition.

For verification purposes, we find the derivative using the rules

differentiations and tables:

It is always useful and pleasant to know the correct answer in advance, so it is better to mentally or on a draft differentiate the proposed function in a “quick” way at the very beginning of the solution.

Find the derivative of a function by the definition of the derivative

This is a do-it-yourself example. The result lies on the surface:

Back to Style #2: Example 7

Let's find out immediately what should happen. By the rule of differentiation of a complex function:

Decision: consider an arbitrary point belonging to, set the increment of the argument in it and make the increment

Let's find the derivative:

(1) We use the trigonometric formula

(2) Under the sine we open the brackets, under the cosine we give like terms.

(3) Under the sine we reduce the terms, under the cosine we divide the numerator by the denominator term by term.

(4) Due to the oddness of the sine, we take out the "minus". Under cosine

indicate that the term .

(5) We artificially multiply the denominator to use first wonderful limit. Thus, the uncertainty is eliminated, we comb the result.

Answer: by definition As you can see, the main difficulty of the problem under consideration rests on

the complexity of the limit itself + a slight originality of the packaging. In practice, both methods of design are encountered, so I describe both approaches in as much detail as possible. They are equivalent, but still, in my subjective impression, it is more expedient for dummies to stick to the 1st option with “X zero”.

Using the definition, find the derivative of the function

This is a task for independent decision. The sample is formatted in the same spirit as the previous example.

Let's analyze a rarer version of the problem:

Find the derivative of a function at a point using the definition of a derivative.

First, what should be the bottom line? Number Calculate the answer in the standard way:

Decision: from the point of view of clarity, this task is much simpler, since in the formula instead of

considered a specific value.

We set an increment at the point and compose the corresponding increment of the function:

Calculate the derivative at a point:

We use a very rare formula for the difference of tangents and for the umpteenth time we reduce the solution to the first

amazing limit:

Answer: by definition of the derivative at a point.

The task is not so difficult to solve and “in general terms” - it is enough to replace the nails or simply, depending on the design method. In this case, of course, you get not a number, but a derivative function.

Example 10 Using the definition, find the derivative of a function at the point

This is a do-it-yourself example.

The final bonus task is intended primarily for students with in-depth study of mathematical analysis, but it will not hurt everyone else either:

Will the function be differentiable at the point?

Solution: It is obvious that a piecewise given function is continuous at a point, but will it be differentiable there?

The solution algorithm, and not only for piecewise functions, is as follows:

1) Find the left-hand derivative at a given point: .

2) Find the right-hand derivative at the given point: .

3) If one-sided derivatives are finite and coincide:

, then the function is differentiable at the point and

geometrically, there is a common tangent here (see the theoretical part of the lesson Definition and meaning of derivative).

If received two different meanings: (one of which may be infinite), then the function is not differentiable at a point.

If both one-sided derivatives are equal to infinity

(even if they have different signs), then the function does not

is differentiable at a point, but there exists an infinite derivative and a common vertical tangent to the graph (see Example 5 of lessonNormal Equation) .