고립된 특이점을 찾는 방법. Laurent 계열 분리된 특이점 및 분류

두 개의 자율 미분 방정식 시스템으로 설명되는 모델입니다.

위상 평면. 위상 초상화. 등각선법. 주요 등각선. 안정된 상태 안정성. 선형 시스템. 키 포인트 유형: 노드, 안장, 초점, 센터. 예시: 화학 반응첫 주문.

생물학적 시스템의 특성에 대한 정성적 모델링에 대한 가장 흥미로운 결과는 두 가지 미분 방정식의 모델에서 얻었습니다. 위상 평면. 두 개의 자율 상미분 방정식 시스템을 고려하십시오. 일반보기

(4.1)

P(x,y), Q(x,y)- 일부 도메인에서 정의된 연속 함수 G유클리드 평면( x,y- 데카르트 좌표) 및 이 영역에서 첫 번째보다 낮지 않은 차수의 연속 도함수를 가집니다.

지역 G무제한 또는 제한적일 수 있습니다. 변수인 경우 x, y특정한 생물학적 의미(물질의 농도, 종의 풍부함)를 가지며, 가장 흔히 지역 G오른쪽 절반 평면의 양의 사분면:

0 £ 엑스< ¥ ,0 £ 와이< ¥ .

물질의 농도 또는 종의 풍부함은 또한 선박의 부피 또는 서식지 면적에 의해 위에서 제한될 수 있습니다. 그러면 변수의 범위는 다음과 같은 형식을 갖습니다.

0 £ 엑스< x 0 , 0 £ 와이< y 0 .

변수 x, y시스템의 각 상태가 한 쌍의 변수 값에 해당하도록 방정식 (4.1) 시스템에 따른 시간 변화 ( x, y).

반대로, 각 변수 쌍에 대해( x, y) 시스템의 특정 상태에 해당합니다.

변수 값이 그려지는 좌표축이 있는 평면을 고려하십시오. x,y. 모든 포인트 중이 평면은 시스템의 특정 상태에 해당합니다. 이러한 평면을 위상 평면이라고 하며 시스템의 모든 상태의 전체를 나타냅니다. 점 M(x, y)을 묘사 또는 대표 점이라고 합니다.

초기 시간에 하자 t=t점 좌표를 나타내는 0 중 0 (엑스(티 0),와이(티 0)). 다음 순간마다 티변수 값의 변화에 ​​따라 묘사점이 이동합니다. 엑스(티),와이(티). 포인트 세트 중(엑스(티), y(t)) 위상 평면에서, 그 위치는 시간이 지남에 따라 변수를 변경하는 과정에서 시스템의 상태에 해당합니다. x(t), y(t)방정식 (4.1)에 따르면 위상 궤적.

변수의 다양한 초기 값에 대한 위상 궤적 세트는 시스템의 쉽게 볼 수 있는 "초상화"를 제공합니다. 건물 위상 초상화변수의 변화 특성에 대한 결론을 도출할 수 있습니다. x, y원래 연립방정식의 해석적 해를 모른 채(4.1).

위상 초상화를 묘사하려면 위상 평면의 각 지점에서 시스템 궤적에 대한 방향 벡터 필드를 구성해야 합니다. 증분을 지정하여디 t>0,우리는 해당 증분을 얻습니다 디 엑스그리고 디 와이표현식에서:

디 x=P(x,y)디 티,

디 y=Q(x,y)디 티.

벡터 방향 dy/dx점에서 ( x, y) 함수의 부호에 따라 다름 P(x, y), Q(x, y)그리고 다음과 같은 표로 주어질 수 있습니다.

P(x,y)>0,Q(x,y)>0
피(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
피(x,y)<0,Q(x,y)>0

.(4.2)

이 방정식의 해 y=y(x, c), 또는 암시적으로 에프(x,y)=c,어디 와 함께는 적분 상수이며 방정식 (4.2)의 적분 곡선 제품군을 제공합니다. 위상 궤적비행기의 시스템(4.1) x, y.

등각선법

위상 초상화를 구성하려면 다음을 사용합니다. 등각선법 -하나의 특정 각도에서 적분 곡선을 교차하는 위상 평면에 선이 그려집니다. 등사선 방정식은 (4.2)에서 쉽게 얻을 수 있습니다. 넣어보자

어디 하지만– 일정한 상수. 의미 하지만위상 궤적에 대한 접선 기울기의 접선을 나타내며 다음 값을 취할 수 있습니다. -¥ +로 ¥ . 대신에 대체 dy/dx(4.2)에서 수량 하지만우리는 등사선 방정식을 얻습니다.

.(4.3)

방정식 (4.3)은 평면의 각 점에서 해당 적분 곡선에 대한 유일한 접선을 결정합니다. 단, 다음과 같은 점은 제외됩니다. 피(x,y)= 0, Q (x,y) = 0 , 도함수의 값이 무한이 되기 때문에 접선의 방향이 무한이 됩니다.

.

이 점은 모든 등각선의 교차점입니다. 특별한 점.변수의 시간 도함수가 동시에 사라집니다. 엑스그리고 와이.

따라서 특이점에서 변수의 변화율은 0과 같습니다. 따라서 위상 궤적(4.2)의 미분 방정식의 특이점은 다음과 같습니다. 시스템의 정지 상태(4.1) 및 그 좌표는 변수의 고정 값입니다 x, y.

특히 관심 있는 것은 주요 등각선:

dy/dx=0, P(x,y)=0 – 수평 접선의 등각선 및

dy/dx=¥ , 문(x,y)=0 – 수직 접선의 등각선.

주요 등각선을 구성하고 교차점을 찾는 방법 (x,y), 다음 조건을 충족하는 좌표:

따라서 위상 궤적에 대한 접선의 방향이 부정확한 위상 평면의 모든 등각선의 교차점을 찾을 수 있습니다. 그것 - 특이점, 해당 시스템의 정지 상태(그림 4.2).

시스템(4.1)에는 위상 평면에 있는 주요 등각선의 교차점이 있는 만큼 많은 정지 상태가 있습니다.

각 위상 궤적은 동일한 상태를 통과하고 시간 기준의 시작 부분에서만 서로 다른 역학 시스템의 운동 집합에 해당합니다.

코시 정리의 조건이 충족되면 공간의 각 점을 통해 x, y, t단일 적분 곡선을 통과합니다. 자율성 덕분에 위상 궤적도 마찬가지입니다. 고유한 위상 궤적이 위상 평면의 각 지점을 통과합니다.

정상 상태 안정성

시스템이 평형 상태에 있도록 하십시오.

그런 다음 대표 점은 정의에 따라 시스템의 특이점 중 하나에 위치합니다.

.

특이점의 안정 여부는 대표점이 정지 상태에서 약간의 편차를 가지고 이탈하는지 여부에 따라 결정됩니다. 두 개의 방정식 시스템에 적용할 때 언어의 안정성 정의이자형, 디다음과 같이.

평형 상태는 평형 상태에서 벗어난 주어진 영역에 대해 안정적입니다. (이자형 )영역을 지정할 수 있습니다 디 (이자형 ), 평형 상태를 둘러싸고 영역 내부에서 시작되는 궤적이 없는 특성을 가지고 있습니다. 디 , 국경에 도달하지 않습니다 이자형 . (그림 4.4)

대규모 시스템의 경우 - 거친 시스템 – 방정식의 종류를 조금만 바꿔도 거동의 성질이 변하지 않고, 정지상태 부근에서의 거동의 종류에 대한 정보는 원문을 연구하는 것이 아니라 단순화하여 얻을 수 있다. 선형화체계.

선형 시스템.

2인 체제를 고려하라 선형 방정식:

.(4.4)

여기 a, b, c, d- 상수, x, y- 위상 평면의 직교 좌표.

일반적인 솔루션은 다음과 같은 형식으로 찾을 수 있습니다.

.(4.5)

이 식을 (4.4)에 대입하고 다음과 같이 줄입니다. 이자형 엘 티:

(4.6)

미지수가 있는 대수 방정식(4.6) 에이, 비미지수의 계수로 구성된 행렬식이 0인 경우에만 0이 아닌 솔루션을 갖습니다.

.

이 행렬식을 확장하여 시스템의 특성 방정식을 얻습니다.

.(4.7)

이 방정식의 솔루션은 표시기의 값을 제공합니다엘 1,2 , 0이 아닌 값이 가능한 ㅏ그리고 비방정식 (4.6)의 솔루션. 이러한 값은

.(4.8)

급진적 표현이 음수이면엘 1,2 복소수 켤레. 방정식(4.7)의 두 근 모두 0이 아닌 실수부를 갖고 다중 근이 없다고 가정합니다. 그런 다음 시스템 (4.4)의 일반 솔루션은 지수와 지수의 선형 조합으로 나타낼 수 있습니다.엘 1 , 엘 2 :

(4.9)

위상 평면에서 시스템의 가능한 궤적의 특성을 분석하기 위해 다음을 사용합니다. 선형 균질 좌표 변환,시스템을 가져올 것입니다 표준 형식:

,(4.10)

이는 원래 시스템(4.4)에 비해 위상 평면에서 보다 편리한 표현을 허용합니다. 새로운 좌표를 소개합니다ξ , η 공식에 따르면:

(4.1)

실수부가 0이 아닌 경우 선형 대수학 과정에서 알 수 있습니다.엘 1 , 엘 2 변환(4.11)의 도움으로 원래 시스템(4.4)은 항상 표준 형식(4.10)으로 변환될 수 있으며 위상 평면에서의 동작을 연구할 수 있습니다.ξ , η . 여기에 나타날 수 있는 다양한 경우를 고려하십시오.

뿌리 λ 1 , λ 2 – 유효하고 동일한 부호의

이 경우 변환 계수는 실수이며 실제 평면에서 이동합니다.x,y실제 평면 ξ, η. 방정식 (4.10)의 두 번째를 첫 번째로 나누면 다음을 얻습니다.:

.(4.12)

이 방정식을 통합하면:

어디 .(4.13)

λ로 이해하는 데 동의합시다. 2 우리 추론의 일반성을 위반하지 않는 큰 계수를 갖는 특성 방정식의 근. 그런 다음 고려중인 경우 근 λ 1 , λ2 – 유효하고 동일한 부호의ㅏ>1 , 그리고 우리는 포물선 유형의 적분 곡선을 다루고 있습니다.

모든 적분 곡선(축 제외 η 에 해당하는 ) 축의 원점에서 터치 ξ, 이는 또한 방정식(4.11)의 적분 곡선입니다. 좌표의 원점은 특이점입니다.

이제 위상 궤적을 따라 대표점의 운동 방향을 알아 보겠습니다. 만약 λ 1 , λ 2 그러면 방정식(4.10), |ξ|, |η|에서 볼 수 있듯이 음수입니다. 시간이 지남에 따라 감소합니다. 대표점은 원점에 접근하지만 결코 도달하지 않습니다. 그렇지 않으면 하나의 위상 궤적이 위상 평면의 각 점을 통과한다는 코시의 정리와 모순됩니다.

마치 포물선의 한 가족처럼 적분곡선이 지나는 특이점 원점을 통과하는 노드를 노드라고 합니다(그림. 4.5)

λ에서의 매듭형 평형상태 1 , λ 2 < 0 대표점이 좌표의 원점을 향해 모든 적분 곡선을 따라 이동하기 때문에 Lyapunov에 따르면 안정적입니다. 그것 안정적인 매듭. 만약 λ 1 , λ 2 > 0, 그럼 |ξ|, |η| 시간이 지남에 따라 증가하고 대표점이 원점에서 멀어집니다. 이 경우 특이점– 불안정한 노드 .

위상 평면에서 x, y 적분 곡선의 동작의 일반적인 질적 특성은 유지되지만 적분 곡선에 대한 접선은 좌표 축과 일치하지 않습니다. 이러한 접선의 경사각은 계수의 비율에 의해 결정됩니다. α , β , γ , δ 방정식(4.11)에서.

뿌리 λ 1 , λ 2 유효하며 다른 기호가 있습니다.

다음에서 변환좌표 x,y 좌표로 ξ, η 다시 진짜. 정규 변수에 대한 방정식은 다시 (4.10) 형식을 갖지만 이제 기호 λ 1 , λ 2 다른. 위상 궤적 방정식은 다음과 같은 형식을 갖습니다.:

어디 , (4.14)

통합 (4.14), 우리는

(4.15)

그것 방정식은 쌍곡선 유형의 곡선 제품군을 정의합니다. 여기서 두 좌표 축점근선(~에서 ㅏ=1 우리는 이등변 쌍곡선의 가족을 가질 것입니다). 이 경우 좌표축도 적분 곡선입니다.– 이것은 원점을 통과하는 유일한 적분 곡선이 될 것입니다. 각그 중 3단계 궤적으로 구성: 평형 상태를 향한(또는 평형 상태로부터 멀어지는) 두 가지 움직임과 평형 상태로부터의 움직임. 기타 모든 적분 곡선– 원점을 통과하지 않는 쌍곡선(그림. 4.6) 이 특이점을 "안장 ». 산 안장 근처의 레벨 라인은 안장 근처의 위상 궤적처럼 동작합니다.

평형 상태 근처의 위상 궤적을 따라 대표점의 운동 특성을 고려합시다. 예를 들어,λ 1 >0 , λ 2<0 . 그런 다음 축에 배치된 대표점 ξ , 원점에서 멀어지고 축에 배치됩니다. η – 무한정 좌표의 원점에 접근합니다., 한정된 시간에 도달하지 않고. 대표점이 초기 순간에 있는 모든 곳(특이점과 점근선 상의 점 제외) η =0), 처음에는 적분 곡선 중 하나를 따라 특이점을 향해 움직이더라도 결국 평형 상태에서 멀어집니다..

그것은 분명하다 안장형 특이점은 항상 불안정 . 점근선에서 특별히 선택된 초기 조건에서만η =0 시스템은 평형 상태에 접근합니다. 그러나 이것은 시스템이 불안정하다는 주장과 모순되지 않습니다. 계산하면, 위상 평면에 있는 시스템의 모든 초기 상태가 동일할 가능성이 있는 경우 해당 방향으로의 이동에 해당하는 초기 상태의 확률에게 특이점은 0과 같습니다. 따라서 실제 움직임은 시스템을 평형 상태에서 제거합니다.좌표로 돌아가기x,y,우리는 원점 주위의 궤적 움직임의 본질에 대한 동일한 질적 그림을 얻습니다.

노드와 안장의 고려된 경우 사이의 경계는 다음과 같습니다.언제 예를 들어 특성 지표 중 하나 λ 1 , 시스템의 행렬식에서 발생하는 소멸- 표현 adbc=0(공식 4.8 참조 ). 이 경우 방정식(4.4)의 우변 계수는 서로 비례합니다.:

시스템은 평형 상태를 위해 선의 모든 점을 가지고 있습니다.:

나머지 적분 곡선은 기울기가 있는 평행선 모음입니다. , 대표 포인트는 특성 방정식 λ의 두 번째 루트의 부호에 따라 평형 상태에 접근하거나 평형 상태에서 멀어집니다. 2 = ㄱ+ㄹ.(그림 4. 7 ) 이 경우 평형상태의 좌표는 변수의 초기값에 의존한다.

뿌리 λ 1 , λ 2 – 복잡한결합한

이 경우 실제엑스그리고 와이우리는 할 것이다 복잡한 켤레를 가지고 ξ , η (4.10) . 그러나 중간 변환을 하나 더 도입함으로써 이 경우 고려 사항을 실제 선형 동차 변환으로 줄이는 것도 가능합니다. 넣어보자:

(4.16)

어디 에이, ㄴ,그리고 유, v – 실제 가치. 로부터의 변환임을 알 수 있다.x,y에게 유, v 우리의 가정 하에서 는 실수, 선형, 0이 아닌 행렬식으로 동질적입니다. 방정식으로 인해(4.10, 4.16) 다음이 있습니다.

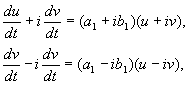
어디

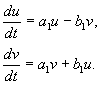(4.17)

방정식의 두 번째를 첫 번째 방정식으로 나누기, 우리는 다음을 얻습니다.

통합하기 쉬운 것, 극좌표계로 전환하면 (아르 자형, φ ) . 교체 후우리는 어디에서 얻습니다:

.(4.18)

따라서 위상 평면에서유, v우리는 각각의 로그 나선의 가족을 다루고 있습니다.원점의 점근점.나선 형태를 갖는 모든 적분곡선의 점근점인 특이점, 중첩된 친구친구, 전화 집중하다 ( 그림 4.8 ) .

위상 궤적을 따라 대표점의 움직임의 특성을 고려합시다. 방정식 (4.17)의 첫 번째 곱하기유, 그리고 두 번째로 V추가하면 다음을 얻습니다.

어디에

허락하다 ㅏ 1 < 0 (ㅏ 1 = 답장λ ) . 그런 다음 대표점은 유한한 시간 내에 원점에 도달하지 않고 계속해서 원점에 접근합니다. 이것은 위상 궤적이 비틀린 나선이고 감쇠된 진동에 해당한다는 것을 의미합니다.변수. 그것 - 꾸준한 초점 .

스테이블 포커스의 경우, 스테이블 노드의 경우와 마찬가지로 리아푸노프 조건을 만족할 뿐만 아니라 더 엄격한 요구 사항도 만족합니다. 즉, 초기 편차에 대해 시스템은 결국 평형 위치에 원하는 만큼 가깝게 복귀합니다. 초기 편차가 증가하지 않을 뿐만 아니라 0이 되는 경향이 있는 이러한 안정성을 호출합니다. 절대 안정성 .

만약 공식에 (4.18) ㅏ 1 >0 , 그러면 대표점이 원점에서 멀어지고 우리는 불안정한 초점 . 비행기에서 이동할 때유, v위상 평면으로엑스, 와이나선도 나선으로 남지만 변형됩니다.

다음 경우를 고려하십시오.ㅏ 1 =0 . 평면의 위상 궤적유, v원이있을 것입니다 비행기에서x,y맞춤 타원:

따라서1=0 특별한 포인트를 통해x= 0,y= 0 적분 곡선이 통과하지 않습니다. 적분곡선이 폐곡선, 특히 타원이 서로 끼워져 있고 그 특이점을 둘러싸고 있는 이러한 고립된 특이점을 중심이라고 한다.

따라서 특성방정식(4.7)의 근의 성질에 따라 6가지 평형이 가능하다. 평면의 위상 궤적 보기 x, y이 6가지 경우에 대해 그림 1에 나와 있습니다. 4.9.

쌀. 4.9.선형 방정식 시스템에 대한 정지 상태 부근의 위상 초상화 유형(4.4).

5가지 유형의 평형 상태는 대략적이며, 방정식(4.4)의 우변에서 충분히 작은 변화에도 특성이 변하지 않습니다. 이 경우, 변화는 우변뿐만 아니라 1계 도함수에서도 작아야 합니다. 여섯 번째 평형 상태인 중심은 조잡하지 않습니다. 방정식 오른쪽의 매개변수가 약간 변경되면 안정적이거나 불안정한 초점이 됩니다.

분기 다이어그램

표기법을 소개하겠습니다.

. (4.11)

그런 다음 특성 방정식은 다음과 같은 형식으로 작성할 수 있습니다.

. (4.12)

직교 직교 좌표를 가진 평면을 고려하십시오. 에스 , 디 특성 방정식의 근원의 특성에 의해 결정되는 하나 또는 다른 유형의 평형 상태에 해당하는 영역을 표시하십시오.

.(4.13)

평형 상태의 안정성을 위한 조건은 y의 음의 실수부가 존재하는 것입니다.엘 1 및 엘 2 . 이를 위한 필요충분조건은 불평등의 충족이다.에스 > 0, 디 > 0 . 다이어그램(4.15)에서 이 조건은 매개변수 평면의 1/4에 위치한 점에 해당합니다. 특이점이 초점이 되는 경우엘 1 및 엘 2 복잡한. 이 조건은 다음과 같은 평면의 점에 해당합니다. , 저것들. 포물선의 두 가지 사이의 점에스 2 = 4 디. 반축 포인트 에스 = 0, 디>0, 중심 유형의 평형 상태에 해당합니다. 비슷하게,엘 1 및 엘 2 - 유효하지만 다른 표시, 즉 특이점은 안장이 될 것입니다. 디<0, 등. 결과적으로 매개변수 평면의 파티션 다이어그램을 얻습니다. 에스, 디, 평형 상태의 다른 유형에 해당하는 영역으로.

쌀. 4.10.분기 다이어그램

선형 연립방정식 4.4

선형 시스템의 계수가 a, b, c, d일부 매개변수에 따라 달라지며 이 매개변수가 변경되면 값도 변경됩니다.에스 , 디 . 경계를 통과할 때 위상 초상화의 특성이 질적으로 바뀝니다. 따라서 이러한 경계를 분기 경계라고 합니다. 경계의 반대쪽에는 시스템이 위상적으로 서로 다른 두 가지 위상 초상화와 그에 따라 두 가지 다른 유형의 동작이 있습니다.

다이어그램은 그러한 변화가 어떻게 일어날 수 있는지 보여줍니다. 좌표의 원점인 특수한 경우를 제외하면 안장이 노드에 들어갈 수 있음을 쉽게 알 수 있습니다. y축을 교차할 때 안정적이거나 불안정합니다. 안정적인 노드는 안장이나 안정적인 초점 등으로 이동할 수 있습니다. 안정 노드-안정 초점 및 불안정 노드-불안정 초점 전환은 이 경우 위상 공간의 토폴로지가 변경되지 않기 때문에 분기되지 않습니다. 위상 공간의 토폴로지와 분기 전환에 대한 자세한 내용은 강의 6에서 다루겠습니다.

분기 전환에서 특이점의 안정성 특성이 변경됩니다. 예를 들어 중앙을 통과하는 안정적인 초점은 불안정한 초점으로 바뀔 수 있습니다. 이 분기점은 Andronov-Hopf 분기점그것을 연구한 과학자들의 이름으로. 비선형 시스템에서 이러한 분기로 인해 한계 사이클이 생성되고 시스템이 자체 진동하게 됩니다(강의 8 참조).

예시. 선형 화학 반응 시스템

물질 엑스일정한 속도로 외부에서 유입되어 물질 Y로 변하고 물질의 농도에 비례하는 속도로 변합니다. 와이, 는 반응 영역에서 제거됩니다. 모든 반응은 0차를 갖는 외부로부터 물질의 유입을 제외하고는 1차 반응입니다. 반응 계획은 다음과 같습니다.

(4.14)

방정식 시스템으로 설명됩니다.

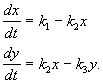(4.15)

우변을 0으로 동일시하여 정상 농도를 얻습니다.

.(4.16)

시스템의 위상 초상화를 고려하십시오. 시스템의 두 번째 방정식(4.16)을 첫 번째 방정식으로 나눕니다. 우리는 다음을 얻습니다.

.(4.17)

방정식(4.17)은 위상 평면에서 변수의 동작을 결정합니다. 이 시스템의 위상 초상화를 구성해 보겠습니다. 먼저 위상 평면에 주요 등각선을 그립니다. 수직 접선의 등각선 방정식:

수평 접선의 등각선에 대한 방정식:

특이점(정지 상태)은 주요 등각선의 교차점에 있습니다.

이제 좌표축이 적분 곡선과 교차하는 각도를 결정합시다.

만약 x= 0, 그럼 .

따라서 적분 곡선에 대한 접선의 기울기의 접선 y=y(x), y축 교차 x=0, 상반면에서 음수입니다(변수 x, y농도 값을 가지므로 위상 평면의 오른쪽 위 사분면에만 관심이 있습니다. 이 경우 접선의 경사각의 접선 값은 원점에서 멀어질수록 증가합니다.

축을 고려 y= 0. 이 축의 교차점에서 적분 곡선은 다음 방정식으로 설명됩니다.

~에 가로축을 가로지르는 적분 곡선의 기울기의 접선은 양수이며 증가함에 따라 0에서 무한대로 증가합니다. 엑스.

에 .

그런 다음 추가 증가와 함께 기울기의 접선은 절대값에서 감소하고 음수를 유지하고 에서 -1 경향이 있습니다. 엑스 ® ¥ . 주 등각선과 좌표축의 적분 곡선에 대한 접선 방향을 알면 위상 궤적의 전체 그림을 쉽게 구성할 수 있습니다.

특이점의 안정성 특성은 Lyapunov 방법을 사용하여 설정됩니다. 시스템의 특성 결정자는 다음과 같은 형식을 갖습니다.

.

행렬식을 확장하면 시스템의 특성 방정식을 얻습니다. , 즉. 특성 방정식의 근은 모두 음수입니다. 따라서 시스템의 정지 상태는 안정 노드입니다. 동시에 물질의 농도 엑스정지 상태가 되는 경향이 항상 단조로우며, 물질 Y의 농도는 최소 또는 최대를 통과할 수 있습니다. 그러한 시스템에서 진동 체제는 불가능합니다.

정의.함수의 특이점을 호출합니다. 외딴, 이 지점의 일부 이웃에 분석 기능이 있는 경우(즉, 링의 분석).

함수의 고립된 특이점 분류는 특이점 근처에서 이 함수의 동작과 관련이 있습니다.

정의.점이라고 한다 일회용의 에서 이 함수의 유한한 한계가 있는 경우 함수의 특이점.

실시예 5함수가 한 점에서 제거 가능한 특이점을 가지고 있음을 보여줍니다.

해결책.첫 번째 놀라운 한계를 회상하면 다음을 계산합니다.

이것은 주어진 함수가 그 지점에서 제거 가능한 특이점을 가진다는 것을 의미합니다.

작업 4.점을 제거할 수 있음을 보여줍니다.

정의.점이라고 한다 폴 함수, 이 함수가 에 대해 무한정 증가하는 경우, 즉 .

분석 함수의 영점과 극점 개념 사이의 연결에 주목합시다. 함수를 로 표현해보자.

점이 함수의 단순 0이면 함수는 단순 극점을 갖습니다.

점이 함수의 차수 0이면 함수의 경우 극점입니다. 주문하다.

실시예 6함수가 한 점에서 3차 극을 가지고 있음을 보여줍니다.

해결책.가정하면 , 우리는 을 얻습니다. 어떤 법칙에 따라 0이 되는 경향이 있으므로 . 그런 다음 기능 자체가 무한정 증가합니다. 따라서 , 즉 특이점은 극점입니다. 함수의 경우 이 점은 분명히 트리플 제로입니다. 따라서 이 함수의 경우 점은 3차 극점입니다.

작업 5.점에 단순 극이 ​​있음을 보여줍니다.

정의.점이라고 한다 본질적으로 특별한 이 지점에서 함수의 유한 또는 무한한 한계가 없는 경우 함수의 지점입니다(함수의 동작이 정의되지 않음).

함수의 필수 특이점이라고 하자. 그런 다음 사전 할당된 복소수에 대해 수렴하는 점 시퀀스가 ​​있으며 값은 다음과 같은 경향이 있습니다. 소초키의 정리).

실시예 7한 점의 함수에 본질적 특이점이 있음을 보여줍니다.

해결책.점 근처에서 주어진 함수의 동작을 고려하십시오. 실제 축의 양의 부분을 따라(즉) 우리는 와 ; 실제 축의 음수 부분(즉)을 따르는 경우 및 . 따라서 에 대한 제한은 없습니다. 정의에 따르면 함수는 한 지점에서 본질적인 특이점을 갖습니다.

Sochocki 정리의 관점에서 0에서 함수의 동작을 고려합시다. 0과 무한대가 아닌 임의의 복소수라고 하자.

평등에서 우리는 . 라고 가정하면 일련의 점을 얻습니다. 확실히, . 이 시퀀스의 각 지점에서 함수는 와 같으므로

작업 6.함수가 한 점에서 본질적 특이점을 가지고 있음을 보여줍니다.

무한대의 점은 항상 함수에 대해 특별한 것으로 간주됩니다.. 이 함수에 원점을 중심으로 하는 원 외부에 다른 특이점이 없는 경우 한 점을 함수의 고립된 특이점이라고 합니다.

고립된 특이점의 분류도 경우로 확장될 수 있습니다.

실시예 8함수가 무한대에서 이중 극을 가지고 있음을 보여줍니다.

해결책.함수를 고려하십시오. 여기서 은 점 부근의 분석 함수이고 입니다. 이것은 함수가 무한대에서 이중 0을 갖지만 함수의 경우 점이 이중 극임을 의미합니다.

실시예 9함수가 무한대에서 본질적 특이점을 갖는다는 것을 보여주십시오.

해결책.유사한 문제가 pr.7에서 고려됩니다. 무한히 먼 점 근처에서 함수의 동작을 고려하십시오. 실제 축의 양수 부분을 따라, 실제 축의 음수 부분을 따라. 이것은 한 점에서 기능의 한계가 없으며 정의에 의해 이 점은 본질적으로 단수임을 의미합니다.

한 지점에서 함수의 특이점 특성은 다음과 같이 판단할 수 있습니다. 주요 부분 이 지점 부근에 로랑 확장.

정리 1.포인트가 되기 위해서는 일회용의 함수의 특이점은 해당 Laurent 전개가 필요하고 충분합니다. 주요 부분을 포함하지 않았습니다.

작업 6.점 근처에서 함수의 테일러 확장을 사용하여 0에서 제거 가능한 특이점이 있음을 보여줍니다.

정리 2.포인트가 되기 위해서는 폴 기능이 필요하고 충분하므로 주요 부분 해당 로랑 확장 제한된 수의 구성원을 포함 :

가장 높은 음수 항의 수가 극의 순서를 결정합니다.

이 경우 함수는 다음과 같이 나타낼 수 있습니다.

여기서 는 점에서 분석 함수이고, 는 극의 차수입니다.

실시예 10함수가 점에 단순 극점을 가지고 있음을 보여줍니다.

해결책.요점을 생각해 봅시다. 예제 2에서 얻은 이 점 근처에서 이 함수의 Laurent 확장을 사용합니다.

이 확장의 주요 부분에서 가장 높은(그리고 유일한) 음의 힘은 1과 같으므로 이 함수의 포인트는 단순 극입니다.

이 결과는 다른 방법으로 얻을 수 있습니다. 형태로 표현하고 넣어 보자 - 이것은 점 및 에서 해석적인 함수이다. 따라서 (8)으로 인해 이 함수는 점에서 단순 극점을 갖습니다.

다른 방법: 점에 단순한 0이 있는 함수를 고려하십시오. 따라서 이 시점에서 간단한 극이 있습니다.

유사하게, 함수를 형식으로 작성하면, 여기서 는 점 및 에 대한 함수 분석입니다. 그러면 점이 함수의 단순 극점이라는 것이 즉시 명확해집니다.

작업 7.함수가 한 점에서 2차의 극점을 갖고 그 점에서 4차의 극점이 있음을 보여주십시오.

정리 3.포인트가 되기 위해서는 본질적으로 특별한 기능의 요점은 다음과 같은 것이 필요하고 충분합니다. 주요 부분 포인트 부근의 로랑 확장 무한한 수의 구성원을 포함 .

예 11.함수의 점에서 특이점의 특성을 결정합니다.

해결책.코사인의 잘 알려진 확장에서 우리는 대신 다음을 넣습니다.

따라서 점 근처에서 Laurent 확장은 다음과 같은 형식을 갖습니다.

여기서 올바른 부분은 하나의 용어입니다. 그리고 주요 부분은 무한한 수의 항을 포함하므로 점은 본질적으로 단수입니다.

작업 8.한 지점에서 함수가 본질적 특이점을 갖는다는 것을 보여주십시오.

몇 가지 기능을 고려하고 해당 지점에서 Laurent 확장을 기록하십시오.

요점이 요점으로 가는 동안 교체해 보겠습니다. 이제 무한대 점의 이웃에서 우리는

새로운 명칭을 도입하는 일만 남았습니다. 우리는 얻는다

여기서 는 주요 부분이고 는 무한히 먼 점 근처에서 함수의 Laurent 확장의 정규 부분입니다. 따라서 점 근처에서 함수의 Laurent 확장에서 주요 부분은 양의 거듭제곱의 급수이고 올바른 부분은 음의 거듭제곱의 급수입니다. 이를 고려하여

그러나 특이점의 성격을 결정하기 위한 위의 기준은 무한히 먼 점에 대해 유효합니다.

예 12.점에서 함수의 특이점의 특성을 찾으십시오. , 그런 다음 어느 시점에서 격리되지 않은 것으로 판명될 수 있습니다.

실시예 15무한히 먼 점에서의 함수는 본질적 특이점을 갖는다. 함수의 점이 고립된 특이점이 아님을 보여줍니다.

해결책.이 함수는 분모의 영점, 즉 점 , 에 무한한 수의 극점을 갖습니다. 이므로 극점이 있는 이웃의 점은 극점의 한계점입니다.

Taylor 급수는 원형 zol에서 해석되는 함수를 연구하기 위한 효과적인 도구 역할을 합니다. 환형 영역에서 해석되는 함수를 연구하기 위해 양의 거듭제곱과 음의 거듭제곱(z - zq)으로 확장을 구성하는 것이 가능하다는 것이 밝혀졌습니다. Taylor 전개를 일반화하는 형태. 두 급수의 합으로 이해되는 급수 (1)을 Laurent 급수라고 합니다. 급수(1)의 수렴영역은 각 급수(2)의 수렴영역의 공통 부분임이 분명하다. 그녀를 찾자. 첫 번째 급수의 수렴영역은 반지름이 Cauchy-Hadamard 공식에 의해 결정되는 원입니다. 수렴원 내부에서 급수 (3)은 해석함수로 수렴하고, 반지름이 작은 원에서는 절대적으로 수렴합니다. 그리고 균일하게. 두 번째 급수는 변수에 대한 거듭제곱 급수입니다. 급수 (5)는 복소수 변수 m-*oo의 해석 함수에 대한 수렴 원 내에서 수렴하고 더 작은 반지름의 모든 원에서는 절대적으로 균일하게 수렴합니다. 이는 급수(4)의 수렴 영역이 원의 모양이라는 것을 의미합니다. - 급수(3)과 (4)의 수렴 공통 영역이 있는 경우 - 급수(1)이 수렴하는 원형 고리 분석 기능에. 또한 모든 링에서 절대적으로 균일하게 수렴합니다. 예제 1. rad Laurent 급수의 수렴 영역 결정 원형 링에서 단일 값이고 비정치적인 격리된 특이점 및 분류(z)는 이 링에서 계수가 Cn은 고유하게 결정되고 공식에 의해 계산됩니다. 여기서 7p는 반지름이 m인 원입니다. 고리 R 내부의 임의의 점 z를 고정합시다. 우리는 반지름이 부등식을 만족하는 점 r0에 중심을 가진 원을 만들고 새로운 고리를 고려합니다.다중 연결 도메인에 대한 코시 적분 정리에 따라 합 (8)의 적분 각각을 개별적으로 변환합시다. 원 7d*를 따라 있는 모든 점 £에 대해 관계 de 균일하게 수렴하는 급수 1 1의 합이 충족됩니다. 따라서 분수 ^는 vi- /"로 나타낼 수 있습니다. / 원의 모든 점 £에 대해 ir> 관계 따라서 분수 ^는 식 (10)과 (12)에서 균일하게 수렴하는 급수의 합으로 나타낼 수 있습니다. 원형 고리의 해석 함수입니다. 따라서 Cauchy의 정리에 따르면 원 7/r 및 7r/이 임의의 원으로 대체되더라도 해당 적분의 값은 변경되지 않습니다. 이를 통해 식 (10)과 (12)를 결합할 수 있습니다.식 (8)의 오른쪽에 있는 적분을 각각 식 (9)와 (11)로 바꾸면 원하는 확장을 얻을 수 있습니다.z는 임의적이므로 고리의 점에서 급수 ( 14)는 이 고리의 모든 곳에서 함수 f(z)로 수렴하고 모든 고리에서 급수는 절대적으로 균일하게 이 함수로 수렴합니다. 이제 형식 (6)의 분해가 고유함을 증명합시다. 한 번 더 분해가 발생한다고 가정하면 고리 R 내부의 모든 곳에서 원주에서 급수 (15)가 균일하게 수렴됩니다. 평등의 양쪽에 곱합니다(여기서 m은 고정 정수이고 두 계열 항을 항으로 통합합니다. 결과적으로 왼쪽에, 오른쪽에 Csh가 표시됩니다. 따라서 (4, \u003d St. m은 임의의 숫자이므로 계수가 공식 (7)에 의해 계산되는 마지막 등식 급수(6)를 고리의 계수에 대한 함수 f(z)의 로랑 급수라고 합니다. 7) Laurent 급수는 일반적으로 복잡한 계산이 필요하기 때문에 실제로 거의 사용되지 않습니다. 일반적으로 가능하면 기본 기능의 기성품 Taylor 확장이 사용됩니다. 확장의 고유성을 기반으로 모든 합법적 인 방법은 동일하게 이어집니다 예 2 Fuiscija /(z)에 두 개의 특이점이 있다고 가정하고 서로 다른 영역의 함수에 대한 Laurent 급수 전개를 고려하십시오. 그리고, 점 r = 0에 중심을 두고 있습니다. 각각에서 함수 f(r)는 해석적입니다. a) 원은 원의 외부입니다(그림 27). 각 영역에서 함수 /(z)의 Laurent 확장을 찾자. /(z)를 기본 분수의 합으로 나타냅니다. a) 원 변환 관계 (16)은 다음과 같습니다. 기하 진행 항의 합에 대한 공식을 사용하여 다음을 얻습니다. b) 함수 -z에 대한 고리는 이 고리에서 수렴 상태를 유지합니다. |z|에 대한 함수 j^j에 대한 급수 (19) 때문입니다. > 1 분기합니다. 따라서 함수 /(z)를 다음과 같이 변환합니다. 공식 (19)를 다시 적용하면 이 급수가 수렴하는 것을 얻습니다. 확장 (18)과 (21)을 관계식 (20)에 대입하면 c) |z|가 있는 함수 -z에 대한 원의 외부성을 얻습니다. > 2 분기 및 함수에 대한 급수 (21) 다음 형식으로 함수 /(z)를 표현해 보겠습니다.<*>공식 (18)과 (19)를 사용하여 OR 1을 얻습니다. 이 예는 동일한 함수 f(z)에 대해 일반적으로 말해서 Laurent 확장이 다른 고리에 대해 다른 형식을 가짐을 보여줍니다. 예 3. 함수 Laurent 시리즈의 8개의 Laurent 급수의 분해를 구합니다. 격리된 특이점과 환형 영역 A에서의 분류 우리는 함수 f(z)의 표현을 다음 형식으로 사용합니다. 두 번째 항을 사용하여 변환 기하 진행의 항의 합에 대한 공식, 우리는 발견된 표현식을 공식 (22)에 대입하면, 우리는 예 4를 얻습니다. 이 확장은 모든 점 z Ф 0에 대해 유효합니다. 이 경우 환형 영역은 하나의 배출 지점 z - 0이 있는 전체 복합 평면입니다. 이 영역은 다음 관계식으로 정의할 수 있습니다. 이 함수는 동일한 추론을 사용하여 Laurent 급수 계수에 대한 공식 (13)에서 영역을 분석합니다. 이전 단락에서와 같이 부등식 Kouiw를 얻을 수 있습니다. 함수 f(z)가 원에 경계가 지정되어 있는 경우(여기서 M은 상수), 고립된 특이점 점 zo는 점의 환형 이웃이 존재하는 경우 함수 f(z)의 고립된 특이점이라고 합니다( 이 집합은 때로 점 2o)의 피어싱된 이웃이라고도 하며, 여기서 f(z) 함수는 단일 값이고 분석적입니다. zo 자체에서 함수는 정의되지 않았거나 단일 값 및 분석적이지 않습니다. 세 가지 유형의 특이점은 점 zo에 접근할 때 함수 /(z)의 동작에 따라 구별됩니다. 고립된 특이점은 다음과 같습니다. 1) 유한한 경우 제거 가능 2) 다음 경우 pmusach 3) 함수 f(z)에 대한 제한이 없는 경우 본질적으로 특이점 정리 16. 함수 f(z)의 고립된 특이점 z0은 점 zo의 이웃에서 함수 f(z)의 로랑 전개가 주요 부분을 포함하지 않는 경우에만 제거 가능한 특이점입니다. 즉, Let zo - 제거 가능한 특이점의 형태를 가집니다. 그런 다음 유한한 것이 존재하므로 함수 f(z)는 점 r의 procological 이웃에 제한됩니다. 우리는 Cauchy 부등식 덕분에 설정합니다. p를 임의로 작게 선택할 수 있으므로 모든 계수는 음수입니다. 거듭제곱(z - 20)은 0과 같습니다. 반대로, 점 zq의 이웃에서 함수 /(r)의 Laurent 확장은 올바른 부분만 포함합니다. 즉, 형식 (23)을 가지므로 따라서 , 테일러입니다. z -* z0에 대해 함수 /(r)에는 한계 값이 있음을 쉽게 알 수 있습니다. 정리 17. 함수 f(z)의 고립된 특이점 zq는 함수 J(z)가 다음과 같은 경우에만 제거 가능합니다. 포인트 zq의 일부 구멍이 뚫린 이웃에 경계, Zgmechai 아닙니다. r0을 f(r)의 제거 가능한 특이점이라고 하자. 함수 f(r)가 점 th를 중심으로 하는 어떤 원에서 분석적이라고 가정합니다. 이것은 포인트의 이름을 정의합니다 - 일회용. 정리 18. 함수 f(z)의 고립된 특이점 zq는 점의 이웃에 있는 함수 f(z)의 Laurent 전개의 주요 부분이 유한(및 양수) 수를 포함하는 경우에만 극점입니다. 0이 아닌 항의, 즉 e. 형식은 4입니다. z0을 극점이라고 합니다. 그 이후로 f(z) 함수가 분석적이며 0이 아닌 점 z0의 구멍이 뚫린 이웃이 존재합니다. 그런 다음 이 이웃에서 분석 함수가 정의되고 따라서 점 zq는 함수의 제거 가능한 특이점(영)이거나 h(z)가 분석 함수이고 h(z0) ∩ 0입니다. 이웃에서 분석적입니다. 이제 함수 f(z)가 점 zo의 구멍이 뚫린 이웃에서 형식 (24)의 분해를 갖는다고 가정합시다. 이것은 이 이웃에서 함수 f(z)가 함수와 함께 분석적임을 의미합니다. 함수 g(z)의 경우, zq가 함수 g(z)의 제거 가능한 특이점이고 존재한다는 것이 분명한 확장이 유효합니다. 그러면 함수는 0 - 함수의 극점에서 경향이 있습니다. 하나 더 간단한 것이 있습니다. 사실. 점 Zq는 함수 g(z) = y가 g(z0) = 0으로 설정하여 점 zq 부근의 분석 함수로 확장될 수 있는 경우에만 함수 f(z)의 극점입니다. 함수 f(z)의 극점을 함수 jfa의 0차라고 합니다. 정리 16과 18은 다음 주장을 의미합니다. 정리 19. 이 점의 구멍이 뚫린 이웃에 있는 Laurent 확장의 주요 부분이 0이 아닌 항을 무한히 많이 포함하는 경우에만 고립된 특이형은 본질적으로 특이합니다. 예제 5. 함수의 특이점은 zo = 0입니다. Laurent 시리즈 격리된 특이점과 분류가 있습니다. 따라서 zo = 0은 제거 가능한 특이점입니다. 영점 부근의 Laurent 급수에서 함수 /(z)의 확장은 올바른 부분만 포함합니다: Example7. f(z) = 함수 f(z)의 특이점은 zq = 0입니다. 실수 축과 허수 축에 대한 이 함수의 동작을 고려하십시오. z -* 0에서 무한한 f(z)는 존재하지 않습니다. 따라서 점 r0 = 0은 함수 f(z)의 본질적으로 특이점입니다. 영점 부근에서 함수 f(z)의 로랑 전개를 찾자. 모든 복잡한 C에 대해 우리는 설정했습니다. 그런 다음 Laurent 확장은 z의 음의 거듭제곱을 가진 무한 수의 항을 포함합니다.

기본 개념 및 정의:

분석 함수 f(z)의 영점은 f(a)=0인 점 "a"입니다.

함수 f(z)의 차수 "n"의 영은 fn(a)¹0인 경우에만 점 "a"입니다.

특이점 "a"는 "a" 이외의 특이점이 없는 이 점의 이웃이 있는 경우 함수 f(z)의 고립된 특이점이라고 합니다.

고립된 특이점에는 세 가지 유형이 있습니다.

제거 가능한 특수 포인트 1개;

3가지 필수 특이점.

특이점의 유형은 발견된 특이점에서 주어진 함수의 거동과 발견된 특이점 근처에서 함수에 대해 얻은 Laurent 급수의 형태를 기반으로 결정할 수 있습니다.

함수의 동작으로 특이점의 유형을 결정합니다.

1. 제거 가능한 특이점.

f(z) 함수의 고립된 특이점 a는 유한한 한계가 있는 경우 제거 가능이라고 합니다.

2. 기둥.

함수 f(z)의 고립된 특이점 a는 다음과 같은 경우 극점이라고 합니다. .

3. 중요한 특이점.

유한도 무한도 존재하지 않는 경우 함수 f(z)의 고립된 특이점 a를 필수 특이점이라고 합니다.

함수의 영점과 극점 사이에 다음 관계가 발생합니다.

점 a가 함수 f(Z)의 차수 n의 극점이 되기 위해서는 이 점이 함수에 대해 차수 n의 0이어야 하는 것이 필요하고 충분합니다.

n=1이면 극을 단순이라고 합니다.

정의:단일 값 문자의 고립된 특이점을 다음과 같이 호출합니다.

a) 분해의 주요 부분이 없는 경우 제거 가능합니다.

b) 주요 부품에 유한한 수의 부재가 포함된 경우 기둥

c) 주요 부분이 무한한 수의 항을 포함하는 경우 본질적으로 특이점.

a) 따라서 제거 가능한 특이점 부근에서 확장은 다음과 같은 형식을 갖습니다.

원 |z-a|의 모든 점에서 함수를 표현합니다.

중심 z=a에서 평등은 거짓입니다. 왜냐하면 z=a에서의 함수는 불연속을 가지며 우변은 연속입니다. 중앙에 있는 함수의 값이 변경되면 오른쪽의 값과 같게 취하면 간격이 제거됩니다. 따라서 이름은 제거할 수 있습니다.

b) 차수가 m인 극 부근에서 Laurent 급수 전개는 다음과 같은 형식을 갖습니다.

c) 단순 기둥 부근

계산을 위한 공제 및 공식.

고립된 특이점 z 0 에서 분석 함수 f(z)의 나머지는 적분 값과 동일한 복소수입니다. , 점 z 0 을 중심으로 하는 원 L을 따라 양의 방향으로 취해지며, 이는 함수 f(z)의 분석 영역(즉, 고리 0에서)에 있습니다.<|z-z0|

고립된 특이점 z 0 에서 함수 f(z)의 나머지는 기호 Res f(z 0) 또는 Res(f(z); z 0)로 표시됩니다. 이런 식으로,

Resf(z0)= . (22.15.1)

공식 (22.15.1)에 n=-1을 넣으면 다음을 얻습니다.

C-1=

또는 Res f(z 0)= C -1 ,

저것들. 특이점 z 0 에 대한 함수 f(z)의 나머지는 Laurent 급수에서 함수 f(z)의 확장에서 음의 지수를 갖는 첫 번째 항의 계수와 같습니다.

공제 계산.

일반 또는 제거 가능한 특이점. 분명히 z=z 0이 함수 f(z)의 정규 또는 제거 가능한 특이점이면 Res f(z 0)=0(이 경우 로랑 분해에 주요 부분이 없으므로 c-1= 0).

폴. 점 z 0 을 함수 f(z)의 단순 극점이라고 합시다. 그런 다음 점 z 0 부근의 함수 f(z)에 대한 Laurent 급수 형식은 다음과 같습니다.

여기에서

따라서 이 동등성을 극한에 z --z 0 으로 전달하면 다음을 얻습니다.

해상도 f(z0)=

본질적으로 특별한 점. 점 z 0 이 함수 f(z)의 본질적으로 특이점인 경우 이 점에서 함수의 나머지를 계산하기 위해 일반적으로 Laurent 급수에서 함수의 확장에서 계수 c-1을 직접 결정합니다.

이벤트 분류. 합계, 이벤트 제품, 해당 속성, 그래픽 표현.

이벤트는 다음과 같이 나뉩니다.

1. 랜덤

2. 믿을 수 있는

3. 불가능

신뢰할 수 있음 - 이것은 반드시 이러한 조건에서 발생하는 이벤트입니다(밤이 지나면 아침이 옴).

무작위는 발생할 수도 있고 발생하지 않을 수도 있는 이벤트입니다(시험 통과).

불가능은 주어진 조건에서 발생하지 않을 이벤트입니다(빨간색 연필만 있는 상자에서 녹색 연필 꺼내기).

허락하다 zq - 함수 f(z)의 특이점, t.s. f(z)그러나 이 시점에서 분석적입니다(특히, 정의되지 않을 수 있음). 포인트 주변에 이런 구멍이 뚫린 부분이 있다면 zq(즉, 집합 O z - zq f(z)는 에일리어틱이고, 그러면 조~라고 불리는 고립된 특이점기능 f(z).이 정의는 경우에도 보존됩니다. zn = oo, 요오드가 점의 구멍이 뚫린 이웃이라면 zq = oo 집합을 이해 z >나 - 원점을 중심으로 하는 어떤 원의 모양. 즉, 특이점 zq는 이 점과 다른 특이점이 있는 이웃이 존재하는 경우 고립되어 있다고 합니다. zq. 아래의 모든 곳에서 단일 값 문자(함수 f(z)고유한 것으로 가정).

함수의 동작에 따라 f(z)~에 z -> zq특이점에는 세 가지 유형이 있습니다. 고립된 특이점 zq 함수 f(z)라고 불리는:

1) 제거 가능한 특이점유한한 한계가 있는 경우

2) 폴한계가 있다면

3) 요점,만약에 f(z)에 대한 유한 또는 무한한 제한이 없습니다. 지-> zq.

예 26.1. 세 가지 유형의 특이점이 모두 실현되었음을 보여줍시다. 고려하다 에프(지)= 포인트 zq = 0은 격리됨

이 기능의 특이점. 식 (22.12)를 사용하여 확장을 얻습니다.

거기에서 lim이 존재한다는 결론이 나온다. 피(z)= 1. 따라서 zq = 0은

기능의 제거 가능한 특이점입니다. fi(z).

기능 f'j(z) =--- 한 지점에 극이 있습니다. 조= 1 때문에

2 아르 자형" 엑스

이제 기능을 고려하십시오. )z(z)= e 1 ^ r 그리고 그것을 보여라 조 = O는 이 함수의 필수 특이점입니다. 노력할 때 지실제 축을 따라 0으로, 함수 f의 왼쪽 및 오른쪽 한계 (지)다른: 림 와 함께 1 / 1 = 0,림 1 /* =운영 체제 이것은 의미합니다,

x->0-0 x->0+0

무엇 f:i(z) 2에 대한 유한도 무한도 없다. -> 오, 즉 zq = 0은 이 함수의 본질적으로 특이점입니다. (요점은 경향이 있으므로 z-iy허수축 기능에서 0으로

제한이 전혀 없습니다.)

물론 고립되지 않은 특이점도 있습니다. 예를 들어. 함수에는 점에 극이 있습니다. z n = -, 피= ±1, ±2,...

따라서, Zq = 0은 이 함수의 고립되지 않은 특이점입니다. 이 점의 임의의 (임의로 작은) 이웃에는 다른 특이점이 있습니다. 지피.

허락하다 조-함수의 최종 고립된 특이점 f(z).그 다음에 f(z)일부 구멍이 뚫린 이웃 0 Zo와 유사합니다. 조이 이웃은 내부 반지름 r = 0인 고리로 간주될 수 있습니다. 정리 25.1에 따르면, 고려 중인 이웃에서 함수 f(z) Laurent 시리즈(25.2)에서 확장할 수 있습니다. 우리는 2에 대한 함수의 동작을 보여줄 것입니다 -> zq (즉, 특이점의 유형 조)분해의 주요 부분의 형태에 따라 다릅니다(25.2). 이 상황은 "주요 부분"이라는 용어의 기원을 설명합니다.

정리 2G.2. 함수 f(z)의 고립된 특이점 zo는 이 점의 구멍이 뚫린 이웃의 Lorap 확장이 oid를 갖는 경우에만 제거할 수 있습니다.

저것들. 올바른 부분으로만 구성, 주요 부분의 모든 계수는 총알과 같습니다.

증거. 1. 하자 조제거 가능한 특이점입니다. 함수의 Laurent 전개를 증명하자. f(z)(26.1) 형식을 가집니다. 특이점부터 조제거 가능하면 유한한 한계가 있습니다. f(z) = 에이.따라서, f(z)일부 구멍이 뚫린 이웃에 경계 0 z - 점의 zq 조,저것들. )(z) 모두 지이 동네에서. 아무거나 가져가 아르 자형. U р /?|를 사용하고 Laurent 급수의 계수에 대해 공식(25.3)을 사용합니다.

확장의 주요 부분의 계수에 대해 n =- 1,-2,... 이러한 값의 경우 피우리는 p~n-e 0에서 아르 자형-> 0. 값 이후 아르 자형임의로 작게 선택할 수 있습니다. 씨~"임의로 작을 수 있습니다. |c t 이후로,| ^^ Mr~n그리고 cn은 p에 의존하지 않습니다. 그러면 cn = 0에 대해 그리고= - 1, -2,..., 증명해야 했던 것.

2. 이제 Laurent 전개가 (26.1) 형식을 갖는다고 가정합시다. 계열(26.1)은 거듭제곱 계열입니다. 따라서 구멍이 뚫린 곳뿐만 아니라 이웃 전체에 수렴됩니다. 지-zq 점을 포함하여 조;그 합계 에스(z)에 대한 분석이다 z 및 S(z) = )(지) 0z에서 - 조아르 자형.따라서 유한한계가 있다. )(지)\u003d Pm 5 (r) \u003d 5 (r) - 따라서 특이점 zq

Z->Zo Z-*Zo

일회용의. 정리가 증명되었습니다.

논평. 제거 가능한 특이점의 구멍이 뚫린 이웃 0 z - zo에서 다음 기능은 정리의 증명에서 따릅니다. f(z)전체 이웃에서 분석되는 함수 S(r)와 일치합니다. 지 - 조 . 따라서 /(th) = S(zq), 그런 다음 함수의 값을 변경하지 않고 f(z)구멍이 뚫린 이웃의 모든 지점에서 우리는 이 함수를 r에서 분석합니다. 기능을 "제거"합니다. 이것은 "제거 가능한 특이점"이라는 용어를 설명합니다. 이러한 점을 함수의 특이점이 아니라 규칙적인 것으로 간주하는 것은 당연합니다. f(z).

예를 들어 기능을 고려하십시오.

예 26.1에서 Pm(n) = 1인 것으로 나타났습니다. 특이점

zq = 0은 제거 가능합니다. /i(0) = 1로 설정하면 특이점을 제거하고 해당 지점에서 분석적인 함수를 얻습니다. zq = 0(그리고 전체 평면 C에서).

이제 Laurent 확장의 관점에서 극을 특성화합시다.

정리 26.3. 함수 f(z)의 고립된 특이점 Zo는 다음과 같은 경우에만 극점입니다., 중심 Zq가 있는 Laurent 전개의 주요 부분이 유한한 수의 고유한 수만 가질 때

n이 있는 0 계수에서:

증거. 1. 하자 zq - 극, 즉 임 /( 지) = 오.

함수의 Laurent 전개를 증명하자. f(z)형태(2G.2)를 갖는다. 임 이후로 f(z)= 오. 지점의 구멍이 뚫린 이웃이 있습니다.

기 zq. 여기서 f(z)분석적이며 0이 없습니다. 그런 다음 기능 지(z) = 1 /f(z)또한 이 구멍이 뚫린 이웃에 대해서도 분석할 것이며, 림 지(z)= 0. 따라서, 조일회용 *-? *0

함수의 특이점 지(z).재정의하자 지(z)그 시점에 조, 퍼팅 지(조)= 0. 그럼 지(z)(천공되지 않은) 지점의 전체 이웃에서 분석이 됩니다. z 0 ,그리고 Z0고립 된 0이 될 것입니다. 로 나타내다 N이 0의 다중도(순서). §23에서와 같이 포인트 부근에서 zq 함수 지(z)형식으로 표현 가능((23.2) 참조)

그리고 (z$) f 0과 y>(z)점의 일부 이웃에서 분석적입니다. 조-왜냐하면 아이피(z)점에서 연속 조그리고 g>(조) F 0" 그럼 아이피(z)이 지점의 일부 이웃에도 0이 없습니다. 따라서 기능 1 /-p(z)도 이 이웃에서 분석적이므로 Taylor 급수에서 확장합니다.

대괄호를 열고 계수 지정을 변경하면 마지막 확장을 형식으로 씁니다.

여기서 c_jv = 1>의 0. 따라서 f(r)의 Laurent 전개의 주요 부분은 유한한 수의 항만 포함합니다. 요구되는 평등(26.2)에 도달했습니다.

2. 구멍이 뚫린 부분에 구멍을 내십시오. 일기능 )(지)는 Laurent 확장(26.2)(더 확장된 형태로, (26.3) 참조)으로 표시되며, 그 주요 부분은 유한 수의 항만 포함하고, 와 함께-디" 에프 0. 우리는 그것을 증명해야 합니다 Zq - 기능 극 f(z).평등(26.3) 곱하기 (G - G o) iV, 우리는 함수를 얻는다

(26.4)의 급수는 구멍이 뚫린 부분뿐만 아니라 점 주변 전체에서 해석 함수로 수렴하는 거듭제곱 급수입니다. Zq. 따라서 기능 h(z)설정하여 th에서 확장하면 이 이웃에서 분석이 됩니다. h(조)= s_dg 에프 0. 그럼

따라서 점 o는 극점이며 정리 26.3이 증명됩니다.

0번째 함수의 다중도(차수) 지(z)= 1//(r)이 호출됩니다 극 주문기능 /(r). 만약 N-극의 차수는 th이고, 지(z)= (r - Zo)Nip(z),그리고 (가) 에프 0이고 정리 26.3 증명의 첫 번째 부분에서 볼 수 있듯이 f(r)의 확장은 (26.3) 형식을 갖습니다. 여기서 c_/v 에프 0. 반대로 f(r)이 급수(26.3)로 확장되고 e-z F 0, 그럼

t.s. N-함수 f(r)의 극점 차수. 이런 식으로, 함수의 zq 극 차수/(G) 점 zq의 구멍이 뚫린 이웃에 있는 Laurent 확장의 주요 부분의 선행하는 0이 아닌 계수의 수와 같습니다.(즉, 그러한 숫자와 동일 N,무슨 s_dg 에프 0과 sp= 0에서 피 > N).

응용 프로그램에 대해 편리한) 다음 주장을 증명합시다.

결론 26.4. 점 zq는 소설의 N차 극점입니다./(G) 만약 그리고 만/(G) 형태로 표현하다

여기서 h(z)는 점 부근의 분석 함수입니다.일 및 h(zo) f 0.

증거. 기능 cp(z) = l/h(z)점 r의 일부 이웃에서 분석적입니다. 추론 26.4의 조건은 다음과 같습니다.

그렇기 때문에 zq - 다중도 제로 N기능 지(z).따라서 다중 극 N기능 /(2).

II 예 26.5. 함수의 고립된 특이점 찾기 그리고 그들의 유형을 결정하십시오.

De u c tio n. (지 2 + 1 )(지+ H) 2 = 0. 만약 지 2 엘- 1 = 0 다음 2 = ±g만약에 (지 4- H) 2 = 0, 그러면 지= -3. 따라서 함수에는 세 개의 특이점이 있습니다. 지= r, 22 = -r, 지3 = - 3. 고려 지:

G - 1차 극(우리는 Corollary 26.4를 사용했습니다). 22 = -나또한 퍼스트 오더의 폴. 2시간 동안:

본질적으로 특이점에 대한 고려로 넘어가겠습니다.

정리 26.6. 함수 f(z)의 고립된 특이점 zq는 zq를 중심으로 하는 Laurent 전개의 주요 부분이 무한히 많이 다른 경우에만 본질적으로 특이점입니다. 0, p가 있는 계수.

증거. 정리 26.6은 정리 26.2 및 26.3에서 바로 이어집니다. 사실 요점이라면 zq는 본질적으로 단수이고, 로랑 전개의 주요 부분은 존재하지 않거나 유한한 수의 항을 포함할 수 없습니다(그렇지 않으면 점 Zq는 제거 가능하거나 기둥이 될 것입니다). 따라서 주요 부분의 항 수는 무한해야 합니다.

반대로, 메인 파트에 무한히 많은 멤버가 포함되어 있으면 Zq는 제거 가능한 점이나 극이 될 수 없습니다. 결과적으로 이 점은 본질적으로 단수입니다.

정의에 따르면, 본질적으로 특이점은 함수 f(2)가 유한하거나 무한한 한계를 갖지 않는다는 사실을 특징으로 합니다. z ->zq. 본질적으로 특이점 근처에서 함수의 동작이 얼마나 불규칙한지에 대한 보다 완전한 아이디어는 다음 정리에 의해 제공됩니다.

정리 26.7(소초키의 정리). zq가 본질적으로 특이값이면 함수 f(z), 그런 다음 임의의 복소수에 대해엘, A = 포함오, z n -> zo 및임 f(zn) = 하지만.

n->os

증거. 경우를 먼저 고려 A =오. 정리 2G.2 증명의 첫 번째 부분에서 우리는 다음과 같이 설정했습니다. f(z)점 r0의 일부 구멍이 뚫린 이웃에 경계가 지정되면 모든 계수 c, n = -주요 부분의 1, - 2,...는 0과 같습니다(따라서 th의 특이점은 제거 가능). 가정에 의해 r0은 본질적으로 특이점이므로, 함수 f(r)는 점 r0의 구멍이 뚫린 이웃에서 제한되지 않습니다. 다음과 같이 좁은 이웃 0 Z를 취합시다. f(지) > 1 (|/(r)| z - zo R/2인 경우 점이 있습니다. 지-2 , 여기서 |/(dd)| > 2 등 : 구멍이 뚫린 이웃 O 71. rn - go 및 lim /(r«) = oo임이 분명합니다. 따라서 A = oo의 경우 정리 26.7

입증되었습니다.

지금 하자 에프오. 먼저 구멍이 뚫린 이웃이 있다고 가정합니다. 0

= -야---- 이 구멍이 뚫린 지역에서 분석을 수행하고 결과적으로

/(G) - 하지만

결과적으로 r은 함수 Φ(r)의 고립된 특이점입니다. 보여줍시다. r0은 본질적으로 Φ(r)의 특이점입니다. 잘못하자. 그러면 유한하거나 무한한 극한 lim Φ(r)이 존재합니다. 왜냐하면

/(r) = A + 이면 Hsh /(r)도 존재하며 이는 조건과 모순됩니다.

에프(지) ~ :-*z 0

정리의 보기. 따라서 r0은 함수 Φ(r)의 본질적으로 특이점입니다. 위에서 증명된 바에 따르면, r n o 및 lim Φ(rn) = oo인 점 rn 의 시퀀스가 ​​있습니다. 여기에서

우리는 f(r) FA점 r의 일부 구멍이 뚫린 이웃에서 이제 이것이 사실이 아니라고 가정합시다. 점의 임의의 작은 구멍이 뚫린 이웃에는 그러한 점이 있습니다. G", f(r") = A. 그렇다면 피구멍이 뚫린 이웃에서 0 f(z u) = L. 따라서 필요한 주장은 참입니다. 피-유오

모든 경우에 정리 26.7이 증명됩니다.

(Sokhotsky's) Theorem 26.7에 따르면, 본질적으로 특이점의 (임의로 작은) 구멍이 뚫린 이웃에서 함수 f(r)은 확장된 복소 평면 C의 임의의 숫자에 임의로 가까운 값을 취합니다.

고립된 특이점을 연구하려면 기본 기본 함수의 잘 알려진 Taylor 확장이 종종 유용합니다.

예 2G.8. 함수에 대한 특이점 zq = 0의 유형 결정

해결 및 e. 테일러 급수의 분자와 분모를 r의 거듭제곱으로 확장합니다. (22.11) 3으로 대체 지 r 대신 1을 빼면

(22.12)를 사용하여 분모의 확장을 얻습니다.

이 확장의 시리즈는 전체 복잡한 평면 €에서 수렴합니다. 우리는

및 /2(2)는 점 부근에서 유사합니다. 조 = 0(그리고 전체 평면에서도) 및 /2(20) 에프 0, 그럼 h(z)또한 점 gF 0의 일부 이웃에서 분석적입니다. 추론 26.4에 따르면 점 조 = 0은 차수의 극점입니다. N = 4.

II 예 26.9. 함수의 특이점 찾기 f(z)= sin j - 유형을 결정하십시오.

P e in e 및 e. 함수는 단일 최종 특이점을 가집니다. zq = 1. C의 다른 지점에서 함수 승 =--- 분석적; 따라서 죄 함수 승분석적일 것이다.

사인(22.12)의 확장으로 대체 - r 대신 다음을 얻습니다.

우리는 점 20 = 1의 구멍이 뚫린 이웃에서 Laurent 급수에서 sin 함수의 확장을 얻었습니다. 결과 확장은 음의 거듭제곱(r - 1)을 갖는 무한히 많은 항을 포함하므로, zq = 1은 필수 특이점입니다(이 경우 Laurent 전개는 주요 부분으로만 구성되며 올바른 부분이 누락됨).

이 경우 급수 확장에 의존하지 않고 정의에서 직접 특이점의 특성을 설정할 수도 있습니다. 실제로, 수렴하는 시퀀스 (r") 및 (2")가 있습니다. 조= 1, 그리고 f(z"n)= 1, /(2") = 0(이러한 시퀀스를 직접 지정). 그래서, f(z)제한이 없을 때 z -> 1 따라서 요점 zq - 1은 본질적으로 단수입니다.

점 근처에서 함수의 Laurent 확장 개념을 소개하겠습니다. Zq = 00이고 이 지점에서 확장과 특이점의 특성 사이의 연결을 고려하십시오. 고립된 특이점과 그 유형(제거 가능한 극점 또는 본질적으로 특이점)의 정의는 다음 사례로 이어집니다. zq = oc 변경되지 않음. 그러나 정리 26.2. 26.3 및 26.6은 Laurent 확장의 특성과 관련하여 변경되어야 합니다. 포인트는 멤버들이 c n (z - 2o) 피. 피= -1,-2,..., 주요 부분, 끝점 근처의 함수의 "불규칙성"을 정의 Zq는 2가 oo인 경향이 있으므로 "정확하게"(0 경향이 있음) 동작합니다. 이에 반해 레귤러 파트의 멤버들은 피= 1,2,... oo 경향이 있습니다; 그들은 특이점의 본질을 결정합니다. Zq = oo. 따라서 oo 주변 확장의 주요 부분은 긍정적 인 힘을 가진 항이 될 것입니다. 피,그리고 정확합니다 - 부정으로.

새로운 변수를 도입하자 승 = 12. 기능 티비= 1/2, u(oo) = 0이 되도록 확장, 일대일 및 이웃을 등각 매핑 z > R포인트들 zq = 00 |w| wq = 0. 함수의 경우 f(z)구멍 뚫린 이웃의 분석 아르 자형 z Zq = oc, 다음 함수 G(w) = f(l/w)노란색 이웃 0 wo = 0에서 분석됩니다. 2 -> oo의 경우 승-> 0, 그럼

그렇기 때문에 지(w)점에 있다 wq = 0은 다음과 같은 유형의 특이점입니다. f(z)그 시점에 Zq = 00. 점 wo = 0의 구멍이 뚫린 이웃에 있는 Laurent 급수의 함수 G(w)를 확장해 보겠습니다.

(26.5)의 오른쪽에 있는 합은 각각 확장의 올바른 부분과 주요 부분을 나타냅니다. 변수로 넘어가자 지,대체 승 = 1/지:

나타내는 피\u003d -A *, 6 * \u003d 6_ " \u003d 피와 함께그리고 그것을 알아차리는 G(l/z) = f(z), 우리는 얻는다

분해(2G.G)는 점 zq의 구멍이 뚫린 이웃에서 함수 f(z)의 Laurent 확장= 오. (2G.6)의 첫 번째 합은 오른쪽 부분, 그리고 두 번째 합계는 주요 부분이 분해. 이 합계는 확장(26.5)의 정확하고 주요 부분에 해당하므로 확장(26.6)은 정리 26.2, 26.3 및 26.6의 유사점을 충족합니다. 따라서 다음 정리는 정리 26.2와 유사합니다.

정리 26.10. 고립된 특이점Zq - 운영 체제 (기능/(G) 이 지점의 구멍이 뚫린 이웃의 Laurent 확장이 다음과 같은 형태를 갖는 경우에만 제거 가능

t.s. 올바른 부분으로만 구성되어 있습니다.

우리는 /(oo) = 공동이웃에 수렴하는 급수(26.7)에 의해 정의된 함수 z > R점 2o \u003d oc, 호출 점 z에서의 해석적오 = 오. (이 정의는 함수의 분석과 동일합니다. 지(w) 그 시점에 워 = 0.)

예 26.11. 함수의 특이점 zq = oo 조사

한계가 유한하기 때문에, 조 = oo는 함수 f(r)의 제거 가능한 특이점입니다. /(oo) = lim J(z)= 0, 그러면 f(z)될 것입니다

틱 앳 포인트 조= 오. 해당 확장(26.7)을 찾는 방법을 보여 드리겠습니다. 변수로 넘어가자 승 = 1 fz.대체 지= 1 /?e, 우리는

(마지막 등식은 점 ww = 0의 구멍이 뚫린 이웃에서 유효하지만 정의를 확장합니다(7(0) = 0). 결과 함수에는 특이점이 있습니다. 승 =±나, 승 =-1/3, 그리고 그 지점에서 Wq = 0은 분석적입니다. 확장 기능 지(w)점차로 승(예 25.7에서와 같이) 그리고 결과 거듭제곱 급수에 대입 w = 1/z함수의 확장(26.7)을 얻을 수 있습니다. f(z).

경우에 대한 정리 26.3 조= oo는 다음 형식으로 다시 작성됩니다.

정리 26.12. 고립된 특이점가다 = OC 함수 f(z)는 Laurent 전개의 주요 부분인 경우에만 극점입니다. (26.6) 유한한 수의 0이 아닌 계수만 가짐와 함께":

여기서 급수는 정규 부분이고 괄호 안의 다항식은 확장의 주요 부분입니다. oc에서 극의 다중도는 극의 다중도로 정의됩니다. wq = 0 함수 지(지).극의 다중도가 숫자와 일치한다는 것을 쉽게 알 수 있습니다. N(26.8)에서.

질문 | (i 2 + 1) (z + 3) 2

작업. 기능을 보여 f(z) =-- -- 에 있다

가리키다 조 =오 폴 오더 3.

필수 특이점에 대한 정리 26.6은 경우에 대해 다시 작성됩니다. 조= os 거의 그대로이며 우리는 그것에 대해 자세히 설명하지 않습니다.