Cum să găsiți puncte singulare izolate. Seria Laurent a izolat puncte singulare și clasificarea lor

Auto

Planul de fază. Portret de fază. Metoda Isoclin. Principalele izocline. Stabilitatea stării staționare. Sisteme liniare. Tipuri de puncte singulare: nod, șa, focus, centru. Exemplu: reactii chimice prima comandă.

Cele mai interesante rezultate privind modelarea calitativă a proprietăților sistemelor biologice au fost obținute folosind modele a două ecuații diferențiale, care permit cercetarea calitativă folosind metoda planul de fază. Să considerăm un sistem de două ecuații diferențiale ordinare autonome vedere generală

(4.1)

P(x,y), Q(x,y)- funcţii continue definite într-un anumit domeniu G plan euclidian ( x,y- coordonate carteziene) şi având în această regiune derivate continue de ordin nu mai mici decât prima.

Regiune G poate fi nelimitat sau limitat. Dacă variabilele x, y au o semnificație biologică specifică (concentrații de substanțe, număr de specii) cel mai adesea zona G reprezintă cadranul pozitiv al semiplanului drept:

0 £ x< ¥ ,0 £ y< ¥ .

Concentrațiile de substanțe sau numărul de specii pot fi, de asemenea, limitate de sus de volumul vasului sau de zona habitatului. Atunci intervalul de variabile are forma:

0 £ x< x 0 , 0 £ y< y 0 .

Variabile x, y schimbare în timp în conformitate cu sistemul de ecuații (4.1), astfel încât fiecare stare a sistemului să corespundă unei perechi de valori variabile ( x, y).

În schimb, fiecare pereche de variabile ( x, y) corespunde unei anumite stări a sistemului.

Luați în considerare un plan cu axe de coordonate pe care sunt trasate valorile variabilelor x,y. Fiecare punct M acest plan corespunde unei anumite stări a sistemului. Acest plan se numește plan de fază și reprezintă totalitatea tuturor stărilor sistemului. Punctul M(x,y) se numește punct reprezentativ sau reprezentativ.

Lasă în momentul inițial de timp t=t 0 coordonatele punctului reprezentativ M 0 (x(t 0), y(t 0)). În fiecare moment următor t punctul reprezentativ se va deplasa în funcție de modificările valorilor variabilelor x(t), y(t). Colectarea punctelor M(x(t), y(t)) pe planul de fază, a cărui poziție corespunde stărilor sistemului în procesul de modificare a variabilelor în timp x(t), y(t) conform ecuațiilor (4.1), se numește traiectoria fazei.

Setul de traiectorii de fază pentru diferite valori inițiale ale variabilelor oferă un „portret” ușor vizibil al sistemului. Constructii portret de fază vă permite să trageți concluzii despre natura modificărilor variabilelor x, y fără cunoașterea soluțiilor analitice ale sistemului original de ecuații(4.1).

Pentru a reprezenta un portret de fază, este necesar să se construiască un câmp vectorial de direcții ale traiectoriilor sistemului în fiecare punct al planului de fază. Setarea incrementuluiD t>0,obținem incrementele corespunzătoare D xŞi D y din expresii:

D x=P(x,y)D t,

D y=Q(x,y)D t.

Direcția vectorială dy/dx la un moment dat ( x, y) depinde de semnul funcţiilor P(x, y), Q(x, y)și poate fi dat de un tabel:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Rezolvarea acestei ecuații y = y(x,c), sau implicit F(x,y)=c, Unde Cu– constantă de integrare, dă familia curbelor integrale din ecuația (4.2) - traiectorii de fază sistem (4.1) pe plan x, y.

Metoda izoclinului

Pentru a construi un portret de fază pe care îl folosesc metoda izoclinului - pe planul de fază sunt trasate linii care intersectează curbele integrale la un unghi specific. Ecuația izoclinului poate fi obținută cu ușurință din (4.2). Să punem

Unde O– o anumită valoare constantă. Sens O reprezintă tangenta unghiului de înclinare a tangentei la traiectoria fazei și poate lua valori din –¥ la + ¥ . Înlocuind în schimb dy/dxîn (4.2) cantitatea O obținem ecuația izoclinului:

.(4.3)

Ecuația (4.3) definește în fiecare punct al planului o tangentă unică la curba integrală corespunzătoare, cu excepția punctului în care P(x,y)= 0, Q (x,y) = 0 , în care direcția tangentei devine incertă, deoarece valoarea derivatei devine incertă:

.

Acest punct este punctul de intersecție al tuturor izoclinelor - punct special.În ea, derivatele temporale ale variabilelor dispar simultan xŞi y.

Astfel, la un punct singular, ratele de modificare a variabilelor sunt zero. În consecință, punctul singular al ecuațiilor diferențiale ale traiectoriilor de fază (4.2) corespunde starea staționară a sistemului(4.1), iar coordonatele sale sunt valorile staționare ale variabilelor x, y.

De un interes deosebit sunt izoclinele principale:

dy/dx=0, P(x,y)=0 – izoclinul tangentelor orizontale și

dy/dx=¥ ,Q(x,y)=0 – izoclinul tangentelor verticale.

Prin construirea izoclinelor principale și găsirea punctului de intersecție a acestora (x,y), ale căror coordonate îndeplinesc condițiile:

vom găsi astfel punctul de intersecție al tuturor izoclinelor planului de fază, în care direcția tangentelor la traiectoriile de fază este incertă. Aceasta - punct singular, care corespunde starea staționară a sistemului(Fig. 4.2).

Sistemul (4.1) are atâtea stări staționare câte puncte de intersecție ale izoclinelor principale sunt pe planul de fază.

Fiecare traiectorie de fază corespunde unui set de mișcări ale unui sistem dinamic, care trec prin aceleași stări și diferă între ele doar la începutul numărării timpului.

Dacă sunt îndeplinite condițiile teoremei lui Cauchy, atunci prin fiecare punct din spațiu x, y, t există o singură curbă integrală. Același lucru este valabil, datorită autonomiei, pentru traiectorii de fază: o singură traiectorie de fază trece prin fiecare punct al planului de fază.

Stabilitate la starea de echilibru

Să fie sistemul într-o stare de echilibru.

Atunci punctul reprezentativ este situat la unul dintre punctele singulare ale sistemului, la care, prin definiție:

.

Dacă un punct singular este sau nu stabil este determinat de dacă punctul reprezentativ pleacă sau nu cu o mică abatere de la starea staționară. În raport cu un sistem de două ecuații, definiția stabilității în limbaje, darata asa.

Starea de echilibru este stabilă dacă pentru orice interval dat de abateri de la starea de echilibru (e )puteți specifica zona d (e ), care inconjoara starea de echilibru si avand proprietatea ca nici o traiectorie care incepe in interiorul regiunii d , nu va ajunge niciodată la graniță e . (Fig. 4.4)

Pentru o clasă mare de sisteme - sisteme brute – natura al cărui comportament nu se schimbă cu o mică modificare a formei ecuațiilor, informații despre tipul de comportament în vecinătatea unei stări staționare pot fi obținute prin examinarea nu a originalului, ci a unui simplificat. liniarizat sistem.

Sisteme liniare.

Luați în considerare un sistem de doi ecuații liniare:

.(4.4)

Aici a, b, c, d- constante, x, y- Coordonate carteziene pe planul de fază.

Vom căuta o soluție generală sub forma:

.(4.5)

Să substituim aceste expresii în (4.4) și să reducem cu e l t:

(4.6)

Sistem algebric de ecuații (4.6) cu necunoscute A, B are o soluție diferită de zero numai dacă determinantul său, compus din coeficienți pentru necunoscute, este egal cu zero:

.

Extinderea acestui determinant, obținem ecuația caracteristică a sistemului:

.(4.7)

Rezolvarea acestei ecuații dă valorile exponentuluil 1,2 , pentru care sunt posibile valori diferite de zero OŞi B soluții pentru ecuația (4.6). Aceste semnificații sunt

.(4.8)

Dacă expresia radicală este negativă, atuncil 1,2 numere complexe conjugate. Să presupunem că ambele rădăcini ale ecuației (4.7) au părți reale diferite de zero și că nu există rădăcini multiple. Atunci soluția generală a sistemului (4.4) poate fi reprezentată ca o combinație liniară de exponențiali cu exponențil 1 , l 2 :

(4.9)

Pentru a analiza natura traiectoriilor posibile ale sistemului pe planul de fază, folosim transformare liniară de coordonate omogene, care va conduce sistemul la forma canonica:

,(4.10)

permiţând o reprezentare mai convenabilă pe planul de fază comparativ cu sistemul original (4.4). Să introducem noi coordonateξ , η dupa formulele:

(4.1)

Din cursul algebrei liniare se știe că în cazul inegalității la zero părțile realel 1 , l 2 sistemul original (4.4) poate fi întotdeauna transformat folosind transformările (4.11) la forma canonică (4.10) și poate fi studiat comportamentul său pe planul de fazăξ , η . Să luăm în considerare diferitele cazuri care se pot prezenta aici.

Rădăcinile λ 1 , λ 2 – valabil și de același semn

În acest caz coeficienții de transformare sunt reali, ne deplasăm din planul realx,yla planul real ξ, η. Împărțind a doua din ecuațiile (4.10) la prima, obținem:

.(4.12)

Integrând această ecuație, găsim:

Unde .(4.13)

Să fim de acord să înțelegem prin λ 2 rădăcina ecuației caracteristice cu un modul mare, care nu încalcă generalitatea raționamentului nostru. Atunci, întrucât în ​​cazul în cauză rădăcinile λ 1 , λ 2 – valabil și de același semn,o>1 , și avem de-a face cu curbe integrale de tip parabolic.

Toate curbele integrale (cu excepția axei η , care corespunde ) atingeți la originea axei ξ, care este și curba integrală a ecuației (4.11). Originea coordonatelor este un punct special.

Să aflăm acum direcția de mișcare a punctului reprezentativ de-a lungul traiectoriilor de fază. Dacă λ 1, λ2 sunt negative, atunci, după cum se vede din ecuațiile (4.10), |ξ|, |η| scade in timp. Punctul reprezentativ se apropie de originea coordonatelor, dar nu o atinge niciodată. În caz contrar, aceasta ar contrazice teorema lui Cauchy, care afirmă că doar o traiectorie de fază trece prin fiecare punct al planului de fază.

Un punct atât de special prin care trec curbele integrale, la fel ca o familie de parabole trece prin origine și se numește nod (Fig. 4.5)

Starea de echilibru a tipului de nod la λ 1, λ2 < 0 este Lyapunov stabil, deoarece punctul reprezentativ se deplasează de-a lungul tuturor curbelor integrale către originea coordonatelor. Acest nod stabil. Dacă λ 1, λ2 > 0, atunci |ξ|, |η| crește în timp și punctul reprezentativ se îndepărtează de originea coordonatelor. În acest caz, punctul special– nod instabil .

Pe planul de fază x, y se va păstra natura calitativă generală a comportării curbelor integrale, dar tangentele la curbele integrale nu vor coincide cu axele de coordonate. Unghiul de înclinare al acestor tangente va fi determinat de raportul coeficienților α , β , γ , δ în ecuaţiile (4.11).

Rădăcinile λ 1 , λ 2 – sunt valabile și de semne diferite.

Convertiți din coordonate x,y la coordonate ξ, η din nou real. Ecuațiile pentru variabilele canonice au din nou forma (4.10), dar acum semnele lui λ 1, λ2 sunt diferite. Ecuația traiectoriilor de fază are forma:

Unde ,(4.14)

Integrând (4.14), găsim

(4.15)

Acest ecuația definește o familie de curbe de tip hiperbolic, unde ambele axe de coordonate– asimptote (la o=1 am avea o familie de hiperbole echilaterale). Axele de coordonate în acest caz sunt, de asemenea, curbe integrale– acestea vor fi singurele curbe integrale care trec prin origine. Fiecaredintre care constă din traiectorii în trei faze: a două mișcări către o stare de echilibru (sau dintr-o stare de echilibru) și dintr-o stare de echilibru. Toate celelalte curbe integrale– sunt hiperbole care nu trec prin origine (Fig. 4.6) Acest punct special se numește "şa ». Liniile de nivel din apropierea unei șei de munte se comportă în mod similar cu traiectoriile de fază din vecinătatea unei șei.

Să luăm în considerare natura mișcării punctului reprezentativ de-a lungul traiectoriilor de fază în apropierea stării de echilibru. Să, de exemplu,λ1 >0, λ2<0 . Apoi punctul reprezentativ plasat pe axă ξ , se va îndepărta de origine și se va plasa pe axă η – se va apropia la infinit de originea coordonatelor, fără a ajunge la el într-un timp finit. Oriunde punctul reprezentativ este în momentul inițial (cu excepția punctului singular și a punctelor de pe asimptotă η =0), se va îndepărta în cele din urmă de echilibru, chiar dacă inițial se va deplasa de-a lungul uneia dintre curbele integrale către un punct singular.

Este evident că un punct singular, cum ar fi o șa, este întotdeauna instabil . Doar în condiții inițiale special selectate la asimptotăη =0 sistemul se va apropia de o stare de echilibru. Totuși, acest lucru nu contrazice afirmația despre instabilitatea sistemului. Dacă socotim, că toate stările inițiale ale sistemului pe planul de fază sunt la fel de probabile, atunci probabilitatea unei astfel de stări inițiale care corespunde mișcării în direcția La punctul singular este egal cu zero. Prin urmare, orice mișcare reală va scoate sistemul din starea de echilibru.Revenind la coordonatex,y,vom obține aceeași imagine calitativă a naturii mișcării traiectoriilor în jurul originii coordonatelor.

Limita dintre cazurile considerate ale unui nod și o șa este cazul Când unul dintre indicatorii caracteristici, de exemplu λ 1 , dispare, ceea ce apare atunci când determinantul sistemului– expresie ad-bc=0(vezi formula 4.8 ). În acest caz, coeficienții părților din dreapta ecuațiilor (4.4) sunt proporționali unul cu celălalt:

iar sistemul are drept stări de echilibru toate punctele dreptei:

Curbele integrale rămase sunt o familie de linii drepte paralele cu un coeficient unghiular , de-a lungul căruia punctele reprezentative fie se apropie de starea de echilibru, fie se îndepărtează de aceasta, în funcție de semnul celei de-a doua rădăcini a ecuației caracteristice λ 2 = a+d.(Fig. 4. 7 ) În acest caz, coordonatele stării de echilibru depind de valoarea inițială a variabilelor.

Rădăcinile λ 1 , λ 2 – complexconjuga

În acest caz, pe bunexŞi y vom au conjugate complexe ξ , η (4.10) . Totuși, prin introducerea unei alte transformări intermediare, este posibil și în acest caz să se reducă considerația la o transformare omogenă liniară reală. Să punem:

(4.16)

Unde a,b,Şi u,v – valori reale. Se poate arăta că transformarea dinx,y La u,v este, în ipotezele noastre, reală, liniară, omogenă cu un determinant diferit de zero. În virtutea ecuaţiilor(4.10, 4.16) avem:

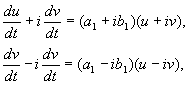
unde

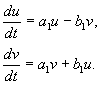(4.17)

Împărțirea celei de-a doua ecuații la prima, obținem:

care este mai ușor de integrat, dacă mergem la sistemul de coordonate polare (r, φ ) . După înlocuire ajungem de unde:

.(4.18)

Astfel, pe planul de fazău, vavem de-a face cu o familie de spirale logaritmice, fiecare dintre ele arepunct asimptotic la origine.Un punct singular, care este punctul asimptotic al tuturor curbelor integrale care au forma de spirale, cuibărit în fiecareprietene, se numește se concentreze ( Fig.4.8 ) .

Să luăm în considerare natura mișcării punctului reprezentativ de-a lungul traiectoriilor de fază. Înmulțirea primei ecuații (4.17) cuu, iar al doilea pe vși adăugând, obținem:

Unde

Lasă o 1 < 0 (o 1 = Reλ ) . Punctul reprezentativ se apropie apoi continuu de originea coordonatelor fără a ajunge la aceasta într-un timp finit. Aceasta înseamnă că traiectoriile de fază sunt spirale răsucitoare și corespund oscilațiilor amortizate variabile. Aceasta - focalizare constantă .

În cazul unui focus stabil, ca și în cazul unui nod stabil, nu numai condiția Lyapunov este îndeplinită, ci și o cerință mai strictă. Și anume, pentru orice abateri inițiale, sistemul se va întoarce, în timp, cât se dorește de poziția de echilibru. O astfel de stabilitate, în care abaterile inițiale nu numai că nu cresc, ci decadează, tinde spre zero, se numește stabilitate absolută .

Dacă în formulă (4.18) o 1 >0 , atunci punctul reprezentativ se îndepărtează de origine și avem de-a face focalizare instabilă . Când se deplasează dintr-un avionu,vla planul de fazăx, yspiralele vor rămâne și ele spirale, dar vor fi deformate.

Să luăm acum în considerare cazul cândo 1 =0 . Traiectorii de fază în avionu, vvor fi cercuri care în avionx,ycorespund elipselor:

Astfel, cânda 1=0 printr-un punct specialx= 0, y= 0 nu trece nicio curbă integrală. Un astfel de punct singular izolat, în apropierea căruia curbele integrale sunt curbe închise, în special, elipse încorporate una în cealaltă și care înglobează punctul singular, se numește centru.

Astfel, sunt posibile șase tipuri de stări de echilibru, în funcție de natura rădăcinilor ecuației caracteristice (4.7). Vedere a traiectoriilor de fază pe un plan x, y pentru aceste șase cazuri este prezentat în Fig. 4.9.

Orez. 4.9.Tipuri de portrete de fază în vecinătatea unei stări staționare pentru un sistem de ecuații liniare (4.4).

Cele cinci tipuri de stări de echilibru sunt brute; caracterul lor nu se modifică cu modificări suficient de mici în părțile din dreapta ale ecuațiilor (4.4). În acest caz, modificările nu numai în partea dreaptă, ci și în derivatele lor de ordinul întâi trebuie să fie mici. A șasea stare de echilibru – centrul – nu este dur. Cu mici modificări ale parametrilor din partea dreaptă a ecuațiilor, acesta devine un focus stabil sau instabil.

Diagrama de bifurcație

Să introducem următoarea notație:

. (4.11)

Atunci ecuația caracteristică se va scrie astfel:

. (4.12)

Să considerăm un plan cu coordonate carteziene dreptunghiulare s , D și marcați pe el zonele corespunzătoare unuia sau altui tip de stare de echilibru, care este determinată de natura rădăcinilor ecuației caracteristice

.(4.13)

Condiția pentru stabilitatea stării de echilibru va fi prezența unei părți reale negative a lui yl 1 și l 2 . O condiție necesară și suficientă pentru aceasta este îndeplinirea inegalitățilors > 0, D > 0 . În diagrama (4.15), această condiție corespunde punctelor situate în primul sfert al planului parametrilor. Un punct singular va fi un focus dacăl 1 și l 2 complex. Această condiție corespunde acelor puncte ale planului pentru care , aceste. puncte dintre două ramuri ale unei paraboles 2 = 4 D. Puncte de osie s = 0, D>0, corespund stărilor de echilibru de tip centru. De asemenea,l 1 și l 2 - sunt valabile, dar de semne diferite, i.e. un punct singular va fi o şa dacă D<0, etc. Ca rezultat, vom obține o diagramă a partiției planului parametrilor s, D, în zone corespunzătoare diferitelor tipuri de stări de echilibru.

Orez. 4.10. Diagrama de bifurcație

pentru un sistem de ecuații liniare 4.4

Dacă coeficienţii sistemului liniar a, b, c, d depinde de un anumit parametru, apoi atunci când acest parametru se schimbă, valorile se vor schimba și eles , D . La trecerea granițelor, caracterul portretului de fază se schimbă calitativ. Prin urmare, astfel de granițe sunt numite granițe de bifurcație - pe părțile opuse ale graniței, sistemul are două portrete de fază topologic diferite și, în consecință, două tipuri diferite de comportament.

Diagrama arată cum pot apărea astfel de schimbări. Dacă excludem cazurile speciale - originea coordonatelor - atunci este ușor de observat că șaua se poate transforma într-un nod, stabil sau instabil la traversarea axei ordonatelor. Un nod stabil poate intra fie într-o șa, fie într-un focar stabil etc. Rețineți că tranzițiile nod stabil - focalizare stabilă și nod instabil - focalizare instabilă nu sunt bifurcații, deoarece topologia spațiului de fază nu se modifică. Vom vorbi mai multe despre topologia spațiului de fază și tranzițiile de bifurcație în Lectura 6.

În timpul tranzițiilor de bifurcație, natura stabilității unui punct singular se schimbă. De exemplu, o focalizare stabilă prin centru se poate transforma într-o focalizare instabilă. Această bifurcație se numește Bifurcația Andronov-Hopf după numele oamenilor de știință care l-au studiat. În timpul acestei bifurcări în sistemele neliniare, se naște un ciclu limită, iar sistemul devine auto-oscilant (vezi Lectura 8).

Exemplu. Sistem de reacție chimică liniară

Substanţă X curge din exterior cu viteza constanta, se transforma in substanta Y si cu viteza proportionala cu concentratia substantei Y, este îndepărtat din sfera de reacție. Toate reacțiile sunt de ordinul întâi, cu excepția influxului de substanță din exterior, care este de ordin zero. Schema de reacție arată astfel:

(4.14)

și este descris de sistemul de ecuații:

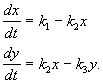(4.15)

Obținem concentrații staționare prin echivalarea părților din dreapta cu zero:

.(4.16)

Să luăm în considerare portretul de fază al sistemului. Să împărțim a doua ecuație a sistemului (4.16) la prima. Primim:

.(4.17)

Ecuația (4.17) determină comportamentul variabilelor pe planul de fază. Să construim un portret de fază al acestui sistem. Mai întâi, să desenăm izoclinele principale pe planul de fază. Ecuația izoclinului tangentelor verticale:

Ecuația izoclinului tangentelor orizontale:

Punctul singular (starea staționară) se află la intersecția izoclinelor principale.

Acum să determinăm în ce unghi se intersectează axele de coordonate cu curbele integrale.

Dacă x= 0, atunci.

Astfel, tangenta tangentei la curbele integrale y=y(x), intersectând axa ordonatelor x=0, este negativă în semiplanul superior (rețineți că variabilele x, y au valori de concentrație și, prin urmare, ne interesează doar cadranul din dreapta sus al planului de fază). În acest caz, tangenta unghiului tangentei crește cu distanța de la origine.

Luați în considerare axa y= 0. În punctul în care această axă intersectează curbele integrale, acestea sunt descrise de ecuație

La tangenta pantei curbelor integrale care traversează axa x este pozitivă și crește de la zero la infinit cu creșterea x.

La .

Apoi, cu o creștere suplimentară, tangenta unghiului de înclinare scade în valoare absolută, rămânând negativă și tinde spre -1 la x ® ¥ . Cunoscând direcția tangentelor la curbele integrale pe izoclinele principale și pe axele de coordonate, este ușor să construiești întreaga imagine a traiectoriilor de fază.

Să stabilim natura stabilității punctului singular folosind metoda Lyapunov. Determinantul caracteristic al sistemului are forma:

.

Extinderea determinantului, obținem ecuația caracteristică a sistemului: , adică Rădăcinile ecuației caracteristice sunt ambele negative. În consecință, starea staționară a sistemului este un nod stabil. În acest caz, concentrația substanței X tinde spre o stare staționară întotdeauna monoton, concentrația substanței Y poate trece prin min sau max. Modurile oscilatorii sunt imposibile într-un astfel de sistem.

Definiţie. Punctul singular al unei funcții se numește izolat, dacă într-o vecinătate a acestui punct este o funcție analitică (adică analitică într-un inel).

Clasificarea punctelor singulare izolate ale unei funcții este legată de comportamentul acestei funcții în vecinătatea punctului singular.

Definiţie. Punctul se numește amovibil punct singular al unei funcţii dacă există o limită finită a acestei funcţii la .

Exemplul 5. Arătați că funcția are o singularitate amovibilă într-un punct.

Soluţie. Amintindu-ne de prima limită remarcabilă, calculăm

Aceasta înseamnă că la un moment dat funcția dată are o singularitate detașabilă.

Sarcina 4. Arătați că punctul este detașabil pentru .

Definiţie. Punctul se numește pol funcție, dacă această funcție crește fără limită la , adică .

Să fim atenți la legătura dintre conceptele de zero și pol ale unei funcții analitice. Să reprezentăm funcția sub forma .

Dacă un punct este un zero simplu al unei funcții, atunci funcția are un pol simplu

Dacă un punct este un zero de ordin pentru o funcție, atunci pentru funcție este un pol comanda .

Exemplul 6. Arătați că funcția are un pol de ordinul trei într-un punct.

Soluţie. Presupunând că obținem. Deoarece avem tendința de a ajunge la zero, după orice lege avem . Apoi, și odată cu ea, funcția în sine crește la nesfârșit. Prin urmare, , adică punctul singular este un pol. Pentru funcție, acest punct este evident triplu zero. Aceasta înseamnă că pentru această funcție punctul este un pol de ordinul trei.

Sarcina 5. Arătați că un punct are un pol simplu.

Definiţie. Punctul se numește semnificativ special punct al unei funcții, dacă în acest punct nu există nici o limită finită, nici infinită a funcției (comportamentul funcției nu este definit).

Fie un punct esențial singular al funcției . Apoi, pentru orice număr complex dat, există o succesiune de puncte care converg către , de-a lungul căreia valorile tind să: ( teorema lui Sokhotsky).

Exemplul 7. Arătați că funcția într-un punct are o caracteristică esențială.

Soluţie. Să luăm în considerare comportamentul funcției date în vecinătatea punctului. Când de-a lungul părții pozitive a axei reale (adică) avem și ; dacă de-a lungul părții negative a axei reale (adică), atunci și . Aceasta înseamnă că nu există limită la . Prin definiție, la un moment dat o funcție are o singularitate esențială.

Să considerăm comportamentul funcției la zero din punctul de vedere al teoremei lui Sokhotsky. Fie orice număr complex diferit de zero și infinit.

Din egalitatea găsim . Presupunând , obținem o succesiune de puncte , . Evident, . În fiecare punct al acestei secvențe funcția este egală cu , prin urmare

Sarcina 6. Arătați că funcția are o singularitate esențială într-un punct.

Punctul de la infinit este întotdeauna considerat special pentru funcție. Un punct se numește punct singular izolat al unei funcții dacă această funcție nu are alte puncte singulare în afara unui anumit cerc centrat la origine.

Clasificarea punctelor singulare izolate poate fi extinsă la caz.

Exemplul 8. Arătați că funcția are un pol dublu la infinit.

Soluţie. Luați în considerare funcția , unde este o funcție analitică într-o vecinătate a punctului și . Aceasta înseamnă că funcția are un zero dublu la infinit, dar atunci pentru funcție punctul este un pol dublu.

Exemplul 9. Arătați că funcția are o singularitate esențială la infinit.

Soluţie. O problemă similară este luată în considerare în Proiectul 7. Să considerăm comportamentul funcției în vecinătatea unui punct la infinit. Când de-a lungul părții pozitive a axei reale și când de-a lungul părții negative a axei reale. Aceasta înseamnă că nu există o limită a funcției într-un punct și, prin definiție, acest punct este în esență special.

Natura singularității unei funcții într-un punct poate fi judecată după parte principală extinderea Laurent în vecinătatea acestui punct.

Teorema 1. Pentru ca punctul să fie amovibil punct singular al funcției, este necesar și suficient ca expansiunea Laurent corespunzătoare nu conținea partea principală.

Sarcina 6. Folosind expansiunea Taylor a unei funcții într-o vecinătate a punctului , arătați că aceasta are o singularitate detașabilă la zero.

Teorema 2. Pentru ca punctul să fie pol funcţia este necesară şi suficientă astfel încât parte principală expansiunea Laurent corespunzătoare conţinea un număr finit de membri :

Numărul celui mai mare termen negativ determină ordinea polului.

În acest caz, funcția poate fi reprezentată ca

unde este o funcție analitică într-un punct, , este ordinea polului.

Exemplul 10. Arătați că funcția are poli simpli în puncte.

Soluţie. Să luăm în considerare ideea. Să folosim expansiunea Laurent a acestei funcții în vecinătatea acestui punct, obținută în Exemplul 2:

Deoarece în partea principală a acestei expansiuni cel mai înalt (și singurul) grad negativ este egal cu unu, atunci punctul este un simplu pol al acestei funcții.

Acest rezultat ar fi putut fi obținut în alt mod. Să o reprezentăm sub forma și să punem - aceasta este o funcție care este analitică la punctul și . Aceasta înseamnă că, în virtutea (8), în punctul această funcție are un pol simplu.

O altă modalitate: luați în considerare o funcție care are un zero simplu într-un punct. Aceasta înseamnă că în acest moment are un stâlp simplu.

În mod similar, dacă scriem funcția sub forma , unde este o funcție analitică în punctul și , atunci este imediat clar că punctul este un simplu pol al funcției .

Sarcina 7. Arătați că funcția are un pol de ordinul 2 în punct și un pol de ordinul 4 în punct.

Teorema 3. Pentru ca punctul să fie semnificativ special punct al funcției, este necesar și suficient ca parte principală Extindere Laurent în vecinătatea punctului conţinea un număr infinit de membri .

Exemplul 11. Determinați natura singularității într-un punct al funcției

Soluţie.În binecunoscuta expansiune cosinus punem în loc de:

Aceasta înseamnă că expansiunea Laurent într-o vecinătate a unui punct are forma

Aici partea corectă este un termen. Și partea principală conține un număr infinit de termeni, deci punctul este în esență special.

Sarcina 8. Arătați că la un moment dat funcția are o singularitate esențială.

Să luăm în considerare o funcție și să scriem expansiunea ei Laurent în punctul:

Să facem o înlocuire, iar punctul merge la obiect. Acum, în vecinătatea punctului de la infinit avem

Rămâne să introducem o nouă denumire. Primim

unde este partea principală și este partea corectă a expansiunii Laurent a funcției în vecinătatea punctului de la infinit. Astfel, în expansiunea Laurent a unei funcții într-o vecinătate a unui punct, partea principală este o serie în puteri pozitive, iar partea corectă este o serie în puteri negative. Ținând cont de acest lucru, înlocuiți

Cu toate acestea, criteriile de mai sus pentru determinarea naturii unei singularități rămân valabile pentru un punct la infinit.

Exemplul 12. Aflați natura singularității funcției la punct. , atunci punctul se poate dovedi a fi neizolat.

Exemplul 15. Funcția într-un punct la infinit are o caracteristică esențială. Arătați că punctul pentru funcție nu este un punct singular izolat.

Soluţie. Funcția are un număr infinit de poli la zerourile numitorului, adică la punctele , . Deoarece , atunci punctul din orice vecinătate a căruia există poli este limita pentru poli.

Seria Taylor servește ca un instrument eficient pentru studierea funcțiilor care sunt analitice într-un cerc zol Pentru a studia funcțiile care sunt analitice într-un domeniu inel, se dovedește a fi posibil să se construiască expansiuni în puteri pozitive și negative (z - zq) de forma care generalizează expansiunile Taylor. Seria (1), înțeleasă ca suma a două serii, se numește seria Laurent. Este clar că regiunea de convergență a seriei (1) este partea comună a regiunilor de convergență ale fiecărei serii (2). Să o găsim. Aria de convergență a primei serii este un cerc a cărui rază este determinată de formula Cauchy-Hadamard În interiorul cercului de convergență, seria (3) converge către o funcție analitică, iar în orice cerc de rază mai mică, converge. absolut și uniform. A doua serie este o serie de puteri în raport cu o variabilă Seria (5) converge în cadrul cercului său de convergență către funcția analitică a unei variabile complexe m-*oo, iar în orice cerc de rază mai mică converge absolut și uniform. înseamnă că aria de convergență a seriei (4) este exteriorul cercului - Dacă atunci există o zonă comună de convergență a seriei (3) și (4) - un inel circular în care seria (1) converge către o funcție analitică. Mai mult, în orice inel, acesta converge absolut și uniform. Exemplul 1. Determinați regiunea de convergență a seriei rad Laurent Puncte singulare izolate și clasificarea lor M Regiunea de convergență a primei serii este exteriorul cercului și regiunea de convergență a celei de-a doua serii este interiorul cercului Astfel, această serie converge în cercuri Teorema 15. Orice funcție f (z), neechivocă și apolitică dintr-un inel circular poate fi reprezentată în acest inel ca suma unei serii convergente, ai cărei coeficienți Cn sunt determinați și calculați în mod unic conform formulelor unde 7p este un cerc cu raza m Să fixăm un punct arbitrar z în interiorul inelului R. Să construim cercuri cu centre în punctul r, ale căror raze satisfac inegalitățile și să considerăm un nou inel Folosind teorema integrală a lui Cauchy pentru o regiune multiplă, avem Transformăm separat fiecare dintre integralele din suma (8). Pentru toate punctele £ de-a lungul cercului 7d* relația de sumă a seriei uniform convergente 1 1 este satisfăcută. Prin urmare, fracția ^ poate fi reprezentată în vi- / "/ Înmulțind ambele părți cu o funcție continuă (O și efectuând. integrarea termen cu termen de-a lungul cercului, obținem că realizăm transformarea integralei a doua într-un mod ușor diferit ca suma unei serii uniform convergente Înmulțind ambele părți cu o funcție continuă) și integrând în termeni de-a lungul cercului 7/, obținem că. Rețineți că integranții din formulele (10) și (12) sunt funcții analitice într-un inel circular. Prin urmare, în virtutea teoremei lui Cauchy, valorile integralelor corespunzătoare nu se vor schimba dacă înlocuim cercurile 7/r și 7r/ cu orice cerc. Acest lucru ne permite să combinăm formulele (10) și (12) Înlocuind integralele din partea dreaptă a formulei (8) cu expresiile lor (9) și respectiv (11), obținem expansiunea necesară punct al inelului, rezultă că seria ( 14) converge către funcția f(z) peste tot în acest inel, iar în orice inel seria converge către această funcție în mod absolut și uniform. Să demonstrăm acum că descompunerea formei (6) este unică. Să presupunem că mai există o expansiune Apoi peste tot în interiorul inelului R vom avea Pe cerc, seria (15) converge uniform. Să înmulțim ambele părți ale egalității (unde m este un întreg fix și să integrăm ambele serii termen cu termen. Ca rezultat, obținem în partea stângă, iar în dreapta - Sch. Astfel, (4, = St. Deoarece m este un număr arbitrar, ultima egalitate demonstrează unicitatea seriei (6), ai cărei coeficienți sunt calculați folosind formulele (7), se numește seria Laurent a funcției f(z) din inel setul de termeni ai acestei serii cu puteri nenegative se numește partea corectă a seriei Laurent, iar cu cei negativi - partea sa principală Formulele (. 7) pentru coeficienții seriei Laurent sunt rar utilizate în practică, deoarece, ca un de regulă, acestea necesită calcule greoaie de funcţii din diverse regiuni, presupunând că f(r) are două puncte singulare: De aceea, există trei regiuni inelare, cu centrul în punctul r = 0. în fiecare dintre ele funcţia /(r) este analitică: a. ) inel cerc exteriorul cercului (Fig. 27). Să găsim expansiunile Laurent ale funcției /(z) în fiecare dintre aceste regiuni. Reprezentăm /(z) ca o sumă de fracții elementare a) Cercul Transformăm relația (16) după cum urmează. Înlocuim expansiunile găsite în formula (17). : Această expansiune este seria Taylor a funcției /(z). b) Inelul pentru funcția -r rămâne convergent în acest inel, deoarece Seria (19) pentru funcția j^j pentru |z| > 1 diverge. Prin urmare, transformăm funcția /(z) astfel: aplicând din nou formula (19), obținem că Această serie converge pentru. Înlocuind expansiunile (18) și (21) în relația (20), obținem c) Exteriorul cercului pentru funcția -z pentru |z| > 2 diverge, iar seria (21) pentru func- Reprezentăm funcția /(z) în următoarea formă: /<*>Folosind formulele (18) și (19), obținem OR 1 Acest exemplu arată că pentru aceeași funcție f(z) expansiunea Laurent, în general, are o formă diferită pentru diferite inele. Exemplul 3. Aflați expansiunea celei de-a 8-a serii Laurent a unei funcții Serie Laurent Puncte singulare izolate și clasificarea lor într-un domeniu inel A Folosim reprezentarea funcției f(z) în următoarea formă: și transformăm al doilea termen Folosind formula pentru suma termenilor unei progresii geometrice, obținem Înlocuind expresiile găsite în formula (22), avem Exemplul 4. Extindeți funcția din seria Laurent în punctul zq = 0. Pentru orice complex avem Put This expansiunea este valabilă pentru orice punct z Ф 0. În în acest caz, regiunea inelară reprezintă întregul plan complex cu un punct aruncat z - 0. Această regiune poate fi definită prin următoarea relație: Această funcție este analitică în regiunea Din formulele (13) pentru coeficienții seriei Laurent, folosind aceeași raționând ca în paragraful anterior, se pot obține inegalitățile Kouiw. dacă funcția f(z) este mărginită pe un cerc, unde M este o constantă), atunci Puncte singulare izolate Punctul zo se numește punct singular izolat al funcției f(z) dacă există o vecinătate inelă a punctului ( această mulțime se numește uneori o vecinătate perforată a punctului 2o), în care funcția f(z) este unică și analitică. În punctul zo însuși, funcția este fie nedefinită, fie lipsită de ambiguitate și analitică. În funcție de comportamentul funcției /(r) la apropierea punctului zo se disting trei tipuri de puncte singulare. Un punct singular izolat se spune a fi: 1) detașabil dacă există un finit 2) pymusach dacă 3) un punct esențial singular dacă funcția f(z) nu are limită la Tipul unui punct singular izolat este strâns legat de natura expansiunii Laurent a functiei prin centrul perforat al . Teorema 16. Un punct singular izolat z0 al unei funcții f(z) este un punct singular detașabil dacă și numai dacă expansiunea Laurent a funcției f(z) într-o vecinătate a punctului zo nu conține o parte principală, adică, are forma Fie zo detașabil punct singular. Atunci există un finit, prin urmare, funcția f(z) este mărginită într-o vecinătate procologică a punctului z. Punem în virtutea inegalităților lui Cauchy Deoarece p poate fi ales arbitrar mic, atunci toți coeficienții la puteri negative (z. - 20) sunt egale cu zero: În schimb, fie Laurent extinderea funcției /(r) într-o vecinătate a punctului zq conține doar partea corectă, adică are forma (23) și, prin urmare, este Taylor. Este ușor de observat că pentru z -* z0 funcția /(z) are o valoare limită: Teorema 17. Un punct singular izolat zq al funcției f(z) este detașabil dacă și numai dacă funcția J(z) este delimitat într-o vecinătate perforată a punctului zq, Zgmechai nu. Fie r un punct singular detașabil al funcției /(r). Presupunând că funcția /(r) este analitică într-un cerc cu centrul în punctul r. Aceasta determină numele punctului - detașabil. e. are forma 4 Fie z0 un pol. De atunci există o vecinătate perforată a punctului z0 în care funcția f(z) este analitică și diferită de zero. Atunci în această vecinătate este definită o funcție analitică și Prin urmare, punctul zq este un punct singular detașabil (zero) al funcției sau unde h(z) este o funcție analitică, h(z0) Φ 0. Atunci h(zo) Φ 0 este și analitică, atunci funcția φ este analitică într-o vecinătate a punctului zq și, prin urmare, de unde obținem că Să presupunem acum că funcția f(z) are o expansiune a formei (24) într-o vecinătate perforată de punctul zо. Aceasta înseamnă că în această vecinătate funcția f(z) este analitică împreună cu funcția. Pentru funcția g(z) expansiunea este valabilă, din care se poate observa că zq este un punct singular detașabil al funcției g(z) și există atunci funcția la 0 tinde să fie polul funcției este un alt fapt simplu. Punctul Zq este un pol al funcției f(z) dacă și numai dacă funcția g(z) = yj poate fi extinsă la o funcție analitică în vecinătatea punctului zq prin stabilirea g(z0) = 0. Ordinea al polului funcţiei f(z) se numeşte ordinul zero al funcţiei jfa. Următoarea afirmație decurge din teoremele 16 și 18. Teorema 19. Un punct singular izolat este în esență singular dacă și numai dacă partea principală a expansiunii Laurent într-o vecinătate perforată a acestui punct conține infiniti de termeni nenuli. Exemplul 5. Punctul singular al funcției este zo = 0. Avem Seria Laurent Puncte singulare izolate și clasificarea lor Prin urmare, zo = O este un punct singular amovibil. Extinderea funcției /(z) într-o serie Laurent în vecinătatea punctului zero conține doar partea corectă: Exemplul7. /(z) = Punctul singular al funcției f(z) este zq = 0. Să considerăm comportamentul acestei funcție pe axele reale și imaginare: pe axa reală la x 0, pe axa imaginară În consecință, există nu este nici o limită finită, nici infinită pentru f(z) la z -* 0 nu există. Aceasta înseamnă că punctul r = 0 este un punct esențial singular al funcției f(z). Să găsim expansiunea Laurent a funcției f(z) în vecinătatea punctului zero. Pentru orice complex C avem Set. Atunci expansiunea Laurent conține un număr infinit de termeni cu puteri negative ale lui z.

Concepte de bază și definiții:

Zero al funcției analitice f(z) este punctul „a” pentru care f(a)=0.

Un zero de ordinul „n” al unei funcții f(z) este un punct „a” dacă fn(a)¹0.

Un punct singular „a” se numește punct singular izolat al unei funcții f(z) dacă există o vecinătate a acestui punct în care nu există alte puncte singulare decât „a”.

Există trei tipuri de puncte singulare izolate: .

1 puncte singulare detașabile;

3 puncte esențial singulare.

Tipul punctului singular poate fi determinat pe baza comportamentului unei funcții date la punctul singular găsit, precum și din forma seriei Laurent obținută pentru funcția din vecinătatea punctului singular găsit.

Determinarea tipului unui punct singular prin comportamentul funcției la acesta.

1. Puncte singulare detașabile.

Un punct singular izolat a al unei funcții f(z) se numește amovibil dacă există o limită finită.

2.Stalpi.

Un punct singular izolat a al unei funcții f(z) se numește pol dacă .

3. Puncte în esență singulare.

Un punct singular izolat a al unei funcții f(z) se numește punct esențial singular dacă nu există nici finit, nici infinit.

Următoarea relație există între zerourile și polii funcției.

Pentru ca punctul a să fie un pol de ordinul n al funcției f(Z), este necesar și suficient ca acest punct să fie un zero de ordinul n pentru funcția .

Dacă n=1 polul se numește simplu.

Definiţie: Un punct singular izolat de natură lipsită de ambiguitate se numește:

a) detașabil dacă lipsește partea principală a descompunerii;

b) un pol, dacă partea principală conține un număr finit de termeni;

c) un punct esenţial singular dacă partea principală conţine un număr infinit de termeni.

a) Astfel, în vecinătatea unui punct singular amovibil, expansiunea are forma:

exprimă funcția în toate punctele cercului |z-a|

La centrul z=a egalitatea nu este adevărată, deoarece funcția la z=a are o discontinuitate, iar partea dreaptă este continuă. Dacă se modifică valoarea funcției din centru, luând-o egală cu valoarea din dreapta, atunci decalajul va fi eliminat - de unde și numele - detașabil.

b) În vecinătatea unui pol de ordinul m, expansiunea seriei Laurent are forma:

c) În vecinătatea unui stâlp simplu

Deduceri și formule de calcul.

Reziduul unei funcții analitice f(z) la un punct singular izolat z 0 este un număr complex egal cu valoarea integralei , luată în direcția pozitivă de-a lungul cercului L cu centrul în punctul z 0 situat în domeniul analiticității funcției f(z) (adică în inelul 0<|z-z0|

Restul funcției f(z) la un punct singular izolat z 0 este notat cu simbolul Res f(z 0) sau Res (f(z); z 0). Astfel,

Res f(z 0)= . (22.15.1)

Dacă punem n=-1 în formula (22.15.1), obținem:

C -1 =

sau Res f(z 0)= C-1,

aceste. restul funcției f(z) față de punctul singular z 0 este egal cu coeficientul primului termen cu exponent negativ în expansiunea funcției f(z) din seria Laurent.

Calculul deducerilor.

Puncte singulare regulate sau amovibile. Evident, dacă z=z 0 este un punct singular regulat sau detașabil al funcției f(z), atunci Res f(z 0)=0 (expansiunea Laurent în aceste cazuri îi lipsește partea principală, deci c-1=0) .

Pol. Fie punctul z 0 un pol simplu al funcției f(z). Atunci seria Laurent pentru funcția f(z) în vecinătatea punctului z 0 are forma:

De aici

Prin urmare, trecând în această egalitate la limita la z --z 0, obținem

Res f(z0)=

Punct în esență special. Dacă punctul z 0 este un punct esențial singular al funcției f(z), atunci pentru a calcula reziduul funcției în acest punct, coeficientul c-1 în extinderea seriei Laurent a funcției este de obicei determinat direct.

Clasificarea evenimentelor. Suma, produsul evenimentelor, proprietățile acestora, reprezentarea grafică.

Evenimentele sunt împărțite în:

1. Aleatoriu

2. De încredere

3. Imposibil

Fiabil este un eveniment care are loc neapărat în condiții date (noaptea urmează dimineața).

Un eveniment aleatoriu este un eveniment care se poate întâmpla sau nu (procesarea unui examen).

Un eveniment imposibil este un eveniment care nu va avea loc în condiții date (scoaterea unui creion verde dintr-o cutie doar cu cele roșii).

Lasă zq este punctul singular al funcției /(r), t.s. f(z) dar este analitic în acest moment (în special, este posibil să nu fie definit la acesta). Dacă există o astfel de vecinătate perforată a punctului zq (adică mulțimea O z - zq f(z) este aialitic, atunci zo numit punct singular izolat funcții f(z). Această definiție rămâne aceeași în cazul zn = oo, dacă iodul este străpuns de vecinătatea punctului zq = oo înțelege set z> eu - exteriorul unui cerc cu centrul la origine. Cu alte cuvinte, un punct special Se spune că zq este izolat dacă există o vecinătate a acestui punct în care este vorba de alte puncte singulare, altele decât zq. În cele ce urmează, considerăm doar puncte singulare cu un caracter unic (funcția f(z) presupus a fi lipsit de ambiguitate).

În funcţie de comportamentul funcţiei f(z) la z -> zq Există trei tipuri de puncte singulare. Punct singular izolat funcții zq f(z) numit:

1) punct singular detașabil, dacă există o limită finită

2) pol, dacă există o limită

3) în esență un punct special, Dacă f(z) nu are nici o limită finită, nici infinită la z-> zq.

Exemplul 26.1. Să arătăm că toate cele trei tipuri de puncte singulare sunt realizate. Să luăm în considerare f(z)= Punct zq = 0 este izolat

punct special al acestei funcții. Folosind formula (22.12), obținem expansiunea

din care rezultă că există lim fi(z)= 1. Prin urmare zq = 0 este

este un punct singular detașabil al funcției fi(z).

Funcţie f‘j(z) =---are un stâlp într-un punct zo= 1 deoarece

2 r„X

Să luăm acum în considerare funcția )з(z)= e 1 ^ r și arătați că zo = O este un punct esențial singular al acestei funcții. Când te străduiești z la zero de-a lungul axei reale limitele stânga și dreapta ale funcției /z (z) diferit: lim Cu 1 / 1 = 0, lim s 1 /* = os. De aici rezultă,

x->0-0 x->0+O

Ce f:i(z) nu are limită nici finită, nici infinită la 2 -> Oh, asta este. zq = O este un punct esenţial singular al acestei funcţii. (Rețineți că așa cum tinde punctul z - iy la zero de-a lungul funcției axei imaginare

nu are nicio limită.)

Există, desigur, puncte singulare neizolate. De exemplu. funcția are poli în puncte z n = -, n= ±1, ±2,...

Prin urmare, Zq = 0 este un punct singular neizolat al acestei funcții: în orice vecinătate (oricât de mică) a acestui punct există alte puncte singulare g p.

Lasă zo- punct singular izolat finit al unei funcții f(z). Apoi f(z) este similară într-o zonă perforată a punctului 0 Zo zo această vecinătate poate fi considerată ca un inel cu raza internă r = 0. Prin teorema 25.1, în vecinătatea luată în considerare funcția f(z) poate fi extins într-o serie Laurent (25.2). Vom arăta că comportamentul funcției la 2 -> zq (adică tipul punctului singular zo) depinde de tipul părții principale a expansiunii (25.2); Această împrejurare explică originea termenului „partea principală”.

Teorema 2G.2. Un punct singular izolat zo al unei funcții f(z) este detașabil dacă și numai dacă expansiunea Loap într-o vecinătate perforată a acestui punct are oid

aceste. constă doar din partea corectă, iar toți coeficienții părții principale sunt egali cu glonțul.

Dovada. 1. Lasă zo- punct singular amovibil. Să demonstrăm că expansiunea Laurent a funcției f(z) are forma (26.1). De la punctul special zo detașabil, atunci există o limită limită finită f(z) = A. Prin urmare, f(z) este mărginită într-o vecinătate perforată a punctului 0 z - zq zo, aceste. )(z) pentru toată lumea z din această vecinătate. Să luăm oricare r. U р /?| și folosiți formulele (25.3) pentru coeficienții seriei Laurent:

Pentru coeficienții părții principale a expansiunii n =- 1,-2,... Pentru astfel de valori n avem p~ p-e 0 la r-> 0. Deoarece valoarea r poate fi ales arbitrar mic, atunci domnule~" poate fi cât se dorește. Din moment ce |s t,| ^ Mr~p iar c„ nu depind de p, atunci c„ = 0 at Şi= - 1, -2,..., care este ceea ce trebuia dovedit.

2. Să presupunem acum că expansiunea Laurent are forma (26.1). Seria (26.1) este o serie de puteri și. prin urmare, converge nu numai în zona perforată, ci și în toată vecinătatea z-zq inclusiv punctul zo; suma acestuia S(z) este analitic la z și S(z) = )(z) la 0 z - zo R. Prin urmare, există o limită limită finită )(z)= Pt 5(g) = 5(th) - Prin urmare, punctul singular zq

Z->Zo Z-*Zo

amovibil. Teorema a fost demonstrată.

Comentariu. Din demonstrarea teoremei rezultă că într-o vecinătate perforată 0 z - zo a unui punct singular detașabil funcția f(z) coincide cu funcția 5(r), care este analitică în întreaga vecinătate z - zo. Prin urmare, dacă stabilim /(th) = S(zq), apoi, fără a modifica valorile funcției f(z)în orice punct al cartierului perforat, vom face această funcție analitică în Go, i.e. Să „eliminăm” caracteristica. Aceasta explică termenul „funcție detașabilă”. Este firesc să considerăm astfel de puncte ca fiind puncte regulate și nu singulare ale funcției f(z).

Luați în considerare, de exemplu, funcția

În exemplul 26.1 s-a arătat că Pm Nr) = 1. adică. punct singular

zq = 0 detașabil. Setând /i(0) = 1, eliminăm astfel singularitatea și obținem o funcție care este analitică în punctul zq = 0 (și în tot planul C).

Să caracterizăm acum polii în termeni de expansiuni Laurent.

Teorema 26.3. Un punct singular izolat Zo al unei funcții f(z) este un pol dacă și numai dacă, când partea principală a expansiunii Laurent cu centrul Zq are doar un număr finit de distincte

de la zero coeficienți cu n:

Dovada. 1. Lasă zq - pol, i.e. lim/( z) = oo.

Să demonstrăm că expansiunea Laurent a funcției f(z) are forma (2G.2). Din moment ce lim f(z)= oo. apoi există o vecinătate perforată a punctului

ki zq. în care f(z) este analitic și nu are zerouri. Apoi funcția g(z) = 1 /f(z) va fi, de asemenea, analitic în acest cartier perforat, și lim g(z)= 0. Prin urmare, Zo este detașabil *-? *0

punct singular al funcției g(z). Să definim g(z) la punct zo, punând g(zo)= 0. Apoi g(z) va deveni analitic în întreaga vecinătate a punctului (nu străpuns). z 0 ,şi z 0 va fi zeroul său izolat. Să notăm prin N multiplicitatea (ordinea) acestui zero. După cum sa arătat în §23, în vecinătatea punctului funcția zq g(z) poate fi reprezentat sub forma (vezi (23.2))

şi (z$) f 0 și y>(z) este analitic într-o anumită vecinătate a punctului zo- Deoarece ip(z) continuu la un punct zoŞi g>(zo) Ф 0" atunci ip(z) nu are zerouri în vreo vecinătate a acestui punct. Prin urmare, funcția 1 /-p(z) va fi, de asemenea, analitic în acest cartier și, prin urmare, se extinde în el într-o serie Taylor:

Deschizând parantezele și schimbând denumirile coeficienților, scriem ultima expansiune sub forma

unde c_jv = 1>o f 0. Astfel, partea principală a expansiunii Laurent a funcției /(r) conține doar un număr finit de termeni; am ajuns la egalitatea dorită (26.2).

2. Lăsați în vecinătatea perforată a punctelor th funcţie )(z) este reprezentată de expansiunea Laurent (26.2) (pentru o formă mai detaliată, vezi (26.3)), a cărei parte principală conține doar un număr finit de termeni și Cu- d" f 0. Este necesar să se demonstreze că Zq - pol de funcție f(z).Înmulțirea egalității (26.3) cu (G - G o) iV , obținem funcția

Seria din (26.4) este o serie de puteri care converge către o funcție analitică nu numai în punctul perforat, ci și în întreaga vecinătate a punctului. Zq. Prin urmare funcția h(z) va deveni analitic în acest cartier dacă îl definim în continuare prin punerea h(zo)= s_dg f 0. Apoi

Astfel, punctul th este un pol, iar teorema 26.3 este demonstrată.

Multiplicitatea (ordinea) funcției zero g(z)= 1//(g) se numește ordinea polului a-a funcție /(r). Dacă N- ordinea polului lui, atunci g(z)= (g - Zo) N ip(z),și (du-te) F 0 și, așa cum se arată în prima parte a demonstrației teoremei 26.3, expansiunea funcției /(r) are forma (26.3), unde c_/v f 0. În schimb, dacă /(r) este extins în seria (26.3) și e-i F 0, atunci

c.t. N- ordinea polului funcţiei /(r). Astfel, ordinea polilor a funcției zq/(G) este egal cu numărul celui mai mare coeficient diferit de zero al părții principale a expansiunii Laurent în vecinătatea perforată a punctului zq(adică egal cu acest număr N, ce s_dg f 0 și Sp= 0 la n > N).

Să demonstrăm următoarea afirmație, care este convenabilă pentru aplicații.

Corolarul 26.4. Punctul zq este un pol de ordinul N al ficțiunii/(G) atunci și numai când/(G) reprezentabil în formă

unde h(z) este o funcție analitică în vecinătatea punctului th și h(zo) f 0.

Dovada. Funcţie cp(z) = l/h(z) este analitică în apropierea punctului h. Condiția Corolarului 26.4 este echivalentă cu următoarea:

De aceea zq - multiplicitate zero N funcții g(z).şi deci polul multiplicităţii N funcții /(2).

II Exemplul 26.5. Găsiți puncte singulare izolate ale unei funcții și determinați tipul lor.

Rezolvare: Punctele în care (z 2 + 1 )(z+ Z) 2 = 0. Dacă z 2 L- 1 = 0, apoi 2 = ±g Dacă (z 4- 3) 2 = 0, atunci z= -3. Prin urmare, funcția are trei puncte singulare z= g, 22 = -g, Z3 = - 3. Luați în considerare z:

G - stâlp de ordinul întâi (am folosit Corolarul 26.4). Se poate dovedi într-un mod similar că 22 = -i tot un stâlp de ordinul întâi. Pentru 2z avem:

Să trecem la considerarea punctelor esențial singulare.

Teorema 26.6. Un punct singular izolat zq al unei funcții f(z) este esențial singular dacă și numai dacă partea principală a expansiunii Laurent cu centrul zq are infinit de multe distincte de. zero, coeficienți de la p.

Dovada. Teorema 26.6 rezultă direct din teoremele 26.2 și 26.3. Într-adevăr, dacă punctul zq este în esență specială, atunci partea principală a expansiunii Laurent nu poate fi absentă sau nu poate conține un număr finit de termeni (altfel punctul Zq va fi fie detașabil, fie un stâlp). Prin urmare, numărul de termeni din partea principală trebuie să fie infinit.

În schimb, dacă partea principală conține infiniti de termeni, atunci Zq nu poate fi nici un punct detașabil, nici un stâlp. Rezultă că acest punct este în esență special.

Conform definiției, un punct esențial singular se caracterizează prin faptul că funcția /(2) nu are limită nici finită, nici infinită pentru z ->zq. O idee mai completă despre cât de neregulat este comportamentul unei funcții în vecinătatea unui punct esențial singular este dată de următoarea teoremă.

Teorema 26.7 (teorema lui Sokhotsky). Dacă zq este esențial pentru persoane, punctul funcției f(z), apoi pentru orice număr complex L, inclusiv A = Oh, există o succesiune de puncte z n astfel încât z n -> zo şi lim f(zn) = O.

p->os

Dovada. Să luăm în considerare mai întâi cazul A = oo. În prima parte a demonstrației teoremei 2G.2 am stabilit că dacă f(z) este mărginită într-o vecinătate perforată a punctului r, apoi toți coeficienții c", n = - 1,- 2,... din partea principală sunt egale cu zero (și, prin urmare, singularitatea din go este detașabilă). Deoarece prin condiția th este un punct singular esențial, atunci în orice vecinătate perforată a punctului th funcția f(r) este nemărginită. Să luăm un cartier puternic 0 Z astfel încât f(zi) > 1 (dacă |/(r)| z - zo I/2 există un punct z-2 , în care |/(yy)| > 2 etc.: în cartierul perforat O 71. Este evident că r„ -e go și lim /(r“) = oo. Astfel, în cazul A = oo, Teorema 26.7

dovedit.

Lasă-l acum A f oo. Să presupunem mai întâi că există o vecinătate perforată 0

= -aa---- va fi analitic în acest cartier perforat și, în consecință,

/(G) - O

În consecință, go este un punct singular izolat al funcției Φ(r). Vă vom arăta. că r este un punct esenţial singular al lui Φ(r). Acest lucru poate să nu fie adevărat. Atunci există o limită lim Ф(r), finită sau infinită. Pentru o vreme

/(r) = A + , atunci există și Hsh /(r), care contrazice condiția

F(g) ~ :-*z 0

Văd teorema. Astfel, r0 este un punct esenţial singular al funcţiei Φ(r). Conform celor dovedite mai sus, există o succesiune de puncte r n astfel încât r n-th și lim Ф(r n) = oo. De aici

Am demonstrat afirmația cerută sub ipoteza că /(r) F Aîntr-o vecinătate perforată a punctului go- Să presupunem acum că acest lucru este fals, adică. în orice vecinătate perforată arbitrar mică a punctului th există un astfel de punct G", că /(r") = L. Atunci pentru orice nîn vecinătatea perforată 0 f(z u) = А Astfel, afirmația dorită este adevărată n-iuo

în toate cazurile, iar teorema 26.7 este dovedită.

Conform teoremei 26.7 (Sokhotsky), în orice vecinătate perforată (arbitrar de mică) a unui punct esențial singular, funcția /(r) ia valori arbitrar apropiate de orice număr din planul complex extins C.

Pentru a studia puncte singulare izolate, expansiunile Taylor deja cunoscute ale funcțiilor elementare de bază sunt adesea utile.

Exemplul 2G.8. Determinați tipul punctului singular zq = 0 pentru funcție

Rezolvat și e. Să extindem numărătorul și numitorul într-o serie de Taylor în puterile lui g zîn loc de r și scăderea 1, obținem

Folosind (22.12), obținem extinderea numitorului:

Serii din aceste expansiuni converg în întregul plan complex €. Avem

și /2(2) sunt anaritice într-o vecinătate a punctului zo = 0 (și chiar în întregul plan) și /2(20) F 0, atunci h(z) este, de asemenea, analitic într-o apropiere a punctului gF 0. Conform Corolarului 26.4, punctul Zo = 0 este polul ordinii N=4.

II Exemplul 26.9. Găsiți puncte singulare ale unei funcții f(z)= sin j - și determinați tipul lor.

R e in e i e Funcția are un singur punct singular finit zq = 1. În alte puncte din C funcţia w =--- analitic; de unde funcţia sin w va fi analitic.

Înlocuind în expansiunea sinusului (22.12) - în loc de r, obținem

Am obținut o expansiune a funcției sin într-o serie Laurent într-o vecinătate perforată a punctului 2o = 1. Deoarece expansiunea rezultată conține infiniti termeni cu puteri negative (r - 1), atunci zq = 1 este un punct esențial singular (în acest caz, expansiunea Laurent constă numai din partea principală, iar partea obișnuită lipsește).

Rețineți că a fost posibilă stabilirea naturii singularității în acest caz direct din definiție, fără a recurge la extinderea seriei. Într-adevăr, există secvențe (r",) și (2") care converg către zo= 1 și astfel încât f(z"n)= 1, /(2") = 0 (indicați singur astfel de secvențe). Deci, f(z) nu are limită la z -> 1 și deci punctul zq - 1 este în esență special.

Să introducem conceptul de expansiune Laurent a unei funcții în vecinătatea unui punct Zq = 00 și luați în considerare legătura dintre expansiune și natura singularității în acest punct. Rețineți că definițiile unui punct singular izolat și tipul acestuia (detașabil, pol sau, în esență, singular) sunt transferate la caz zq = oc fără modificări. Dar teoremele 26.2. 26.3 și 26.6, legate de natura expansiunilor Laurent, trebuie modificate. Ideea este că membrii cn(z- 2o) p. n= -1,-2,..., partea principală, care definește „neregularitatea” funcției în apropierea punctului final Zq, deoarece 2 tinde să oo, se vor comporta „corect” (tinde spre 0). Dimpotrivă, membrii părții corecte cu n= 1,2,... va tinde spre oo; ele determină natura caracteristicii în Zq = oo. Prin urmare, partea principală a expansiunii în vecinătatea oo va consta din termeni cu puteri pozitive p, iar cea corectă – cu cele negative.

Să introducem o nouă variabilă w = 1/2. Funcţie tv = 1/2, extins astfel încât u(oo) = 0, unu-la-unu și mapează conform vecinătății z > R puncte zq = 00 în vecinătatea |w| wq = 0. Dacă funcţia f(z) analitice în cartierul perforat R z Zq = oc, apoi funcția G(w) = f(l/w) va fi analitic în cartierul mare 0 wo = 0. Deoarece la 2 -> oo va fi w-> 0, atunci

De aceea G(w) are la un moment dat wq = 0 este o caracteristică de același tip ca f(z) la punct Zq = 00. Să extindem funcția G(w) într-o serie Laurent într-o vecinătate perforată a punctului wo = 0:

Sumele din partea dreaptă a lui (26.5) reprezintă părțile regulate și, respectiv, principale ale expansiunii. Să trecem la variabilă z, substituind w = 1/z:

Desemnarea n= -A*, 6* = 6_„ = s pși observând că G(l/z) = f(z), primim

Descompunerea (2G.G) se numește Expansiunea Laurent a funcției f(z) într-o vecinătate perforată a punctului zq= oo. Prima sumă din (2G.6) este numită partea dreaptă, iar a doua sumă este parte principală a acestei descompunere. Deoarece aceste sume corespund părților corecte și principale ale expansiunii (26.5), atunci analogii teoremelor 26.2, 26.3 și 26.6 sunt validi pentru extindere (26.6). Astfel, următoarea teoremă va fi un analog al teoremei 26.2.

Teorema 26.10. Punct singular izolatZq - OS (funcții/(G) este detașabil dacă și numai dacă expansiunea Laurent într-o vecinătate perforată a acestui punct are forma

c.t. constă doar din partea corectă.

Să punem /(oo) = co. Funcție definită de seria (26.7) convergentă în vecinătate z > R punctul 2o = oc, numit analitic la punctul z o = oo. (Rețineți că această definiție este echivalentă cu analiticitatea funcției G(w) la un moment dat wo = 0.)

Exemplul 26.11. Investigați punctul singular zq = oo al funcției

Din moment ce limita este finită, atunci zo = oo este un punct singular detașabil al funcției /(r). Dacă punem /(oo) = lim J(z)= 0, atunci f(z) va deveni analitic

tic la punct Zo= os. Să indicăm cum să găsim expansiunea corespunzătoare (26.7). Să trecem la variabilă w = 1 fz.Înlocuind z= 1 /?е, obținem

(ultima egalitate este valabilă într-o vecinătate perforată a punctului wо = 0, dar vom defini în continuare (7(0) = 0). Funcția rezultată are puncte singulare w =±i, w =-1/3, iar la punct Wq = 0 este analitic. Funcția de desfășurare G(w) treptat w(cum s-a făcut în exemplul 25.7) și înlocuind în seria de puteri rezultată w = 1/z, putem obține expansiunea (26.7) a funcției f(z).

Teorema 26.3 pentru caz zo= oo va fi rescris în forma următoare.

Teorema 26.12. Punct singular izolat th = os funcția f(z) este un pol dacă și numai dacă partea principală a expansiunii Laurent (26.6) are doar un număr finit de coeficienți nenuli Cu":

Aici seria este partea obișnuită, iar polinomul dintre paranteze este partea principală a expansiunii. Multiplicitatea polilor în oc este definită ca multiplicitatea polilor wq = 0 funcții G(z). Este ușor de observat că multiplicitatea polului coincide cu numărul Nîn (26,8).

Q p | (i 2 + 1)(z+3) 2

Sarcină. Arată că funcția f(z) =-- -- are in

punct zo = oo polul de ordine 3.

Teorema 26.6 asupra unui punct esențial singular poate fi rescrisă pentru acest caz zo= os aproape textual și nu ne oprim asupra acestui lucru în detaliu.